工程中模态灵敏度的计算方法

　　灵敏度即求导信息，它是一种度量，是一种评价由于设计变量或参数的改变而引起结构特性变化的变化程度的方法。系统的灵敏度分析的主要目的是确定设计参数变更时，系统响应、特征值及特征向量等发生的变化率，因此通过灵敏度分析可得到为实现最优化所需要的设计导数。它是当前力学和结构工程领域的主要研究方向之一。例如在结构优化、可靠性评估及结构控制等工程领域，灵敏度信息即是一个主要的先决条件，通常依据灵敏度性态来确定对优化目标及状态变量影响较大的设计参数，利用程序可自动选择灵敏度高的参数进行操作。在结构系统的模型修正时，基于设计参数及矩阵元素的修正算法，可以使用无阻尼实模态的正交归一化条件作为约束求解修正量，目前也有一些文献在使用复模态的正交归一化条件来设计修正算法，这些算法经常使用各种模态参数的灵敏度信息参与修正量的求解。当前，结构安全性检测有时也依赖灵敏度信息来确定结构是否出现损伤、损伤的位置及损伤的严重程度等。

　　1 阻尼与模态

　　依据结构阻尼的性质可将振动系统分为无阻尼、比例阻尼及一般粘性阻尼三种情况。在应用灵敏度分析的相关领域中，各种阻尼情况下的模态分析是其重要的基础。

　　无阻尼情况下的模态被称为实模态或纯模态，特征方程的根比较容易依据方程（λ2M+K）x=0的特征值问题求解，这种问题在数学意义上称为广义特征问题，得到实频率- ω2r=λ2r及相对应的实模态。当比例阻尼矩阵满足方程 C=αM+βK （α，β 为实常数） 时，比例阻尼系统具有复频率 λ2r，并满足【1】

　　
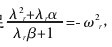
　　且与无阻尼系统具有相等的实模态向量。可见比例阻尼系统的数值计算量远低于一般的粘性阻尼系统。当系统的阻尼近似为一般粘性阻尼时，系统的极点与模态都是复值的，系统的特征问题为 （λ2M+λC+K）x=0。这不是一般意义上的特征问题，为了将系统特征问题转化为数学意义上的特征问题，即实值矩阵的一般特征问题，常将系统方程转入状态空间形式，第一种常见的状态方程形式为 Ay+By=0，其中 【2】

　　
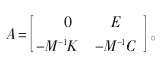
　　这种类型的状态矩阵总也不是对称的，导致它的右状态向量系总也不是内部正交的，还必须要求 M-1存在。但是，它的优点是振动系统的特征问题转化为一般矩阵 A 的特征问题，而不是第一种的广义特征问题。在使用两种状态方程的状态向量正交关系时，必须格外注意它们与系统的左右模态之间的关系，以及考虑系统性质矩阵是否对称等，否则极易得到错误的结论。讨论状态向量的正交性及灵敏度问题的意义在于2N 维状态向量的前 N 维恰为原振动系统的模态向量。

　　事实上，实模态在实际中是根本不存在的，而复模态从实验中是可以鉴别的。目前，在绝大多数利用特征问题灵敏度的结构分析领域中，如模态校正、损伤识别、设计优化、随机有限元理论等，还很少应用复模态分析，仅依赖于无阻尼实模态分析。我们在实际的实验性的模态分析中是可以识别复模态的。对于特征方程通常只考虑无阻尼的情形，即使必须面对阻尼特征问题时也只是假定在比例阻尼的情形下进行简单处理。这一方面由于在结构模型中能否适当地模拟阻尼是个问题，另一方面由于目前复特征问题的灵敏度分析方法还处于不够实用的阶段，因此开发针对复特征值与复特征向量的灵敏度分析的应用算法，是有实践意义和理论价值的。

　　在一般的非比例粘性阻尼面前，模态坐标下的运动方程可以通过模态和阻尼矩阵的非对角化条件进行解耦，当然此时结构模态和基频一般也是复值的。在此过程中，将产生两条技术线路，一个是在 N 维空间中的近似解法，一个是2N 维空间中的状态空间法，但当问题的容量加大时，状态空间法将付出数学方面的巨大努力，不仅如此，这种方法也缺少传统的模态分析中那种简朴的物理意义。以上原因导致必须在 N 维空间中进行一些深入的研究去分析非比例阻尼的模态灵敏度等情况。绝大多数的方法是寻求一些优化解法，或者仅仅忽略模态阻尼矩阵非对角化条件，也可以这样说，沿着这些方法论思考时模态仍然是实值的。不仅如此，除了假设低阻尼的前提下，这些方法的精确性还依赖于多种因素，例如模态间的频率分隔区间和主动频率等等。当然在实际中，为了能使用无阻尼实模态理论，常常在分析中合并复模态。

　　近几年，随着对阻尼系统的深入研究，研究者们开始把阻尼系统细化为经典阻尼及非经典阻尼系统，认为当系统的阻尼矩阵可以被系统的刚度和质量矩阵对角化，即模态阻尼阵为对角矩阵时，这个系统称为经典阻尼系统，否则称为非经典阻尼系统。对非经典阻尼系统各种振动分析已取得一定的进展，可参见文献。

　　2 无阻尼系统的模态灵敏度算法

　　综合近30年来的研究成果，可把模态灵敏度分析的方法分为两大类：直接法 （代数法） 和各种模态展开法。直接法是对特征方程求导后，通过支配方程的系数矩阵的非奇异化处理算法，来直接求解灵敏度的方法。而模态法是指对支配方程中的灵敏度作全模态线性展开，用各种模态的正交及规范化条件求得展开式系数的一类方法。Nelson基于Fox的方法首先提出直接法，对支配方程的系数矩阵 （K0- λ0iM0） 施行消行消列使其非奇异，进而求解灵敏度。因为它只须知道被分析模态的信息，故对于只涉及少数几个模态摄动的大型问题，它是有效的方法。随后直接法有了很多的发展，它们可用于保守系统、陀螺系统及一般系统的重特征分析。近年来模态展开法也成为人们研究的热点，文献[11]提出了经典模态展开法，用完备模态集的线性组合，通过求解组合系数来表示模态灵敏度。然后分别形成了修正模态法、迭代模态法、移位迭代模态法、幂级数展开法和混合基展开法等改进算法。所有这些方法都属于无阻尼振动系统的模态灵敏度分析算法。

　　3 阻尼系统的特征灵敏度分析算法

　　除了上文中对阻尼系统的分类方法外，还有一些分类方法，例如按系统性质矩阵的对称与非对称性分类，或按特征值的性态分为单频、重频及密频系统，再者模态系特点分为完备及亏损两种情况等。在具体的应用过程中由于系统的复杂性，这些分类方法可能存在多种形式的交叉。

　　在许多动力问题中，惯性、刚度和阻尼性质不能被对称阵或自连接的微分算子所表达，这种典型问题出现在主动控制结构中和许多非保守动力系统。例如，路上移动的汽车、按轨迹飞行的导弹、海上船体的运动和飘浮在空中的飞行器等。阻尼和刚度阵的非对称性经常在陀螺和随动力系统中出现。对大量的非对称系统，许多学者已经发展了Fox和Kapoor的方法来决定单频及重频阻尼系统的特征灵敏度。

　　Sondipon和Friswell在假定系统频率全不相同的 （单频） 情况下，对线性非对称系统的模态灵敏度给出了表达式，在理论上取得了很大进步。不过，他们虽然对伴有重频的保守系统的灵敏度给予一定程度的考虑，但对非比例阻尼系统中阻尼阵的某一单元秩变化后所产生的重频现象及其灵敏度分析却表示困难。

　　Lee等基于对称阻尼系统单、重频模态的灵敏度分别作出了论述。Kang- Min Choi等给出了对称重频阻尼系统模态的一阶乃至高阶灵敏度的计算方法。到目前为止，对非对称、密集模态灵敏度的研究仍是一个亟待开展的课题。

　　目前，在国内对非对称阻尼系统的重特征导数的研究方面呈现两种态势。一方面是对纯矩阵广义特征问题的重频模态灵敏度的研究，理论上作了大量分析，只是并未与振动二阶系统相联系，所以与工程实际中大规模应用尚有一定的距离；另一方面的研究是从状态空间形式出发开展严谨的讨论，使用全模态推导出 N 维空间中近似计算特征向量导数的方法，但有时推导过程及结论较为繁琐，不宜于一般工程人员理解和使用。总之，对于大型工程问题发展适用的模态灵敏度分析方法仍然十分必要。

　　在很多结构系统中即使出现密频或重频的问题，在讨论中一般都假定系统为完备系统来分析模态灵敏度。但在亏损振动系统，这个过程的研究发生了困难，如非比例阻尼矩阵，或在非保守力作用下的结构动力问题，气动弹性颤振分析，以及结构和控制系统相耦合的问题，其有关的矩阵可能是亏损的。事实上，当非经典阻尼系统的非经典模态对应的频率的几何重数小于其代数重数时，就必定会出现亏损系统的特征问题。许多流固耦合动力学问题、自动控制问题中会遇到亏损频率问题。Luongo甚至构造出一族两自由度亏损系统。张慧生等提出了一般矩阵的亏损特征对的摄动方法，却不属于灵敏度分析方法的范畴。文献[25]从亏损系统的特征问题出发，利用广义模态理论建立亏损系统广义模态向量系进行模态灵敏度的分析，以实现系统的优化与控制，但该方法没有唯一地确定模态灵敏度的展开式系数。因为对亏损系统的认识和研究仍然处于发展阶段，所以较为成熟及操作性强的灵敏度分析方法仍亟待开发。

　　[参 考 文 献]

　　[1]Querin OM,YoungV,Steven GP,et al. Computational efficiencyand validation ofbi- directional evolutionarystructural optimization[J].Computer Methods in Applied Mechanics and Engineering,2000,189:559- 573.
　　[2]何建军,姜节胜.基于降阶模型的非经典阻尼结构拓扑修改的复模态重分析方法[J].振动与冲击,2009,28(7):50- 54.
　　[3]赵红兵,孙国,顾元宪.采用新型损伤指示因子和结构优化方法的单元损伤识别[J].计算力学学报,2006,23(5):573- 576.
　　[4]张淼,陈庆文.两种常见的状态方程及其特征向量的正交性[J].长春工程学院学报:自然科学版,2011,12(2):122- 125.
　　[5]Z.S.Liu,D.T.Song,C.Huang.Vibration Analysis ofNon- ClassicallyDamped Linear Systems[J].ASME Journal ofVibration and Acou-stics,2004,126:456- 458.
　　[6]于澜,张淼.简谐激励下非经典阻尼系统的稳态响应[J].长春工程学院学报:自然科学版,2011,12(2):126- 128.