从谓词抽象角度考察“相等”难题

　　一、 弗雷格的 “相等” 难题

　　弗雷格在 《论涵义和意谓》 中谈到了 “相等” 问题。 主要讨论两种相等， 一是名称的相等， 二是句子的相等。 该文章开篇写道：

　　由于相等涉及许多问题……它是一种关系么？ 一种对象之间的关系？ 还是对象的名字或符号之间的关系？ ……a=a 是先验有效的， 根据康德， 应该叫分析的， 而具有 a=b 形式的句子常常十分有意义地扩展了我们的认识， 并不能先验地建立起来…… 如果我们现在把相等看成是 “a” 和 “b” 名字意谓的东西之间的关系， 那么看来， 如果 a=b 真， 则 a=b 和 a=a 就不能是不同的……a=b 要表达的似乎是 “a”和 “b” 这两个符号或名字意谓相同的事物， 因此恰恰是这些符号； 也陈述了这些符号之间的关系……显然， 与一个符号 （名称， 词组， 文字符号） 相关联， 除要考虑被表达的事物， 即可称为符号的意谓的东西外， 还要考虑那种我们要称为符号的涵义的， 其间包含着给定方式的东西。

　　弗雷格在这段文字里表明， 两个名称相等， 不仅仅说名称的意谓 （也有人译为指称或所指） 相同， 还要考虑名称的涵义。 a=b 真， 则 a、 b 指称对象相同， 但 a 和 b 的涵义不同。 名称有意谓和涵义， 句子也有涵义和意谓。 弗雷格认为， 句子的意谓是它的真值 （真和假）， 涵义是其表达的思想。 两个句子相等是说它们意谓相同， 而它们表达的思想不同。 例如 a=b 和 a=a 两个句子， 两个句子的真值相同， 但涵义不同。 a=a 表达了一个不足道的先验知识， 而 a=b 则表达了后验知识。

　　对于有些名称来说， 涵义是清楚的， 但其意谓却不好确定。 如 “最小的收敛级数” 关于其意谓是什么，并无定论， 弗雷格认为这个名称是没有意谓的， 这就是名称有涵义无意谓的情况， 即空词项。 与名称相类似， 句子在间接语境、 从句或其他语境， 比如认知词、 相信或模态语境中， 句子的意谓发生了变化。 在间接语境下， 句子无通常意谓， 只有间接意谓， 而其间接意谓是其通常的涵义。 复句中的分句在从句或其他语境中通常也没有直接意谓， 只有涵义， 而其间接意谓是思想且是复句思想的一部分。 在这些情况下， 莱布尼茨律即同一保真替换不成立， 所谓同一保真替换指： “给定一个关于同一性的真陈述， 可以用它的两个词项中的一个替换另一个出现在任一个真陈述中的词项， 而其结果将是真的”。

　　相等在外延语境中是不成问题的， 经典一阶逻辑已经显示了这一事实。 但正如弗雷格所注意到的， 相等在其他语境中， 比如内涵语境中， 并不一定成立， 而这正是造成人们困惑的地方。 现代逻辑意义上的内涵语境包括认知、 信念和模态等情况， 这远远地超出了弗雷格所理解的范围， 内涵语境的典型形式是模态语境，所以， 我们下面的讨论主要针对模态逻辑而言。 在模态语境中， 若用 “□” 表示 “必然”， 则 “相等” 难题的一个重要问题可用公式表示为：

　　1. x=y →□（x = y）

　　上述公式在模态逻辑中成立么？ 弗雷格没有把这个问题深入探究下去， 他也没有可能探究下去， 这是因为在弗雷格时代尚无模态逻辑理论。 但弗雷格旗帜鲜明地指出， 相等的两个词项在某些语境中不能保真替换， 这表明了走外延路线的经典逻辑的局限性， 我们还需要一些超出外延的内涵逻辑。

　　如上所述， 弗雷格的 “相等” 问题涉及如下几个方面内容。 第一， 什么东西相等， 这种相等是否具有必然性？ 它们涉及涵义和指称。 第二， 相等能否在所有语境中保持？ 进一步而言， 在内涵语境中是否可以同一保真替换？ 第三， 在词项只有涵义没有意谓的情况下， 如何看待词项的相等及其相关命题的真假？ 这涉及空词项问题。 我们把这些关于相等难题统称为 “弗雷格之谜”。

　　二、 谓词抽象和从言、 从物模态。

　　弗雷格的 “相等” 难题一直得不到较好解答， 是因为经典逻辑是一种外延逻辑， 逻辑外延化的倾向影响巨大， 以至于后来发展的模态谓词逻辑依然带有外延化的倾向， 所以， 它不能很好地处理弗雷格所提出的问题。 一个熟悉的例子是：

　　2. 晨星等于暮星。

　　按照弗雷格的理论， 该句中这两个名称的指称对象相同， 但涵义不同。 指称对象是外延的， 而涵义则是内涵的东西。 从语形层面看， 若要用形式语言完整地表达这个命题的意思， 则相关的公式既要体现出外延， 又要体现出内涵。 从语义层面看， 名称的指称比较好办， 在模型的论域里直接指定一个对象即可。 而名称的涵义， 按照摹状词理论，[3]

　　涵义是确定一个名称对象的方式， 而这是不好刻画的。 关于内涵语义， 影响最大的是克里普克的可能世界语义学， 尤其值得一提的是克里普克在其着作 《命名和必然性》 中， 用严格和非严格指示词表达名称的不同的指称方式。 “如果一个指示词在每一可能世界中都指称同一个对象， 我们就称为严格指示词， 否则就称为非严格的或偶然的指示词”。[4]

　　例如， “行星的数目” 是非严格指示词， 而 “9” 则为严格指示词。 但是在克里普克的系统里， 这两者的区分是事先给定的， 并且是在语义层面给定的区别。 在语形层面， 从一个模态公式里我们看不出一个词项是严格指示词还是非严格指示词。 究其原因， 克里普克缺乏一个有效区分外延和内涵的逻辑工具。

　　在模态逻辑范围内， 若要回答弗雷格 “相等” 难题， 必须要同时从外延和内涵两方面着手， 单方面的解决方式是难以奏效的。 在模态逻辑中， 涉及内涵概念的除可能世界概念外， 还包括从言、 从物模态的区分，甚至包括严格指示词和非严格指示词的区分。 通常所讲的从言、 从物模态区分是针对包含量词的这类特殊的模态公式而言， 例如：

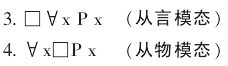
　　但是， 包含量词的模态公式只是一类特殊的公式， 不具有普遍性， 对不含量词的一般公式， 例如：

　　5. 行星的数目必然大于 7。

　　这个句子的从言、 从物模态就不好用公式表达了。 若用 τ 表示 “行星的数目”， b 表示 “7”， ＞表示大于关系， 则上面这个句子表示为：

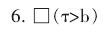
　　对于这个句子， 我们无法在模态谓词逻辑的形式语言中刻画其从言模态和从物模态。 但在日常语言中， 我们认为 “行星数目” 的意谓是 “9”， 并对句 5 有两种理解方式， 即：

　　7． 行星数目大于 7， 这是必然的。

　　和8． 行星的数目 （也就是 9） 必然大于 7。

　　前一种理解着重于命题 “某事物具有属性 P” 是必然的。 后一种理解着重于某个特定事物， 该事物必然具有属性 P 。 前面一种理解偏重于命题的必然性， 后一种理解偏重于事物的必然性， 我们称前一种为从言模态，后一种为从物模态。 但是， 公式 6 无法体现出这一点， 从言、 从物模态的表述在这里遇到了困难。 对于公式6， 需要用一个恰当的方法把词项 τ 的从言、 从物形式区别开来。

　　菲汀 （M. C. Fitting） 对谓词抽象做了比较深入的研究， 其研究成果为我们提供了一个很好的技术平台。[5]

　　谓词抽象理论的出现， 才使得我们有一个工具表达一个词项究竟是侧重于词项指称的对象 （即从物模态）还是侧重于词项的指称方式 （即从言模态）， 并且可以在不含量词的普通公式中得到体现。 先引入一个新的符号λ， 称为抽象谓词， 这是一个特殊的谓词。 在新的模态形式语言中， 运用抽象谓词， 把句 6 中的词项 τ的从物模态表示为：

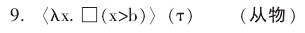
　　而把句 6 中的词项 τ 的从言模态表示为：

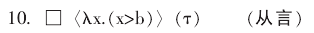
　　另一方面， 对于名称的指称方式， 也就是涵义， 这是语义层面的东西。 对于句子 5 中的 “行星的数目”，做从物理解则先考虑名称的指称即 9， 再考虑该对象 9 在不同可能世界中具有什么属性。 对 “行星的数目”

　　做从言理解， 则先考虑该词项指称的方式变化情况。 换句话说， 在模态语境中该名称的指称对象可能是 9，也可能是其他对象， 在这之后， 再考虑该词项所指称的对象具有什么属性。 这种考察的先后顺序对于模态从言和从物的区分是重要的， 它是谓词抽象理论的一个重要的语义特点。 依据菲汀谓词抽象理论， 谓词抽象语义的主要思想在于通过一个变元与一个常元绑定， 变元的指派不受其模态词的影响， 在从物模态中， 某个变元先绑定一个常元， 再考虑其在可能世界中的属性变化； 在从言模态中， 先考虑可能世界， 再考虑与常元绑定， 然后考虑属性， 通过这样的方式来区别从言和从物模态。[6]

　　简言之， 就是把常元 τ 的指派过渡到一个变元 x 的指派。 在从物模态情况下， 即句 9， 首先考虑此词项指称的对象 “d” （这个 d 即对象 9）， 一个模型 M和赋值 V 在可能世界 w 中使得 V（τ）w 为 9。 考虑类似公式□（x>b） 的赋值， 使得 V（d/x）（□（x>b））w=1。 在这里， 令 V（d/x）（x）w =V（τ）w ， 由于在同一个模型 M 中， 指派 σ 对同一个变元的指派是不变的， 我们可简写为 V（d/x）（x）=V（τ）w。 据代入引理， 这两个公式在模型 M 中的取值是相同的。 在与 w 的所有可通达世界v 中， 若 V（b）v 为 7 ， 显然 9 大于 7， 即 V（d/x）（x> b）v =V（x>b）v=1。 在这里， 句 9 的 赋值为真 。 在从言模态的情况下， 即句 10 （τ 在现实世界指称 9， 但在另一可能世界可能指称 6）， 首先考虑的是模态词， 考虑类似公式□（x>b） 的赋值， 使得 V（d/x）（□（x>b））w=0。 在与 w 的所有可通达世界 v 中， 若 V（b）v 为 7 ， 令 V（x）= V（d/x）（x） =V（τ）v ， 且 V（τ）v 为 6， 显然 6 小于 7， 即 V（d/x）（x>b）v =V（x>b）v=0。 据 代入引理 ， 我们容易知道 V（d / x）（□（x>b））w=V（□（x>b））w=0。 在这里， 句 10 赋值为假。

　　可见， 谓词抽象在语形和语义层面都可以很好地刻画模态从言和从物形态， 使得模态语言表达能力更强。 它还可以结合可能世界对涵义做更细致的处理。 下面用谓词抽象理论来分析弗雷格 “相等” 难题的三个方面。

　　三、 从谓词抽象角度考察 “相等” 难题

　　首先用谓词抽象理论来分析名称相等的必然性问题。 对于句 2 即 “晨星等于暮星” 这个命题， 若我们的理解侧重于名称的意谓相同， 用从物命题表达即可； 若侧重于指称方式， 即涵义不同而意谓相同， 用从言命题表达即可。 现在， 我们用 τ 表示 “晨星”， 用 ξ 表示 “9” （τ 和 ξ 表示非严格指示词）， 则句子 2 的谓词抽象形态可以有如下几种：

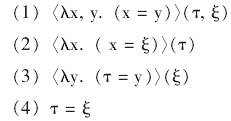
　　其中， （1） τ, ξ 均为从物状态， （2） 中 τ 为从物状态， ξ 为从言状态， （3） 两者恰好与 （2） 相反， （4） 为一般形态， 我们默认为是从言状态。 引入谓词抽象是为了区别内涵语境中从言和从物公式， 在外延语境中， 从言和从物的区别意义不大。 一旦进入内涵语境， 这种差别的意义就凸现出来了。 古人都知道晨星是晨星， 也知道暮星是暮星， 但可能不知道晨星是暮星。 对于前两者， 古人知道任何一个对象都等于它自身这个道理，对于第三者， 古人不知道 “晨星” 这个名称指称的对象和 “暮星” 这个名称指称的对象是同一个事物。 发现晨星是暮星是一个天文学的发现。 现代人说古人不知道 “晨星是暮星” 时， 显然是对这个句子作从言理解。

　　在这里， “知道” 表示为 “□”， 句子 2 用谓词抽象可表示为两个公式：

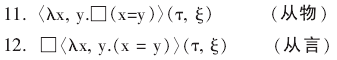
　　从物公式 11 表达的意思是两个名称所代表的对象同一， 说古人不知道这个道理， 这是有悖直觉的， 古人也不会做如此理解。 在这种情况下， 公式 11 表达是对象自身相等， 这种同一或相等是不随可能世界改变而改变的， 因而， 公式 11 是成立的。

　　从言公式 12 表达的意思是相等的名称指称方式在某个可能世界是同一的， 说古人不知道 “晨星” 和“暮星” 的指称方式相同， 这是符合直觉的。 两个名称相等， 并不代表它们的意谓在所有其他情况下都相同，它们的意谓随着可能世界的变化而变化， 因而， 公式 12 不成立。

　　再回到句 1， 即 “x=y→□ （x=y）” 是否在模态逻辑中成立的问题。 引入谓词抽象， 句 1 则有两种表现方式， 一个是从言方式， 一个是从物方式。 若用 t1和 t2表示两个项 （项 t1, t2指常元， 不一定为严格指示词， 也可以为非严格指示词）， 则分别表示为：

　　其中 x 和 y， 是变元， 可由常元进行替换。 已经知道， 模态谓词逻辑关于相等有两种系统， 一个是必然等同系统， 另一是偶然等同系统。 必然等同系统认为两个事物相等则必然相等， 即自身同一具有必然性； 另一个认为是两个事物相等但并不必然相等， 即自身同一不具有必然性。 那么， 句 1 所表达的关于相等的必然性可分析为如下几种情况。 第一， 在必然等同系统中， 句 1 的从物方式即公式 14 成立。 句 1 的从言方式即公式13 还需要具体分析： 一方面， 若句 1 中等项涉及的是严格指示词， 由于严格指示词对谓词抽象不敏感， 其从言句式和从物句式等价，[7]因而公式 13 依然成立； 另一方面， 若句 1 中等项涉及的是非严格指示词， 则句 13不成立。 第二， 在偶然等同系统中， 这两个式子都不成立， 根本就排除了相等问题的讨论， 彻底回避了弗雷格相等难题， 当然这种面对难题的方式是不能令人满意的。

　　可见， 关于两个词项相等， 若认为是两个词项的涵义相等， 可用谓词抽象表达为从言形态， 在内涵语境中， 这种相等不具备必然性； 若认为是两个词项的意谓相等， 可表达为从物形态， 在内涵语境中， 这种相等具有必然性。 这两种情况在引入谓词抽象后， 都可以在逻辑上得到合适的处理， 产生困惑的根源在于弗雷格对内涵语境中的相等偏重于从言理解， 而忽略从物理解。 弗雷格提出涵义与意谓之分， 在哲学上给人诸多启发， 但也容易给人一种错觉， 那就是涵义和意谓似乎在逻辑中可以截然区分开来。 涵义即指称方式， 属于内涵， 反之， 意谓属于外延。 在传统模态逻辑中， 在语形层面， 勉强用量词和模态词结合来区分模态从言和从物状态， 这样， 完全看不出公式内涵和外延的区别； 在语义层面， 比如可能世界语义学， 仅仅用可能世界来表达内涵的东西， 这是不充分的。 这种截然二分的方式， 始终难以精确弗雷格关于名称相等的疑问。 通过谓词抽象分析发现， 在语形层面， 从言公式偏重指称方式， 这有内涵的意味， 从物公式偏重指称的对象， 这有外延的意味； 在语义层面， 通过谓词抽象可直接穿透可能世界， 与可能世界配合可更灵活地在外延和内涵之间转换。 因而， 抽象谓词本身是一个兼带内涵和外延意义的逻辑工具， 它表明内涵和外延在逻辑上并不是截然二分的东西。

　　接下来探讨内涵语境中同一保真替换有效性问题。 这涉及命题的真值相等， 弗雷格认为命题的涵义是思想， 意谓是真值， 真值相同的命题在直接语境中可以保真替换， 但在间接语境中， 由于命题不具有通常的意谓， 所以不能保真替换。 我们同样从外延和内涵两方面着手方探究这个难题， 依然只考虑模态语境这一情况。 例如：

　　15. 9 必然大于 7

    若要遵循弗雷格的本意， 我们只能认为这个句子所表达的命题 “9 大于 7” 是必然的， 这显然是一种典型从言模态理解方式。 针对名称 “9”， 却可以有从言和从物两种理解方式， 即：

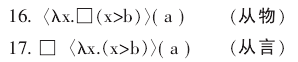
　　但是由于 “9” 是严格指示词， 其意谓不随可能世界改变而改变， 这两个公式都为真， 可以证明这两个公式是等效的。 这说明， 谓词抽象对严格指示词是不敏感的。 已经知道句 5 “行星数目必然大于 7” 同样有两种理解方式。 考虑到 “行星数目等于 9”， 对句 15 进行替换可得到句 5， 则有如下情况。 第一种是对句 15 的从物形式句 16 进行替换， 得到从物句 9， 我们把这种替换称为从物替换， 从真前提得到了真结论， 这种替换是没有问题的。 第二种是对句 15 的从物形式句 16 进行替换， 得到从言形式句 10， 我们把这种替换称为从言替换， 从真前提得到了假结论， 这种替换是不保真的。 但若句 5 中等项涉及的是严格指示词， 这种替换依然是保真的。 第三种是对句 15 的从言形式句 17 进行替换， 得到从物形式句 9， 从真前提得到了真结论 ， 这种替换是没有问题的。 第四种是对句 15 的从言形式句 17 进行替换， 得到从言形式句 10， 从真前提得到了假结论， 这种替换是不保真的。 但若句 5 中等项涉及的是严格指示词， 这种替换依然是保真的。

　　对上述情况进行归纳， 则同一替换中需要考虑的因素有两方面。 第一， 替换词项是否为严格指示词。 若替换词项为严格指示词， 则模态语境下同一替换是保真的。 严格指示词和非严格指示词的区分主要在于词项的指称方式不一样， 可见指称概念不仅仅是个外延概念， 还是一个重要的语义概念， 这又说明了在逻辑中，外延和内涵不是截然二分的。 第二， 进行替换的方式也是一个需要考虑的因素， 从物替换或从言替换所得到的结果是不一样的。 所有模态语境下的从物替换都是保真的， 对于从言替换， 若替换词是严格指示词， 则该替换也是保真的。

　　由此可知， 同一保真替换在内涵语境中， 并非是不成立的， 若处理为从物替换， 即使是在内涵语境中，也是可保真替换的。 从言替换在内涵语境中， 可能不成立， 但若其词项涉及的是严格指示词， 则从言替换也是成立的。 弗雷格乃至后来受弗雷格所影响的人， 包括蒯因， 都把同一替换问题简单化了。[8]对于同一保真替换， 需要考虑内涵语境这一个因素， 还需要区分从言和从物命题， 注意词项的指称方式， 包括严格指示词和非严格指示词的区别， 而不能笼统地说， 模态命题中的同一是不能保真替换的。

　　弗雷格还提到， 有些名称只有涵义没有意谓， 例如 “孙悟空” 这些词项， 我们称为空词项。 引入空词项之后， 使得相等问题更为复杂。 例如， 用 a 表示名称 “齐天大圣”， b 表示名称 “孙悟空”， 按照弗雷格的理论， a=b 还是一个真句子么？ 弗雷格的立场比较模糊： 一是拒绝面对这个问题。 弗雷格下面这段话清楚地表达了他的这一立场： “逻辑完善的语言 （概念文字） 应该满足下列条件： 由已经引入的符号作为专名而合乎语法规则的构造起来的每一个表达式， 实际上也表示一个对象， 并且一个符号的意谓若不确定， 这个符号就不能作为一个专名引入”。二是即不肯定也不否定， 弗雷格举了一个例子： “奥德赛在沉睡中被放到伊萨卡的岸上”。“奥德赛” 是荷马史诗中一个人物， 可能不存在， 弗雷格认为这个句子只有涵义而无意谓， 即这个句子没有真值。 这个思想后被施特劳森加以阐发， 即着名的语义预设理论。显然， 若 a 是 “齐天大圣”，b 是 “孙悟空”， 按照弗雷格第二种观点， a=b 是一个无法判断真假的句子， 它有涵义但无真值。弗雷格第一种方案是一种釜底抽薪式的方法， 回避问题从来就不是一个好建议， 第二种方案则超出了经典二值逻辑的范围。 对于空词项情况下 “相等” 难题， 弗雷格也没有提出让人满意的方案。 这将要牵涉四个因素： 涵义、 意谓、 语境、 空词项。 经典一阶逻辑是不处理空词项的， 但包含空词项的推理大量地存在于我们日常生活中， 而这恰是一阶逻辑和以一阶逻辑为基础的模态谓词逻辑的短板。自由逻辑是一种处理空词项的逻辑， 在自由逻辑的基础上加入模态算子可构成自由模态逻辑。自由模态逻辑可涵盖上述四个因素，最有可能对包含空词项的 “相等” 问题做出合理解答， 我们应该把关于空词项相等的问题所讨论的范围转移到自由模态逻辑当中去。 对于空词项 a 和等式 a=b， 与经典逻辑束手无策相比， 自由模态逻辑可有多种选择，既可以放到正自由模态逻辑里去分析， 也可以放到负自由或中性自由模态逻辑里去分析。 每一种选择都提供了一个系统的语形和语义框架， 进而可以对空词项及其相等做出相应的刻画。 限于篇幅， 此处就不再详细讨论。

　　四、 结语

    现在， 对 “相等” 难题的三个方面， 给出我们的回答如下。

    在模态语境里， 相对于模态谓词逻辑必然等同系统而言， 相等的必然性可分解为如下几种情况。 第一，专名相等， 视同为严格指示词相等， 无论其从言形式还是从物形式， 都是必然相等的。 第二， 摹状词相等，视同为非严格指示词相等， 这是弗雷格相等问题的主要困惑， 分为两种情况： 其从物形式是必然相等的； 其从言形式不是必然的。 第三， 变元的相等， 可划归严格指示词这种情况， 其相等是必然的。

　　弗雷格论及的同一保真替换， 在间接语境或内涵语境才会出问题。 这是因为既要考虑涵义还要考虑意谓， 而且其涵义和意谓还有可能会改变， 运用谓词抽象对之进行分析， 同一保真替换可分为三种情况。 第一， 在所有情况下， 从物替换是保真的。 第二， 若等项涉及严格指示词， 无论是从言替换还是从物替换都是保真的。 第三， 若等项涉及非严格指示词， 则从言替换不保真。

　　关于空词项及其相等的问题， 可以放到自由模态逻辑中加以考虑， 这同样需要谓词抽象这一工具。综上所述， 弗雷格 “相等” 谜题涉及涵义、 意谓、 语境几个因素。 谓词抽象在语形层面， 既可以表达包含量词的这一类特殊的模态公式的两种模态， 还可以表达不含量词的更一般的模态公式的两种模态， 从而加强了模态谓词逻辑形式语言的表达能力； 在语义层面， 它可以同时勾连指称方式， 并与可能世界兼容， 这进一步完善了克里普克的模态语义理论。 谓词抽象对诸如蕴涵、 否定等真值连接词不敏感， 但对模态词敏感，这一点正突出了谓词抽象在内涵逻辑中的重要作用。 引入谓词抽象这一工具， 可以穿透模态语境， 把涵义和意谓结合起来， 纠正外延和内涵截然二分这一错误倾向， 并对严格指示词和非严格指示词进行有效刻画。 这样， 关于 “相等” 问题的逻辑迷雾也就基本上消散了。

　　[参考文献]

　　[1][9][10] 弗雷格： 《弗雷格论着选辑》， 王路译， 北京： 商务印书馆， 2006 年， 第 95、 110、 102 页。

　　[2][8] 蒯因： 《从逻辑的观点看》， 陈启伟、 江天骥等译， 北京： 中国人 民 大学 出版社 ， 2007 年 ， 第 150、 151-156页。

　　[3] 罗素： 《逻辑与知识》， 北京： 商务印书馆， 1996 年， 第 49-68 页。

　　[4] 克里普克： 《命名和必然性》， 梅文译， 上海： 上海译文出版社， 1988 年， 第 49 页。

　　[5] M. C. Fitting， “First-Order Intensional Logic”， Annals of Pure and Applied Logic， 2004， vol.127， pp.171-193.

　　[6][7] M. C. Fitting and R. L. Mendelsohn， First-Order Modal Logic， Dordrecht: Kluwer， 1998， p.198， 212.

　　[11] P. F. Strawson， Introduction to Logic Theory， London： Routledge， 1952， p.175.

　　[12] 胡 泽洪 、 邓雄雁 ： 《论 模态 谓 词 逻辑 的 “非指 称 ” 问题──基 于 自 由 逻辑 的 考 察 》， 《哲学研究 》 2011 年 第 1期。

　　[13] J. Garson， Modal Logic for Philosophers， Cambridge： Cambridge University Press， 2006， p.245．