改进拉子群舞法的电力负荷预测模望

　　电力负荷预测论文第三篇：改进拉子群舞法的电力负荷预测模望

　　摘要：采用粒子群算法构建电力系统负荷模型，并利用支持向量机模型对电网负荷进行优化处理，以径向基函数作为支持向量机的核函数，以电力负荷作为输入量，建立基于改进粒子群优化算法的电力负荷预测模型。以居民小区为基本单位进行用电信息采集，采用改进粒子群算法对用电情况进行验证分析，并将改进粒子群电力负荷预测模型与支持向量机预测模型进行比较。结果表明：建立的基于改进粒子群优化算法电力负荷预测模型具备更高的预测精度与更好的适用性。

　　关键词:电力负荷;粒子群算法优化;建模;模型训练;

　　0 引言

　　随着社会和经济的飞速发展，能源需求量也在逐年递增，电力负荷的预测对于系统规划和合理运营电力资源有着重要的指导意义。

　　随着对电力负荷预测技术研究的不断深入，电力行业的各专家、学者针对不同的应用场景提出了相应的电力负荷预测方法。唐玮提出的基于GRA-LSSVM的配电网空间负荷预测方法中提出了一种基于最小二乘法支持向量机的新型配电网空间负荷密度的预测算法，这种采用混沌粒子群算法对参数进行优化选择，虽然提高了算法空间的负荷密度预测精度，但是此算法需要多个不同类型空间样本，且预测精度受自身参数影响较大[3];唐宏通过引进萤火虫算法，对SVR参数进行优化处理，然后利用优化SVR算法进行短时电力负荷预测[4];范海虹在萤火虫算法的基础上提出卡帕测度，构建预测模型函数，对短期电力负荷进行预测，萤火虫算法只能进行短期预测，且应用场景单一，泛化性能较低[5]。

　　为了提高电力预测的稳定性、适用性及便于推广性，本文在粒子群算法的基础上对引入的支持向量机模型参数进行训练，获得最优解，构建灵活稳定的电力负荷预测模型。

　　1 支持向量机原理

　　支持向量机的概念最早是由Corinna Cortes和Vapnik于1995年为解决小样本、非线性函数拟合问题而提出的，支持向量机理论完善且计算简单，又兼具较好的鲁棒性等，可为模式识别提供较好的泛化性能。本文引入SVM的数据学习能力，对电力负荷进行预测分析。

　　引进两个未知变量：x、y,其中，变量x为输入样本值，变量y为输出样本值。数据样本几何表示为(xi、yi),其中，输入样本集xi∈Rn,输出样本集yi∈R,R取实数域，i=1,2,…,n(n→+∞)。利用非线性映射关系完成样本数据x从低位空间到高位空间的转换，完成转换后，利用SVM的回归理论解决高维度空间的回归问题。可对预测模型进行建模处理，表达式为：

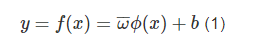
　　其中，ω??为权重；?(x)为低维度空间到高维度空间的非线性映射函数关系；b为偏置项，通常取值为某一常数。

　　对优化后的目标函数作求取极值处理，如式(2)所示：

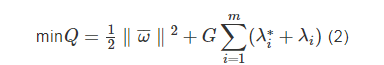
　　其边界条件为：

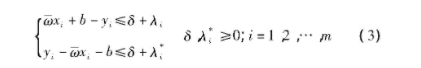
　　其中，G为惩罚因子，决定了预测模型函数的精准度和复杂程度；δ为损失函数，与预测模型函数的泛化程度相关；λi、λ*i为松弛因子。

　　引入拉格朗日乘子向量解决高维度空间的规划问题：

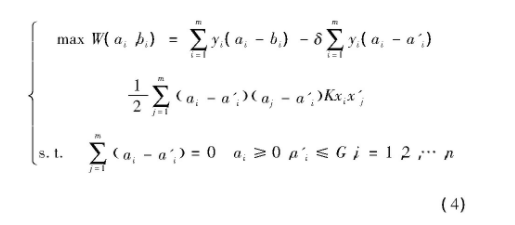
　　其中，i、j为整数，取值为1,2,…,m。ai、bi均为拉格朗日乘数因子，xi,j、yi对应输入、输出量。

　　利用核函数K(xi,xj)=?(xi)?(xj)可以完成对非线性样本数据从低维度到高维度的转换。考虑到泛化性能，本文选用适用性更好的径向基核函数K(xi,xj)=exp(?∥x?xi∥2)2g2,代入预测模型函数，得到SVM的决策函数表达式为：

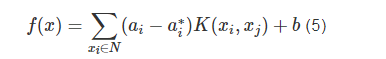
　　核函数确定后，还需要寻找出惩罚因子G及对应的核函数模型g,通过引进一种改进的粒子群算法来对SVM的参数G、g进行训练优化。

　　2 粒子群优化算法

　　2.1 粒子群优化算法原理

　　粒子群优化算法由美国学者Eberhart和Kennedy于20世纪90年代共同提出的，其原理是通过模拟鸟群觅食行为而产生的群体协作，且具有群集智能的多主体优化随机搜索算法，具体描述如下所示[6,7]:

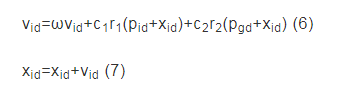
　　其中，xid为对应第i个粒子在d维空间的坐标值，vid为对应第i个粒子在d维空间的速率；pid对应第i个粒子在全局范围内搜索到的实时最优位置，pgd对应第i个粒子在全局范围内搜索到的种群最优坐标；ω为粒子群算法的惯性权重因子，对算法的寻优能力有着显着影响，ω在其定义域区间从最大值到最小值衰减取值，此取值方法可保障粒子杜绝早熟收敛的情况出现；c1、c2为学习因子，为了保证收敛速度和搜索效果均衡，依据经验可定义取值范围为c1,c2∈[1.85,2.25];r1、r2为相互独立的随机函数，取值范围为r1,r2∈[0,1]。

　　PSO算法在实际运用过程中可分为7步，逻辑时序图如图1所示。

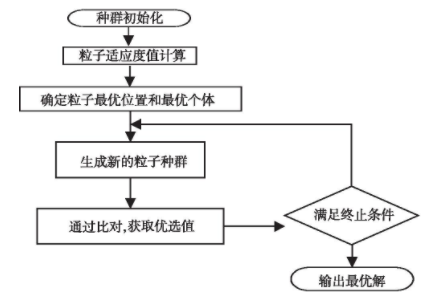
　　图1 PSO算法流程图 

　　2.2 改进粒子群优化算法原理

　　惯性权重因子ω具有影响算法寻优能力的作用，即当ω取值偏小时，全局搜索能力也随之减小，此时会出现搜索范围广度不够的情况，极有可能引导算法形成局部最优解；当ω取值较大时，收敛能力随之变差，导致算法无法形成最优解而陷入无限寻优计算的死循环中。为解决参数ω的功能局限性问题，特根据需要引入自适应惯性权重法[8,9,10]。该方法可根据实现应用场景，自行调整ω迭代时的变化速率，以提高寻优概率，公式表示如下：

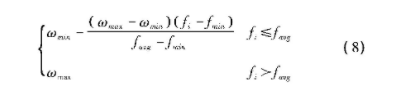
　　其中， fi为第i个粒子的当前迭代适应度值。

　　PSO算法在全局范围内搜索寻优过程中，随着时间的推移搜索速率会逐渐减慢，当遇到局部最优解便会停止搜索。此时，算法便会陷入局部极值问题，为了解决算法由于在最初时搜索速度过快而引起粒子搜索不均匀问题，引入粒距概念来解决此问题，粒距定义如下：

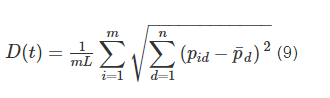
　　其中，D(t)为粒子间距，是粒子分散程度的直观体现，D(t)的数值越大，表示粒子分散成俗越高；n为空间维度；pid表示第i个粒子在第d维度的数值；p?d为全局范围内的所有粒子在d维度范围内的均值。

　　根据实际的应用场景对某一重点局部搜索的性能进行改进，用以避免在局部搜索时出现早熟收敛，造成出现局部最优解的情况。通过预先设定一个合理的初始阈值h, 并与粒距进行迭代比较，若比较得出粒距D(t)大于所选阈值，则无需对粒距做任何处理；若D(t)小于所选阈值，则对种群进行高斯变异处理，在[0.1,0.3]范围内，选择粒子，粒子变异前后须保证粒子的基础信息保持一致。

　　3 基于改进PSO-SVM负荷预测模型

　　本文以径向基函数作为支持向量机的核函数，以电力负荷作为输入量。通过改进的PSO-SVM的算法对参数进行优化具体流程如下。

　　1)种群初始化。初始化各项参数：种群大小m取值为15,惯性权重的最大值ωmax取值为1.2、最小值ωmin取值为0.4,学习因子c1、c2取值为2.05,根据经验预设变异值h取值9.8,变异概率pm取值为0.31。

　　2)完粒子适度值计算。

　　3)更新全局范围内的最优解pg及历史最优解pb,比较最优解与历史最优解，选取更优者作为当前值。

　　4)通过自适应模型计算出自适应惯性权重，完成当前惯性权重的更新，并更新粒子的速度和位置以获取新的种群X(t)。

　　5)变异判断。将粒距与设定的阈值比较，判断是否需要变异操作，若需要则执行高斯变异，确定粒子选择概率pm;若不需要变异操作则直接执行下一步骤。

　　6)判断是否满足寻优条件，若满足则结束寻优过程，否则回转执行步骤2)。

　　7)获得优化好的核函数参数g和惩罚因子G。

　　4 案例分析

　　为了验证基于改进粒子群算法优化的电力负荷预测方法的性能，本文选择某地居民小区为基本单位进行用电信息采集，对用电情况进行验证分析。

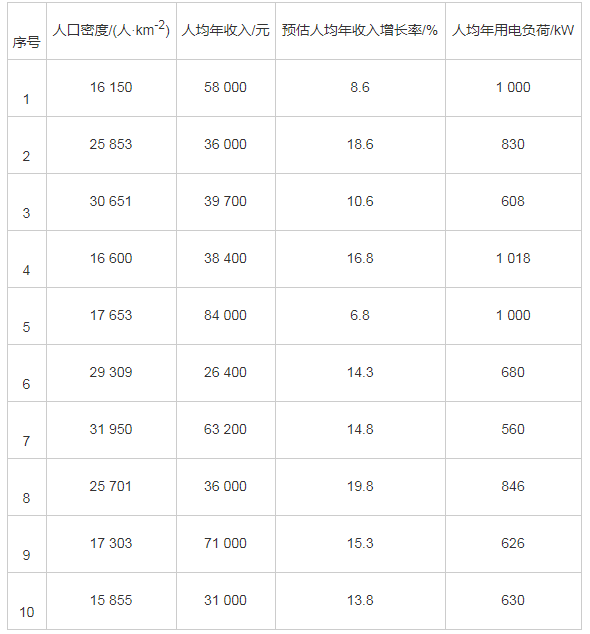
　　在数据采集过程中，应该充分考虑各个性能参数：人口密度、人均年收入、预期年收入增长情况及人均年用电预测负荷等。本文收集10个小区的样本数据以及每个小区近3年的用电信息作为负荷预测的输入样本，样本数据如表1所示，代入基于改进PSO-SVM负荷预测模型，并获得输出数值。

　　表1 用电样本信息

　　本文通过均方根误差eRMSE和平均绝对百分比误差eMAPE两个参数作为电力负荷预测的评价指标。

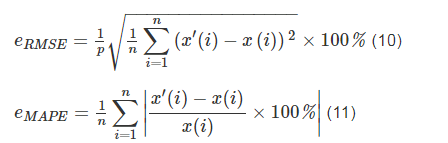
　　通过SVM模型与PSO-SVM模型进行比较，选用eRMSE和eMAPE两个参数作为电力负荷预测的评价指标，代入表1数据，经分析得出表2所示的误差指标。

　　表2 电力预测误差指标 

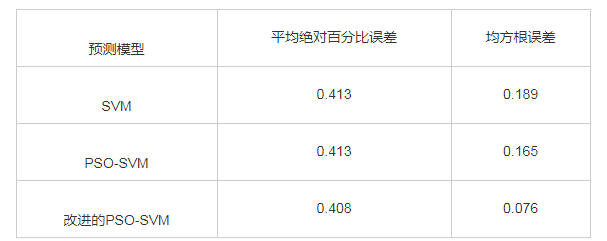
　　根据电力预测误差指标对比分析，改进的预测PSO-SVM模型的均方根误差及绝对百分比误差相对较小，准确率明显高于SVM和未改进的PSO-SVM模型。

　　5 结语

　　本文通过深入剖析支持向量机及粒子群算法的基本原理及应用的优缺点，提出了通过引入粒子距高斯变异对PSO-SVM算法进行改进。改进后的算法不仅提升了模型的预测精度，而且还有着快速收敛的特点，对后期深入研究电力负荷预测具有重要的参考意义。

　　参考文献

　　[1]苏振宇，龙勇,赵丽艳基于regARIMA模型的月度负荷测试效果研究[J].中国电力, 2018,51(5):167-171.

　　[2]吴潇雨，和敬涵, 张沛,等.基于灰色投影改进随机森林算法的电力系统短期符合预测[J].电力系统自动化, 2015(12):50-55.

　　[3]唐玮，钟士元，舒娇，等.基于GRA-LSSVM的配电网空间负荷预测方法研究[J].电力系统保护与控制, 2018.46(24):82-88.

　　[4]唐宏,冯平,陈镜伯，等 萤火虫算法优化SVR参数在短期电力负荷预测中的应用[J].西华大学学报(自然科学版),2017,36(1):35-38.

　　[5]范海虹基于萤火虫算法的短期电力负荷预测方法研究[J].中国电力，2021,54(3):141-148.

　　[6]纪震,廖惠连，吴青华.粒子群算法及应用[M].北京:科学出版社，2009.

　　[7]黄洋,鲁海燕，许海波,等.一种动态调整惯性权重的简化均值粒子群优化算法[J]小型微型计算机系统, 2018,39(12):2590-2595.

　　[8]裴宇航，刘景森,李煜.一-种动态调整惯性权重的自适应蝙蝠算法[J].计算机科学, 2017(6):240-244.

　　[9]赵志刚，黄树运，王伟倩基于随机惯性权重的简化粒子群优化算法[J].计算机应用研究, 2014(2):361-363.

　　[10]刘振,周先存.基于独立权重和分级变异策略的粒子群算法[J].吉林大学学报(理学版),2017(2):333-339.