2 研究方法。
2. 1 联合分布及边缘分布模拟。
雨潮遭遇属于两变量联合分布问题。设降雨系列 X 和潮位系列 Y 为连续的随机变量,F ( x) 和 F ( y) 分别为 X 和 Y 的累积分布函数。根据 Sklar 定理,雨潮遭遇联合分布 F ( x,y) 可定义为:
F( x,y) = C[F( x) ,F( y) ]= C( u,v) ( 1)。
式中: C ( u,v) 为边缘分布为[0,1]区间的 Copula 联结函数,u=F ( x) ,v=F ( y) .
Copula 函数类型众多,其中仅含一个参数的 Archimedean Copulas 计算简便,已广泛应用于水文两变量联合分布模拟[14].本文采用 Clayton、Frank、Gumbel-Hougaard( GH) 和 Ali-Mikhail-Haq( AMH) 共 4 种 Archime-dean Copulas 作为雨潮遭遇联合分布备选模型。雨潮遭遇之间的相依性度量采用 Spearman 秩相关系数 ρ 、Kendall τ 和 Pearson 古典相关系数 γ ,边缘分布模拟考虑了 5 种水文领域应用较为广泛的三参数分布模型,即广义极值( Generalized Extreme Value,GEV) 、广义帕累托( Generalized Pareto,GP) 、广义 Logistic( General-ized Logistic,GLO) 、皮尔逊Ⅲ型( Pearson III,PE3) 和广义正态( Generalized Normal,GNO) .Copula 模型参数采用 Kendall τ 估计,边缘分布模型参数则采用较稳健的线性矩法估计。
雨潮遭遇边缘分布模型拟合采用 K-S 方法的检验统计量 D[15],联合分布 Copula 函数拟合采用基于Rosenblatt 变换的 Cramervon Mises 检验统计量之一 S( B) [16-18].若有多个模型通过了统计检验,则根据均方根误差( Root-Mean-Square Error,RMSE) 和赤池信息准则( Akaike Information Criterion,AIC) 进一步优选[18].
2. 2 联合重现期。
多变量联合分布概率,理论上有多种组合。就雨潮遭遇设计而言,通常关注两者均大于特定值的超阈分布概率。因此,若雨量系列 X 和潮位系列 Y 的超阈分布概率分别为 F-( x) 和 F-( y) ,有:
F-( x) = u-= P( X > x) = 1 - u ( 2)。
F-( y) = v-= P( Y > y) = 1 - v ( 3)。
则雨潮遭遇超阈联合分布概率 C^(u-,v- ) 为:
C^( u-,v-) = P ( X > x ∩ Y > y) = 1 - ( u + v) + C( u,v) ( 4)。
联合重现期计算时,由于存在两变量多种组合 ( u,v) ,使得超阈联合分布概率 C^u-,v-( ) 或联合重现期相同。有关研究表明[12],较大重现期对应的危险事件可能会被较小重现期识别为安全事件。为此,多变量联合分布研究在传统联合重现期基础上提出了二次重现期概念,即以联合概率相等的一系列事件为临界曲线,来识别危险事件和安全事件[19].二次重现期对应的超阈联合分布概率,可以用基于 C^u-,v-( ) 的 Kendall 分布函数 K^C来表示,即:
KC^( q) = P( C^≤ q) ( 5)。
式中: q∈( 0,1) .由于 KC^ 无法通过解析式求解, 其 理论值采用 Monte Carlo 法模拟, 通过极大似然法估算,即:
式中: n 为 Monte Carlo 随机模拟( u,v) 组合数,拟取
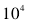
。
因此,雨潮遭遇超阈的单变量重现期 TX和 TY,传统联合重现期 TXY和二次重现期 TK分别为:
式中: NE为基于 POT 方法的暴雨事件年均发生次数,对于采用 AM 方法的雨潮系列,NE为 1.

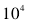 。
。