掺气水流流场测量中光流法的使用进展及前沿问题,水文学论文

　　摘要：　水利设施中掺气水流运动速度估计一直是水气两相流领域重点研究的课题，由于掺气水流中气泡复杂的演变机制和剧烈的湍动瞬变，导致现有的测量技术难以准确的表征水流流场情况。基于光流法的流场可视化技术因其独特的优势而成为图像识别领域重点研究的方向。光流法能够根据像素亮度计算出细观气泡运动的高分辨率光流场，弥补了传统的基于粒子图像测速技术的不足。为了全面的反映国内外研究人员应用光流技术对掺气水流流场可视化估计的进展，本文从经典光流法的原理出发，综述了目前用于掺气水流中的几种光流技术及其特点，然后总结了光流技术在处理掺气水流这种复杂场景时采用的关键技术和参数选择情况。最后，探讨了光流技术在掺气水流应用中所面临的挑战和前沿问题，并对其未来的发展做出展望。

　　关键词 : 掺气水流;光流法;流场可视化;进展;关键参数;前沿问题;

　　Abstract：　Velocity measurement in highly aerated flow is an important research topic in both fields of air-water two-phase flow and hydraulic engineering. Due to the complex evolution mechanism and rapidly turbulent fluctuations of self-aerated or artificially-aerated bubbly flow, the current measurement techniques have their limitation in accurate characterization of the flow velocity and velocity turbulence. The flow visualization technique based upon the optical flow has become a significant research interest in the field of image recognition due to its unique advantages. According to the brightness of pixels on the image, the optical flow method enables calculation of the high-resolution optical fields for the meso-scale movement of bubbles, making up for the shortcomings of traditional particle image velocimetry. Aiming to provide a comprehensive picture of the progress and the state of the art in the application of optical flow technique in the aerated flow field visualization, this paper firstly introduces the principle of classical optical flow method, reviewing the several applicable optical flow techniques in highly aerated flow at present. Then, the key processing techniques and parameter selections for the application of optical flow method to the complex cases of highly aerated flow are summarized. Finally, the challenge and frontier scientific and practical issues faced by the optical flow techniques in highly aerated flow are discussed, and the potential future development directions are prospected.

　　Keyword：　highly aerated flow; optical flow method; flow visualization; review; key parameters; frontier issues;

掺气水流流场测量中光流法的使用进展及前沿问题

　　0、引言

　　近40年以来，我国的水利水电工程建设事业蓬勃发展，并达到世界领先水平。这些大型水利工程大多建在狭窄的河谷里，具有水头高、泄量大的显着特点[1,2]，其中涉及的核心问题之一是高速水流泄洪时的水体巨量掺气问题[3]。掺入的气泡在增加消能效率的同时，容易产生泄洪水流雾化[4]和水体中总溶解气体过饱和[5,6] 现象。尽管目前关于高速水流掺气机制的研究已经取得了一些基础成果，但掺气水流伴随着剧烈的湍流作用和复杂的三维运动，现有的研究成果仍不足以让我们深刻理解高速水流的掺气机理和动力学特征，这也成为高速水力学水气两相流学科发展面临的重大挑战之一[7,8]。

　　目前国内外对大型水利工程高速水流掺气问题的研究主要依赖于模型实验。尽管对单相流研究已经取得了丰富的成果，然而对于水气两相流来说，即便是最基本的流动特性的测量也并非易事[8]。传统的侵入式的仪器，如毕托管、声学多普勒流速仪（ADV）和激光多普勒流速仪（LDA），由于大量气泡的不利影响而不能用于高含气水流中[9]。当前研究人员广泛使用的测量设备为侵入式的电阻式探针和光纤探针[10]，借助于信号后处理技术，能够实现掺气水流气泡特性的表征，包括水气界面速度和湍流特性[11,12,13]。然而这种测量方法的局限性在于只针对水流流过针尖的极一小块区域进行测量，难以反映掺气水流内部二维乃至三维的流场特征。而且水体中的气泡处在不断的分裂、合并、聚集和破灭，侵入到水体中的探针必然在一定程度上影响气泡的存在形式和气泡的动力学过程，进而影响流场的测量。

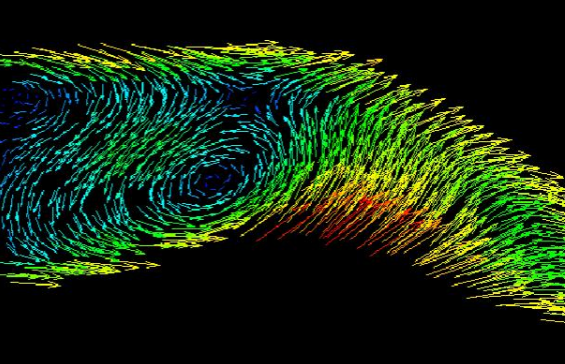
　　除了上述侵入式探针，基于图像识别技术来确定水流流场的方法在近年也来有所发展，虽然无法达到侵入式探针的测量精度，但流场成像可以一次呈现全流场速度分布，具有广阔的应用前景。目前传统的非侵入性的基于图像识别方法主要为粒子成像测速技术（PIV）[14,15]、气泡图像流速仪（BIV）[16,17]和粒子跟踪流速仪（PTV）[18]。然而PIV局限于清水或气泡很少的情况，BIV和PTV虽能够提供气泡速度场分布，但由于气泡对光线的反射容易影响示踪粒子的跟踪[19,20]。最近的研究显示，计算机视觉领域的光流法[21]，通过计算每个像素点的亮度模式的变化即可得到全流场的速度信息，在水气两相流成像上的应用能够提供与BIV相当的甚至高于BIV的观测精度[19,21]。光流法的最大的优点是其刻画高分辨率速度场的能力，即通过每个像素点亮度的变化即可得到稠密的速度矢量场，从而进一步分析强掺气水流的湍流特性，目前已成功应用于各领域含气水流中，如水跃[22,23]、溢洪道[24,25,26]、涌潮[27,28]、射流[29]、溃坝[19,30]和自然河流[31]等。

　　因此，本综述旨在概述光流法在水利工程掺气水流流场可视化中的最新研究进展，及其面临的前沿问题。第一部分简要介绍经典的光流算法原理；第二部分综述光流法用于掺气水流流场可视化的最新进展；第三部分阐述光流法面临的挑战及尚待研究的问题。

　　1、光流法原理

　　光流是一种二维的瞬时速度矢量场，是通过摄像机拍摄三维运动物体在二维平面图像上的投影来表征的，表现为图像平面亮度模式的表观运动，物体的运动情况通过平面上每个像素点运动矢量的集合确定，如图1所示的三维物体与二维平面投影之间的关系。光流最早是在1950年Gibson为描述图像模式运动的速度提出的[32]。真正有效的光流技术当属1981年Horn和Schunck（HS方法）[33]以及Lucas和Kanada（LK方法）[34]在计算机视觉领域所提出的计算方法，分别属于全局求解光流场和局部邻域求解光流场。这两种方法使用的前提都是基于两帧之间图像像素的亮度保持不变的假设，被称为亮度一致性假设。后来进行图像全局求解的HS方法成为了以后主要的计算光流场的经典方法[35,36,37]，并由此衍生出诸多先进的算法。因此在这里将简要的引入经典的HS光流算法加以介绍。

　　根据运动物体像素点的亮度在瞬时运动过程中应保持恒定，可得到以下数学表达式

　　I(x,y,t)=I(x+uΔt,y+vΔt,t+Δt)（1）

　　式中：u为运动目标沿x方向的光流矢量，Δx=uΔt；v为运动目标沿y方向的光流矢量，Δy=vΔt；x和y分别为图像上的一个像素在水平方向和竖直方向的位置；I(x, y, t)为当前图像帧在像素位置(x, y)处的灰度值；I(x+Δx, y+Δy, t+Δt)为该像素在下一帧图像上新位置(x+Δx, y+Δy)处的灰度值；

　　HS方法采用一阶泰勒展开来线性化（1）式等号的右边项[33]，同时根据灰度值不变性假设，当Δt→0时，可近似得以下表达式

　　u?I?x+v?I?y+?I?t=0（2）

　　上式就是着名的光流计算基本等式，也称为光流约束方程。可写成以下的矢量形式

　　?I?w+It=0（3）

　　由于光流矢量w = (u, v)有两个分量，因此利用式（3）求解光流场是一个数学上的欠定问题，需要补充另外的约束方程才能求解。

　　图1 三维运动物体与二维平面投影之间的关系简图

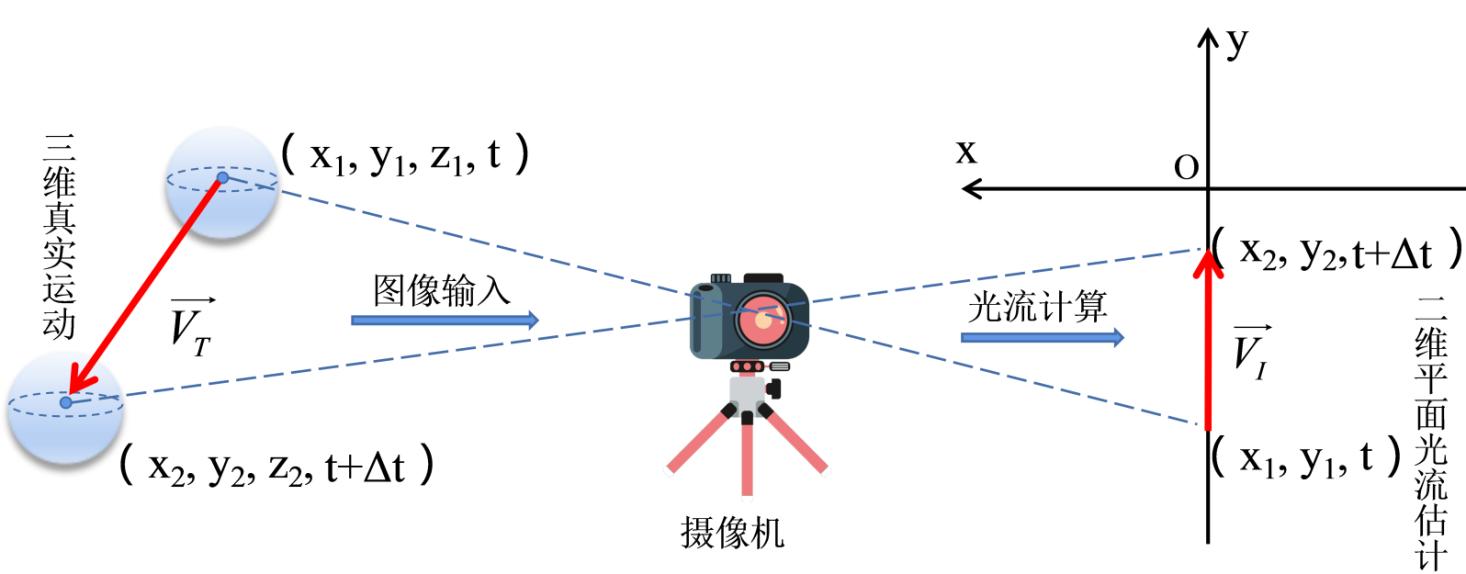
　　Fig. 1 Sketch of the relationship between 3D moving object and 2D plane projection

　　HS方法认为基于亮度一致性原理可能导致光流场被低估，因此引入光流的整体平滑性假设来求解光矢量，即在一个固定点（x, y）与它的一个邻域?2u+?2v内的光流变化应尽可能的趋向于0，这是求条件极值时的约束条件，在数学上表达为

　　|?u|2+|?v|2=min{(?u?x)2+(?u?y)2+(?v?x)2+(?v?y)2}（4）

　　综合式（3）和式（4），引入一个全局能量约束函数，光流u和光流v的计算可变为如下的变分问题

　　E(u,v)=?(Ixu+Iyv+It)dxdy数据项+?α2(|?u|2+|?v|2)dxdy平滑项（5）

　　式中：α是一个平衡常数，用于平衡前后两项以满足能量函数约束条件。一个越大的α值对应一个越平滑的运动向量。通过最小化（5）式的能量约束条件即可求解任一像素点的光流矢量，可采用迭代的方式实现。上述HS方法容易实现，可求解稠密的瞬时光流速度，但是存在以下不足：1）HS方法引入了整体平滑性约束条件，会导致物体形状纹理信息的缺失；2）基于亮度一致性原理，光照亮度的变化和运动的模糊导致该假设不易成立；3）只适用于运动位移较小的运动情况[38]；4）不同的视频图像可能有不同的质量，一个固定的平衡常数可能是不合适的[39]。

　　2 、光流法在掺气水流流场测量中的应用进展

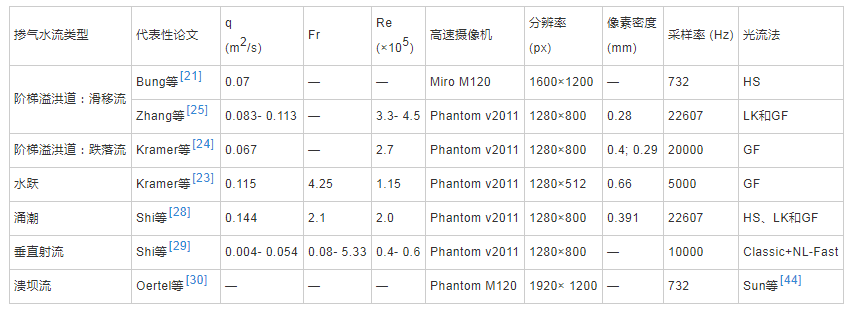
　　自从1981年Horn和Schunck提出经典的光流思想来确定运动目标的信息以来，40年来基于这一思想提出了许多改进的方法和衍生出先进的光流计算方法，并被广泛的应用到工业生产实际中的诸多不同领域，如机器人视觉[40]，视频图像压缩、冲突预测、图像分割，流体力学运动估计[41]等。光流法最初在水利工程水气两相流中的运用起源于2016年Bung的研究。Bung等[21]使用经典的Horn-Schunck方法结合图像滤波技术成功的测量了阶梯溢洪道上掺气水流的光流速度场，并在后续的研究中表明光流法相对于其他图像测速方法（即PIV和BIV）具有相当的精确度[42,43]，而且最大的特点是光流法在每个像素点能提供稠密的高分辨率速度场，表明了光流法在水气两相流运用中的巨大优势。随后，研究人员使用光流法开展了其他掺气水流的测量，如水跃[23]、涌潮[19,28]、射流[29]、溃坝流[30]等，光流法一时成为水利工程水气两相流领域热门的研究方向之一。表1总结了光流法在各类型掺气水流应用中的具有代表性的研究。表中：q为来流的单宽流量；Fr为来流弗劳德数，Fr = V/(gd)0.5；Re为来流雷诺数，Re = ρVd/μ，V和d分别为来流速度和水深，g为重力加速度，ρ为水的密度，μ为水的动力粘度；像素密度代表图像上每个像素代表的实际距离。

　　表1 光流法在各类型掺气水流应用中的代表性研究

　　2.1、常用的光流法

　　没有任何一种光流法适用于不同场景拍摄出来的图像序列，而应该为每种图像序列选择适合的光流技术[45]。在水气两相流领域，自Bung首次使用经典的HS光流技术确定阶梯溢洪道掺气水流的光流速度场以来，研究人员开始尝试使用多种光流技术运用到不同类型的水利设施的掺气水流中，并深入对比与分析了各种光流技术的优势与不足。

　　不同于HS方法对图像上的所有像素进行全局处理，一些局部的方法，例如LK方法[34]和Gunnar-Farneback（GF方法）[46]，不对图像的每个像素处理，而是选择像素固定点周围的邻域进行光流计算，因此相对于HS方法来说对噪声具有更为鲁棒的性能。LK方法选取像素点周围的一个邻域，并假设光流在这个邻域是一个常数，然后使用加权最小二乘法对邻域中的所有像素求解光流方程（即公式（2））。这种假设的前提是目标物体前后两帧之间的位移很小，并且在像素点的邻域内具有运动一致性[34]。GF方法是Farneback在2003年提出的一种基于梯度的方法，假设图像梯度恒定且局部光流恒定，利用多项式对每个像素的邻域信息进行近似表示，可计算出图像上所有像素的光流[46]，因此GF方法具有对噪声鲁棒和计算稠密光流两大优势，并且具有更高的计算精度和计算效率，被广泛的应用于水气两相流的光流场计算中[19,22,23,27,28,47]。如图2所示的Kramer等[23]采用GF方法对水跃水气界面速度的流场可视化表示，χ表示距离水跃发生点的水平距离。

　　图 2 GF光流法对水跃中的运动速度场估计（来源：Kramer等[23]）
图 2 GF光流法对水跃中的运动速度场估计（来源：Kramer等[23]）

　　Fig.2 Estimation of velocity field in hydraulic jump by GF optical flow method (Taken from Kramer et al. [23])

　　同样地，由于考虑到HS方法对于噪声的敏感性，Sun等[44,45]基于经典的HS方法在理论上提出了数种先进的光流法，并且比较和研究了这些光流技术处理的优势。Oertel等[30]运用Sun提到的9种光流技术计算了二维溃坝流中的速度场，并与PIV测速和手动粒子跟踪测速结果对比，定量地证明了光流法具有更小的误差，能提供高密度的速度信息，与其他的几种光流法相比，OF8（Classic+NL-Full）方法显示出了更加平滑的速度分布和更高的准确度。Shi等[29]也运用Sun提出的一种先进的光流法“Classic+NL-Fast”，计算了垂直射流的二维光流速度场。这种技术是在经典的HS方法中附加一个鲁棒的中值滤波前处理技术来实现的，然而却增加了计算成本。表2简短的总结了目前在掺气水流中常用的光流法及其特点。

　　表2 水气两相流领域常用光流法总结

　　Zhang等[25]尝试在阶梯式溢洪道高速掺气水流中运用两种局部方法研究，结果表明拉格朗日式的LK方法更适合用来表征气泡运动的路径，而欧拉式的GF方法来更适合用来计算速度流场。同时设计验证试验与电阻式探针测量结果相对比，验证了光流法的可靠性，并通过GF方法计算了阶梯溢洪道水流的湍流强度、涡量和湍动能。采用同样的参数设置，Zhang等[26]运用GF方法获得了阶梯溢洪道上部分阶梯空腔填充实验模型上滑移流的流场分布，并与无填充的阶梯对比，分析了两个模型的平面应变率和涡量，湍流强度和湍动能场，以及湍流特征长度和时间尺度的差异，突出了阶梯掺气水流的强湍流性和流动复杂性。

　　对行进中的涌潮研究，Shi等[28]同时运用HS、LK和GF三种方法计算了水气两相界面的瞬时光流速度场。结果表明三种光流技术的结果基本是一致的，但是在水槽的底板附近清水区域中由于光照亮度的变化导致HS方法出现了一些无意义的结果，同时旋滚区域的流场表现出不连续性，论证了HS方法对于噪声非常敏感。最后运用直接数值模拟（DNS）和角误差计算定量证明了最适用于水气两相流的光流方法是GF方法。随后，Shi等[47]利用上述GF方法的参数同时计算了三种不同的水气混合流，包括静态水跃、稳定垂直射流和行进破碎涌潮，表明了光流法的在水气两相流速度表征中的能力。除此之外，对涌潮自由表面采取俯视拍摄的方式，Wüthrich等[27]运用GF方法计算了涌潮自由表面水气混合流的可视化光流速度场，表明了沿水槽纵向方向的速度幅值向远离旋滚发生点的方向逐渐减小，随后分析了自由表面的湍流波动特性。

　　2.2、光流法的关键问题及参数评估

　　相比于光流法在其他领域的应用，光流法在掺气水流场景的应用要复杂的多。首先，水利设施中的掺气水流处在高速运动中，这种大位移的运动限制了光流法的开展。其次，在进行图像拍摄时，亮度不均匀、气泡对光照的反射、拍摄景深后水流背景的移动、壁面附着液滴等问题都会引入许多的噪声，造成光流技术计算精度下降。此外，在光流计算时一些关键的采样参数和图像后处理技术也对结果造成很大的影响，例如采样率和采样时间、图像像素的亮度值、金字塔层数、光流法局部邻域大小和滤波技术等。本节对光流法在掺气水流应用中面临的关键问题、对应的改进技术以及特殊地采样和处理参数进行综述。

　　2.2.1、图像噪声问题

　　噪声通常是由于摄像机结构、设备温度变化、光源强度变化等因素进入到图像中的，并且随着光流的计算累积而增强。Fermuller等[48]指出了图像噪声导致光流幅值和方向的低估。对输入图像采取滤波处理是移除噪声和增强图像结构的方法。目前主要采用的滤波方法有高斯滤波[33]、中值滤波[45,49,50]、双边滤波[51]和卡尔曼滤波[52,53]。Song等[54]提出了一种两步去噪的方法，第一步采用高斯滤波来移除高频噪声，第二步用正则化方法进行去模糊处理。Buades等[55]采用非局部的滤波方法去噪；Liu等[56]设计了一个自适应的去噪算法，并整合到光流计算中来移除相机引入的偶然噪声和自身噪声。

　　Barron等[36]研究表明HS方法相较于其他局部的方法来说，HS方法对于图像的噪声更加敏感，然而HS方法是许多先进的光流技术的基础，它作为一种全局的方法能够求解图像平面每个像素的光流场，从而提供稠密的光流速度矢量，便于进行后续参数的分析，因此研究人员对此也进行了改进。公式（5）中α的选择非常重要，因为噪声的存在会增加数据项相对于平滑项的权重，从而大大地减小平滑的程度[57]，通常来说α的取值为1，而Shi等[28]敏感性分析表明α取值为2是最合适的。为了提高平滑项在消除异常离群数据、保持边界不连续性、低纹理区传播信息的能力，研究人员针对平滑项提出了非局部正则化[45,58,59]、时空正则化[60,61]与基于图像流[62,63]的改进方法。

　　2.2.2 、图像亮度的变化问题

　　针对不满足亮度一致性假设问题，提出了鲁棒的常数约束[38,63]、纹理结构分解[64]和颜色空间[60,65]三种方法。Parenberg等[38]发现了其他高阶的常数约束也是非常有用的，具有很强的鲁棒性，例如Hessian和Laplacian常数约束；Mohamed等[66]针对数据项提出了一种鲁棒的基于局部纹理特征的亮度常数约束；Wedel等[67]将输入图像分解为结构和纹理分量，并以纹理分量为重点，将两者线性组合重建新图像；Golland等基于运动下的颜色光度不变性，设置了HIS颜色空间和RGB亮度函数两种颜色方案来分析和比较运动的光度不变性；Weijer等[68]研究了光度不变的不稳定性，提出了一个新的基于光度变化的光流方法来解决由于相机的移动和光源变化造成的图像阴影移动、阴影变化和镜面反射问题。

　　2.2.3、采样参数

　　Liu等[69]指出光流的误差主要取决于连续两帧之间的时间间隔以及图像的亮度梯度。在一定的时间间隔下，更大的亮度梯度对应更小的光流计算误差。而且，光流法的准确性依赖于图像亮度的分布，与电阻式探针数据的误差分析比较表明了原始图像的像素亮度值大约为100-150可能实现更准确的结果，而更小的亮度值对应于更大的误差[21]。图像的采样帧率，即连续两帧之间的时间间隔同样影响光流计算的准确性。Zhang等[25]和Kramer等[24]的敏感性分析表明，如果要实现湍流特性的表征，至少5000Hz的采样频率是必须的，而采样的时间应控制在10秒以上才能得到更精确的水气两相流时间平均特性。然而，高的采样频率和时间对应大量的数据存储和高的计算成本，在实验时应充分评估好两者的关系。

　　2.2.4 、运动大位移问题

　　光流法应用的前提是限制在小位移目标物体运动假设，对于大位移的运动可能会产生较大的误差估计，采用一种多分辨率的图像金字塔技术可能很好的解决大位移运动问题。图像金字塔技术是对单一的图像使用同一种滤波技术而不是对一副图像使用多种滤波技术[70]。图像金字塔的原理是使用一个比例因子对原始采样图像缩放，形成模糊化的较低分辨率图像，然后对生成的图像再次运用同一个比例因子继续缩放，重复数次之后得到了分辨率越来越低的一组图像，以原始图像为底层依次向上排列即可构成图像金字塔。事实上，这个金字塔就是图像的空间频域。可以看出金字塔最上层图像分辨率最小，代表的位移最大。光流法计算时从金字塔最顶层开始向下一层求解，每一层得到的矢量值作为下一层求解的初始值，经过逐层依次向下求解和结果修正，实现了位移“由粗到细”的计算[45]，如图3所示金字塔技术对图像进行多分辨率操作过程。Anandan等[71]在1987年首先在变分模型中引入单向粗细化格式来计算稠密速度流场，之后图像金字塔思想被广泛的运用到大位移计算中。Bruhn等[72]和Zimmer等[60]针对图像金字塔提出了一种先进的从粗到细的变形技术：双向多重网格方案。

　　图3 多分辨率图像金字塔示意图（来源：Shi等[28]）

　　Fig .3 Sketch of multi-resolution image pyramid (Taken from Shi et al.[28])

　　2.2.5 、图像金字塔层数选择

　　Bung等[21]运用HS方法计算阶梯溢洪道掺气水流时，对金字塔层数的敏感性分析表明5层金字塔可得到一个较为准确的结果，而较多或者较少的层数则会产生更大的误差和速度不连续。当采用GF方法计算时，Bung等[73]得到了相似的结果。然而Kramer等[24]敏感性分析表明金字塔的层数几乎不影响光流速度场的分布。这种矛盾可能是由于Kramer拍摄的运动位移小于Bung一个数量级导致的，毕竟Kramer使用的采样频率至少为5000Hz，而Bung的采样率仅为732Hz。在后续的水气两相流研究中由于使用较高的采样率，2层的金字塔被普遍的接受[19,23,28,47]。除此之外，最上层金字塔的图像分辨率也有一定的规定，一个合理的原始采样图像的分辨率应该与金字塔最顶层的图像分辨率相耦合。Bung等[21]计算表明金字塔最顶层的图像分辨应为25像素左右，这与文献[45]推荐的20-30的最优像素值大致是一致的。

　　2.2.6、滤波技术和局部邻域选择

　　为了移除气泡和液滴对光的反射带来的不均匀光照，Kramer等[24]把ad-hoc滤波技术施加到光流计算的前处理中，来滤除图像低信噪比信息和边缘区域。均值滤波、高斯滤波和中值滤波也被广泛的用来过滤图像噪声和离群值。Sun等[44]建议中值滤波的滤波尺寸是5×5像素，而Bung等[21,43]在含气水流研究中表明中值滤波的尺寸大约是15×15像素。Kramer等[24]分析了均值滤波的尺寸为10-15像素，Wüthrich等[27]高斯滤波的窗口大小为15像素。一个更小的滤波尺寸和更大的邻域尺寸会造成光流速度场更大的波动[23]。对于GF光流法局部邻域尺寸的选择，Kramer等[24]敏感性分析表明1-5像素的局部邻域大小是合适的，Zhang等[25,26]采用的邻域大小为7像素，Shi等[28] 角误差计算表明选择5像素产生最小的误差，而LK方法的局部邻域大小取20-25像素才是最合适的。

　　2.3 、光流法与其他图像处理方法比较

　　目前在流体速度的测量中使用的图像处理方法通常为PIV、BIV、PTV和光流法。PIV方法通过跟踪水流中撒播的粒子而获得流场，然而在掺气水流中由于气泡对粒子的遮挡而容易遗失对粒子的跟踪，因此PIV只适用于测量清水或气泡非常少的流场。PTV是一种拉格朗日的方法，使用固体示踪粒子来进行追踪可得到粒子的运动轨迹和速度。然而由于气泡对光线的反射，容易把具有规则形状的气泡当成粒子而跟踪，影响测量准确性。BIV是在PIV的基础上发展起来的技术，它结合了图像阴影技术以及PIV中连续两帧间相关性测速技术，将气泡图像与图像中水气两相界面产生的“纹理”相关联，不必像PIV技术一样必须撒播示踪粒子而可直接使用气泡作为跟踪粒子，因此可用于测量掺气水流的速度场。

　　目前光流法与BIV对比研究表明，两者对于刻画掺气水流速度场的结果几乎是一致的，但综合来看光流法对掺气区域的表征更为鲁棒[21,42]。具有高分辨率的图像能更好地表征结果的质量。光流法最大的优势是表征全局稠密速度场的能力，可获得图像上每个像素点的速度信息，从而便于下一步开展对内部湍流波动的研究。而通过BIV技术获得了较低图像分辨率，容易造成数据的不连续，并且询问窗口大小的选择可能会导致位移向量偏向整数像素值，称为“像素锁定”[74]。另外计算过程执行奈奎斯特采样定理而总是会产生过低的位移估计。光流法是一种微分的方法，而BIV是一种积分和统计的方法，相比于光流法，BIV计算效率较高。

　　3、光流法在掺气水流流场测量中的前沿问题

　　由于掺气水流流场估计场景的复杂性，以下关于光流法的问题需要进一步研究：

　　（1）亮度一致性问题。光流法作为一种微分的方法，应用光流法首先要考虑的问题是图像序列亮度问题，均匀的光照强度是应用光流法的前提。然而由于当前使用的场景是水利设施中的掺气水流，一方面光照受到水和空气的反射造成局部的光照不均匀，另一方面容易产生玻璃壁面上水流的附着和脱落而造成光线反射。其次，气泡在输运过程中由于气泡动力学原因总是伴随着气泡的聚集、合并、变形和破碎，造成连续图像序列目标物体和光照强度的变化。最后，掺气水流中掺气浓度和气泡频率的分布也会影响计算结果，Zhang等[25]指出当掺气浓度大于50%时，光流误差导致的计算结果不再令人信服，远低于电阻式探针的测量结果，这同样可能是由于上表面流动区域飞溅的液滴或喷雾产生的玻璃壁面附着和不均匀的光照引起的，然而这点在以前的研究中却并没有被明确。

　　（2）边壁效应问题。光流法的运用得益于高速摄像机穿过透明的边壁拍摄的掺气水流图像序列，然而由于边壁摩擦阻力的存在，阻碍了边壁附近掺气水流湍流相干结构的形成和发展，产生了不同于中心流动区域的流态，导致边壁附近的掺气浓度、气泡频率和速度分布与中心线相比相差10-40%[24,25]。因此，基于边壁记录的光流速度场能否代表内部水气两相流的流态仍然需要进一步的研究，这也是其他基于边壁测量的技术，如PIV、BIV和PTV，同样需要回答的问题。

　　（3）拍摄硬件问题。获得的光流场数据的质量是直接与拍摄时的高速摄像机、镜头和光源等硬件设施的性能密切相关的。具有高分辨率和高采样频率的超高速摄像机产生更好的输出图像和更为准确的光流结果。其次，镜头的选择是关键的，一是具有快速定焦功能，这样可以使用更短的曝光时间获得更清晰的目标；二是最小化图像失真，这样能缩短光流计算时迭代的时间。最后，光源的效果同样影响光流数据的好坏，不同类型的掺气水流对应于不同的光源配置，在正式实验前进行光源的配置试验来达到最优的灯光效果是非常必要的，甚至根据需要配备超强亮度的LED光源阵列。

　　（4）计算效率问题。光流法采用复杂的变分方式进行计算，计算效率低下，而随着迭代次数的增加所需时间成倍增加。此外，实现高含气水流流场估计需要高采样频率的视频序列，大量的图像在处理时无疑进一步降低了光流法的计算效率，无法实现运动的实时评估。最近发展起来的基于卷积神经网络（CNN）的光流估计技术虽然能够实现更高的计算速度和计算精度[75]，但是需要大量的样本来训练模型，且技术上还不够成熟。因此提高掺气水流流场估计光流算法的计算效率，在未来仍然值得大量研究。

　　（5）表征湍流特性问题。应用光流技术获得了瞬时的光流速度数据，从而可以考虑湍流特性的计算，如湍流强度、湍流积分长度和时间尺度等。到目前为止，尽管湍流特性计算已经取得了一些成果，然而由于光流法本身存在的一些缺陷，可能不能准确的表征湍流结构。例如LK方法假设局部邻域内的光流矢量保持恒定，在这种情况下湍流长度尺度小于邻域尺寸的湍流结构可能会被忽略。GF方法能够遍历每个像素点来获得湍流特性，看似是比较合理的方法，可是却完全依赖于平移后的二次多项式。而HS方法由于对噪声很敏感以至于不能应用到水气两相流光流速度场的计算中。因此，光流技术对湍流特性的表征在未来是值得进一步研究的方向之一。

　　4、结语

　　基于光流法的目标物体运动估计技术一直是计算机视觉领域研究的热点与难点。对于水利工程中的高速掺气水流来说，对流场的精确测量是一项复杂的工程。而气泡与水流相互作用的复杂气泡动力学特性限制了许多测量技术的开展。相较于传统的测速技术，基于光流法的流场估计技术表现出了其刻画稠密光流场的能力，对于瞬时速度场的估计具有更为鲁棒的性能。本文综述了目前用于掺气水流中的几种光流法及其特点，以及在处理这种复杂场景时需要详细分析的采样参数和图像处理技术，并从光流技术、拍摄方式、后处理技术和结果分析等方面系统总结了光流法应用于掺气水流中所面临的问题。光流技术的使用有助于进一步认识高速掺气水流的流场分布和相关的气泡动力学过程等基础科学问题，为水利泄洪消能工程和水环境保护提供指导。

　　参考文献

　　[1]谢省宗,吴-红,陈文学.我国高坝泄洪消能新技术的研究和创新[J].水利学报，2016, 47(3): 324-336.
　　[2]许唯临.高坝水力学的理论与实践[J].人民长江, 2020, 51(1): 166-173+186.
　　[3]张建民高坝泄洪消能技术研究进展和展望[J].水力发电学报, 2021, 1-20.
　　[4]练继建,何军龄,缑文娟,等.泄洪雾化危害的治理方案研究[J].水力发电学报, 2019, 38(11): 9-19.
　　[5]张亦然杜秋成,王远铭,等总溶解气体过饱和含沙水体对齐口裂腹鱼影响的实验研究[J].水利学报, 2014, 45(9): 1029-1037.
　　[6]李文红,陈英旭,孙建平.不同溶解氧水平对控制底泥向上要水体释放污染物的影响研究[J].农业环境科学学报, 2003, (2): 170-173.
　　[7] Chanson H, Leng X, Wang H. Challenging hydraulic structures of the twenty-first century - from bubbles, transient turbulence to fish passage[J]. J Hydraul Res, 2021, 59(1): 21-35.
　　[8] Chanson H. Hydraulics of aerated flows: qui pro quo?[J]. J Hydraul Res, 2013, 51(3): 223-243.
　　[9] Wang H. Turbulence and Air Entrainment in Hydraulic Jumps[D]. The University of Queensland, 2014.
　　[10] Felder S, Pfister M. Comparative analyses of phase detective intrusive probes in high-velocity air-water flows[J]. Int J Multiphas Flow, 2017, 90: 88-101.
　　[1] Wang H, Chanson H. Experimental Study of Turbulent Fluctuations in Hydraulic Jumps[J]. J Hydraul Eng, 2015, 141(7): 040150-040110.
　　[12] Shi R, Wang H, Chanson H. Bubble convection and bubbly flow turbulent time and length scales in two-dimensional plunging jets[J]. Exp Therm Fluid Sci, 2018, 98: 278-289.
　　[13] Felder s, Chanson H. Phase-detection probe measurements in high-velocity free-surface flows including a discussion of key sampling parameters[J]. Exp Therm Fluid Sci, 2015, 61: 66-78.
　　[14] Lennon J M, Hill D F. Particle Image Velocity Measurements of Undular and Hydraulic Jumps[J]. J Hydraul Eng, 2006, 132(12): 1283-1294.
　　[15] Hornung H G, Willert C, Turner S. The flow field downstream of a hydraulic jump[J]. J Fluid Mech, 1995, 287: 299-316.
　　[16] Rodriguez-Rodriguez J, Marugan-Cruz C, Aliseda A, et al. Dynamics of large turbulent structures in a steady breaker[J]. Exp Therm Fluid Sci, 2011, 35(2): 301-310.
　　[17] Bung D B, Valero D. Image Processing For Bubble Image Velocimetry in Self-Aerated Flows[C]/1 Proceedings of the Proceedings of the 36th IAHR World Congress, The Hague, the Netherlands: Intermational Association for Hydraulic Research, 2015 of Conference: 6594-6601 .
　　[18] Kramer M, Chanson H. Free- Surface Instabiltis in High-Velocity Air-Water Flows down Stepped Chutes[C]// Proceedings of the 6th IAHR International Symposium on Hydraulic Structures 1SHS 2018, Aachen, Germany: Utah State Library, 2018 of Conference: 55-66.
　　[19] Shi R, WUthrich D, Chanson H. Air-water characteristics of a breaking bore roller Part I: Air-water flow properties[R]. Brisbane: The University of Queensland Australia, 2020.
　　[20]邵建斌,胡永亭,陈刚，等.水气两相流中气泡运动的PTV跟踪算法研究[J].水力发电学报, 2010, 29(6): 121-125.
　　[21] Bung D B, Valero D. Optical flow estimation in aerated flows[J]. J Hydraul Res, 2016, 54(5): 575-580.
　　[22] Wang H, Chanson H. Characterisation of transverse turbulent motion in quasi-two-dimensional aerated flow. Application of four-point air-water flow measurements in hydraulic jump[J]. ExpTherm Fluid Sci, 2019, 100: 222-232.
　　[23] Kramer M, Valero D. Turbulence and self-similarity in highly aerated shear flows. The stable hydraulic jump[J]. Int J Multiphas Flow, 2020, 129: 103316.
　　[24] Kramer M, Chanson H. Optical flow estimations in aerated silway flows: Filtering and discussion on sampling parameters[J]. Exp Therm Fluid Sci, 2019, 103: 318-328.
　　[25] Zhang G, Chanson H. Aplication of local optical flow methods to high-velocity free-surface flows: Validation and application to stepped chutes[J]. Exp Therm Fluid Sci, 2018, 90: 186-199.
　　[26] Zhang G, Chanson H. Aplication of optical flow methods to aerated skimming flows above triangular and trapezoidal step cavities[J]. J Hydraul Res, 2019, 57(4): 488-497.
　　[27] Wuthrich D, Shi R, Chanson H. Air-water characteristics of a breaking bore oller. Part 1: Two-phase surface features and strong turbulence[R]. Brisbane: The University of Queensland Australia, 2020.
　　[28] Shi R, Leng X, Chanson H. On optical flow techniques applied to breaking surges[J]. Flow Measurement and Instrumentation, 2020, 72.101710.
　　[29] Shi R, Withrich D, Chanson H. Image-based measurements of air-water flow properties in plunging air-water jet[C]/1 Proceedings of the 8th IAHR International Symposium on Hydraulic Structures ISHS2020, Santiago, Chile: The University of Queensland, 2020 of Conference.
　　[30] Oertel M, Sufke F. Two-dimensional dam-break wave analysis: particle image velocimetry versus optical flow[J]. J Hydraul Res, 2020, 58(2): 326-334.
　　[31] Khalid M, Penard L, Memin E. Optical flow for image-based river velocity estimation[J]. Flow Measurement and Instrumentation, 2019, 65: 110-121.
　　[32] Gibson J J. The perception of the visual world[M]. Oxford, England: Houghton Miflin, 1950.
　　[33] Horn B K P, Schunck B G. Determining optical flow[J]. Artificial Itelligence, 1981, 17(1): 185-203.
　　[34] Lucas B D, Kanade T. An iterative image registration technique with an application to stereo vision[C] Proceedings of the Proceedings of the 7th international joint conference on Artificial intelligence - Volume 2, Vancouver, BC, Canada: Morgan Kaufmann Publishers Inc., 1981 of Conference: 674-679.
　　[35] Brox T, Malik J. Large Displacement Optical Flow. Descriptor Matching in Variational Motion Estimation[J]. IEEE Transactions on Pattern Analysis and Machine Itelligence, 2011, 33(3): 500-513.
　　[36] BarronJ L, Fleet D J, Beauchemin S S. Performance of optical flow techniques[J]. International Journal of Computer Vision, 1994, 12(1): 43-77.
　　[37] Baker s, Scharstein D, Lewis J P, et al. A Database and Evaluation Methodology for Optical Flow[J]. Intemational Journal of Computer Vision, 2011, 92(1): 1-31.
　　[38] Papenberg N, Bruhn A, Brox T, et al. Highly Accurate Optic Flow Computation with Theoretically Justified Warping[J]. International Journal of Computer Vision, 2006, 67(2): 141-158.
　　[39] Zhigang T, Wolfgang H, Wei X, et al. Weighted root mean square approach to select the optimal smoothness parameter of the variational optical flow algorithms[J]. Optical Engineering, 2012, 51(3): 1-10.
　　[40]马虹.基于5G的视觉辅助BDS移动机器人融合定位算法[J].计算机科学, 2020, 47(S1): 631-633+652.
　　[41]邵绪强,杨艳,刘艺林.流体运动估计光流算法研究综述[J].中国图象图形学报, 2021, 26(2): 355-367.
　　[42] Bung D B, Valero D. Image processing techniques for velocity estimation in highly aerated flows: Bubble Image Velocimetry vs. Optical Flow[C]// Proceedings of the Proceedings of the 4th 1AHR Europe Congress, Liege, Belgium, 2016 of Conference. 151-157.
　　[43] Bung D B, Valero D. Application of the Optical Flow Method to Velocity Determination in Hydraulic Structure Models[C]/ Proceedings of the 6th International Symposium on Hydraulic Structures, Portland, Oregon, USA, 2016 of Conference: 240-249.
　　[44] Sun D, Roth s, Black M J. A Quantitative Analysis of Current Practices in Optical Flow Estimation and the Principles Behind Them[J]. International Journal of Computer Vision, 2014, 106(2):115-137.
　　[45] Sun D, Roth S, Black M J. Secrets of optical flow estimation and their principles[C]/1 Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA: DBLP, 2010: 2432-2439.
　　[46] Farneback G. Two-Frame Motion Estimation Based on Polynomial Expansion[C]// Proceedings of the Image Analysis, Berin, Hedelberg: Springer Berin Heidelberg, 2003: 363-370.
　　[47] Shi R, Withrich D, Chanson H. Applications of optical flow technique in air-water flows[C]/ Proceedings of the 22nd Australasian Fluid Mechanics Conference AFMC2020, Brisbane, Australia: The University of Queensland, 2020 of Conference.
　　[48] Fermiller C, Shulman D, Aloimonos Y. The Statistics of Optical Flow[J]_ Computer Vision and Image Understanding, 2001, 82(1): 1-32.
　　[49] WedelA, Cremers D, Pock T, et al. Structure- and motion-adaptive regularization for high accuracy optic flow[C]// Proceedings of the IEE 12th International Conference on Computer Vision, Kyoto, Japan: IEEE, 2009. 1663-1668.
　　[50] Tu Z, Van Gemeren C, Veltkamp R C. Improved Color Patch Similarity Measure Based Weighted Median Filter[C]// Proceedings of the Computer Vision - ACCV 2014, Cham: Springer International Publishing, 2015: 413-427.
　　[51] Tomasi C, Manduchi R. Bilateral fitering for gray and color images[C// Proceedings of the Sixth International Conference on Computer Vision (IEEE Cat No98CH36271), :, 1998: 839-846.
　　[52] Elad M, Feuer A. Recursive Optical Flow Estimation- -Adaptive Fltring Approach[J]. Journal of Visual Communication and Image Representation, 1998, 9(2): 119-138.
　　[53] Rabe C, Miller T, Wedel A, et al. Dense, Robust, and Accurate Motion Field Estimation from Stereo Image Sequences in Real-Time[C]// Proceedings of the Computer Vision - ECCV 2010,Berlin, Heidelberg: Springer Berlin Heidelberg, 2010: 582-595.
　　[54] Song X, Seneviratne L D, Althoefer K. A Kalman ilter-Integrated Optical Flow Method for Velocity Sensing of Mobile Robots[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(3): 551-563.
　　55] Buades A, Coll B, Morel J. A non-local algorithm for image denoising[C]/ Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05), San Diego, CA, USA: IEEE, 2005. 60-65.
　　[56] Liu C, Freeman W T. A High-Quality Video Denoising Algorithm Based on Reliable Motion Estimation[C]// Proceedings of the Computer Vision - ECCV 2010, Berin, Heidelberg: Springer Berlin Heidelberg, 2010: 706-719.
　　[57] Bruhn A, Weickert J, Schnorr C. Lucas/Kanade Meets Horn/Schunck: Combining Local and Global Optic Flow Methods[J]. International Journal of Computer Vision, 2005, 61(3): 211-231.
　　[58] Krahenbihl P, Koltun V. Eficient Nonlocal Regularization for Optical Flow[C]// Proceedings of the Computer Vision - ECCV 2012, Bertin, Heidelberg: Springer Berlin Heidelberg, 2012: 356-369.
　　[59] Werlberger M, Pock T, Bischof H. Motion estimation with non-local total variation regularization[C]// Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA: IEEE, 2010: 2464-2471.
　　[60] Zimmer H, Bruhn A, Weickert J. Optic Flow in Harmony[J]. International Journal of Computer Vision, 2011, 93(3): 368-388.
　　[61] Volz S, Bruhn A, Valgaerts L, et al. Modeling temporal coherence for optical flow[C]/ Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain: IEEE, 2011: 1116-1123.
　　[62] Alvarez L, Sanchez J, Weickert J. A Scale -Space Approach to Nonlocal Optical Flow Calculations[C]/1 Proceedings of the Scale- Space Theories in Computer Vision, Berin, Heidelberg: Springer Berin Heidelberg, 1999: 235-246.
　　[63] Zimmer H, Bruhn A, Weickert J, et al. Complementary Optic Flow[C]// Proceedings of the Energy Minimization Methods in Computer Vision and Pattern Recognition, Berin, Heidelberg: Springer Berin Heidelberg, 2009: 207-220.
　　[64] Wedel A, Pock T, Zach C, et al. An Improved Algorithm for TV-L1 Optical Flow[C]/1 Proceedings of the Statistical and Geometrical Approaches to Visual Motion Analysis, Berin, Heidelberg:Springer Berlin Heidelberg, 2009: 23-45.
　　[65] Mileva Y, Bruhn A, Weickert J. llumination-Robust Variational Optical Flow with Photometric Invariants[C]11 Proceedings of the Pattern Recognition, Berin, Heidelberg: Springer Berlin HeideIberg, 2007: 152-162.
　　[66] Mohamed M A, Rashwan H A, Mertsching B, et al. llumination-Robust Optical Flow Using a Local Directional Pattem[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2014, 24(9): 1499-1508.
　　[67] Aujol J-F, Gilboa G, Chan T, et al. Structure-Texture Image Decomposition- -Modeling, Algorithms, and Parameter Selection[J]. International Journal of Computer Vision, 2006, 67(1): 11-13
　　[68] Weijer J V D, Gevers T. Robust optical flow from photometric invariants[C]/1 Proceedings of the 2004 International Conference on Image Processing, 2004 ICIP“04, Singapore: IEEE, 2004:1835- 1838 Vol. 1833.
　　[69] Liu T, Shen L. Fluid flow and optical flow[J]. J Fluid Mech, 2008, 614: 253-291.
　　[70] Adelson E, Burt P, Anderson C, et al. Pyramid methods in image processing[J]. RCA Engineer, 1984, 29(6): 33-41.
　　[71] Anandan P. Measuring Vision Motion from Image Sequence[D]. University of Massachusetts, US, 1987.
　　[72] Bruhn A, Weickert J, Feddern C, et al. Variational optical flow computation in real time[J]. IEEE Transactions on Image Processing, 2005, 14(5): 608-615.
　　[73] Bung D B, Valero D. FlowCV - An Open-Source Toolbox for Computer Vision Applications in Turbulent Flows[C]/ Proceedings of the Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 2017 of Conference: 1-10.
　　[74] Corpetti T, Heitz D, Arroyo G, et al. Fluid experimental flow estimation based on an opical-flow scheme[J]. Exp Fluids, 2006, 40(1): 80-97
　　[75] CaiS, Zhou s, Xu C, et al. Dense motion estimation of particle images via a convolutional neural network[J]. Exp Fluids, 2019, 60(4): 73.