用符号以外的生活语言讲清数学概念

　　在老师的工作中，追求教学质量的提高是一个永恒的话题，并且被不断赋予时代意义。

　　其中克服照本宣科就是提高教学质量的前提。通过这个话题，结合高等数学教学体会谈谈自己的看法，企图为克服照本宣科找到一些做法。本文主要是通过对如何才能把数学概念讲明白的角度去探讨教学方法。主要的方法是：不要沉迷于对数学符号的讲解，而要用符号以外的生活语言讲解清楚数学概念，以及把教科书中精简了的表述用详尽的语言阐述清楚，把数学概念的本质表达出来.

　　一、要善于把掩盖在符号下的数学含义表达出来
　　
　　教科书的文字描述都是十分简练、严谨的，特别是数学科。数学知识是用专门的符号、语言和逻辑表达出来的，它和日常生活语言是有所区别的。数学是一门重要的科学，同时又是一种精确的语言，它的表现形式极为抽象和复杂的，有时会掩盖数学的真实内涵，并可能对数学的实际应用造成障碍。我们的学生是生活在现实生活中，他们在很多时候是很难一下子就能融通生活语言和数学专门语言的。这就需要老师要善于用学生习惯的思维方式和语言把数学知识表达出来了。

　　例如函数的概念，“假设x、y是两个变量，D是一个给定的数集，如果按照某对应法则f,当变量x在D内任取一数值时，变量y总有一个确定的数值与之对应，则称这个对应法则f为定义在D上的函数，记为y=f（x），x?D.数集D称为函数的定义域，x称为自变量，y称为因变量。”

　　对于上述定义的教学，如果老师只是把这些文字写出来、念出来，大部分学生是不能明白的。因为，在这个定义里，全是数学的语言，没有一点能摸得着，看得到的东西，没有一点是生活的气息。对于什么是“对应法则”?为什么一个法则成了一个函数？学生们肯定如坠五里雾中，混沌不清。

　　要排除这些问题，老师必需拿出具体的东西出来。要说清楚什么是“对应法则”,老师至少要举三类例子。第一，一个解析式就是一个对应法则，如2y=x+2x+2规定了每一个x都与“它的平方加上它的2倍再加上2”对应着，并且每一个x都只能与一个y对应着；第二，一个表格也是一个对应法则，如表格：【表】

　　
　　假如以上表格x代表某校某级的九个班，y代表在某次数学考试中是平均分。在这个表格里，反映出每个班与成绩的对应关系，显然一个班只与一个成绩对应；第三，图象也是一个对应法则，如：【图】

　　
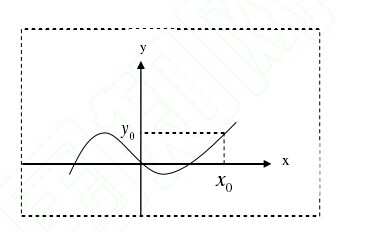
　　上述图象就规定了一种对应法则，每一个0x都有唯一的0y相对应。以上这些对应法则就是能从一个变量找到另一个变量的沟通关系。这些沟通关系就是函数。从字面意思说，“函”就是“沟通”的意思。

　　二、要从根源上把学数概念的本质揭露出来
　　
　　例如极限的概念，“设函数f在点0x的某个空心领域00U（x;d?）有定义，A为定数，若对任给的e>0存在正数d（<d?），使得当时00<x-x>d有f（x）-A<e,则称函数f当x趋于0x时以为A极限，记作00lim（）,（）xxfxAfxA?=或?（x?x）。这是大学数学系专业课教科书《数学分析》的极限定义，是一个严格的定义。

　　尽管在这个定义以前有了数列极限作为铺垫，但是如果老师在讲课时只是把定义抄到黑板上，那么任凭老师怎样声情并茂地讲解这些符号数学意义，大部分学生还是糊里糊涂的，不可能明白这个定义究竟在说什么。3在高职公共课的高等数学教材中，极限的定义有了简化，是一种描述性的概念。”设函数f（x）在点某个去心邻域00U（x,d）内有定义，如果存在常数A,当x在00U（x,d）内无限接近0x时，f（x）无限接近于A,则称A为函数f（x）当0x?x时的极限，或称当0x?x时函数f（x）收敛于A.记作00lim（）,（）xxfxAfxA?=或?（x?x）。“但是，这种定义仍然不能使学生容易理解的。

　　是什么原因产生这种现象呢？原因是中学里的数学概念、证明、计算等都是静态的，函数变量的变化是有限的。大多数的知识能跟日常生活联系起来的，所以容易理解。而现在极限的概念是动态的、变化的，函数的变量的变化是无限的，是一个很陌生的概念。具体说，有两点学生是很难理解的：第一，”0x?x“与以往的”0x=x“有什么异同；第二，极限A的意义是什么？如果不解决这两个问题，学生是很难理解极限的概念的。

　　为了解决这个问题，老师至少要做以下两步工作。第一，在讲解概念前要把极限的起源介绍一下，可以首先介绍我国古代数学家刘徽的割圆术，然后介绍牛顿求瞬时速度的极限思想。第二，更重要的要指出，因为有些很多数学问题用”0x=x“的方法是计算不出所需要的结果的，例如圆周率的推算就不能这样计算来。同样瞬时速度也不能用这种方法计算出来的。因此，我们就用”近似“的计算方法，例如刘徽计算圆周率就是这个方法，即用边数有限多的正多边形代替圆。但是”近似“始终不是精确，所以还不是完美的方法。平均速度（v）=路程差（Vs）/时间差，当时间差很少时，可以认为近似于某时刻的瞬时速度。但牛顿计算瞬时速度时已经有了超越”近似“的方法。他把”时间差（Vt）“趋于零，即如果0x是某一时刻的话，那么变化中的时间”0x?x“,这样计算出来的结果就是瞬时速度了。这个方法可以这样解释的：首先我们要明确某时刻的瞬时速度是客观存在的，时间差（Vt）越小就越接近瞬时速度，函数值（v）在变化中越向着固定的瞬时速度接近。在时间差（Vt）无限趋于零的过程中我们去寻找函数值（v）的变化趋向，当它向着一个固定的值无限接近时，这个固定的值就是瞬时速度了，这也就是极限A了。必须强调，这个极限A不是用”0x=x“代入公式”平均速度=路程差/时间差“计算出来的。而是通过”0x?x“这种无限变化找到了函数的变化的固定趋势A.是通过动态找到静态，是从此岸到彼岸的升华。这是精确值。这就是极限概念的本质。

　　通过以上这样的引言，我相信，学生是可以接受、理解极限这伟大的思想的。

　　三、要善于用生活语言把数学概念表达出来
　　
　　在《数学分析》或高职院校的高等数学教科书里，函数连续性的定义都有这样的描述的”若00lim（）（）xxfxfx?=,那么就称函数y=f（x）在点0x处连续。“这个定义很简洁、很严格，但学生听起来却很难明白。本来是一个来自生活来自具体图象的概念，在数学教科书里却变得复杂起来，这就需要老师把严格的数学概念用生活语言表达出来。

　　造成理解函数连续性概念有困难原因是概念中使用了极限概念，所以，要讲解清楚函数连续性概念的关键是把极限概念讲清楚。我认为可以按以下的步骤讲解：

　　第一，用图象把函数连续性的几种基本形式表示现来。【图1-3】

　　
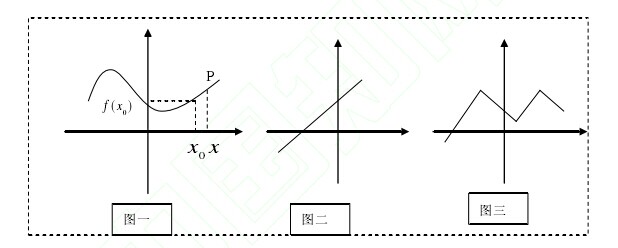
　　以上是三种连续函数的基本类型，分别是平滑的曲线、直线和折线。

　　第二，用生活语言描述函数连续性：就是连续不断，或者说，一点挨着点没有间断。以上三类图象都是连续函数。

　　第三，用生活语言解释极限的含义。以上述图一为例，点00（f（x），x）是函数内的一点，00lim（）（）xxfxfx?=的意思是，当在0x的一个邻域内的任一点x无限接近0x时，点P无限接近点00（f（x），x），也就是说，点P与点00（f（x），x）没有间断；而当x=0x时，0f（x）=f（x），也就是说，点P与点00（f（x），x）重合了。可以这样描述，在x的一个邻域内，点P可以逐步地接近点00（f（x），x），然后到达点00（f（x），x），最后通过点00（f（x），x）。即点00（f（x），x）和它两侧的点紧密联系在一起，一点挨着一点，从没有分离过。所以，点00（f（x），x）是连续的。实践证明，通过用这样的语言解释，学生是可以很快理解函数连续性概念的。

　　参考文献
　　[1]任顔波，何鹏。高等数学（经济类）[M].天津市：南开大学出版社，2004.
　　[2]华东师范大学数学系。数学分析（上册。第三版）[M]北京市：高等教育出版社，2001:42.