(二) 认知与情感的整合模型。
数学教育界接踵而来的各种研究发现,影响数学情感的因素远远超过了 McLeod (1992) 和 Hart(1989) 等界定的范围。如,数学价值观、学习者身份、数学动机、数学的社会规范[10]等都会对数学情感产生影响。数学情感概念的一再丰富,使其模型的发展走向了开放。
1. 立体数学情感模型。
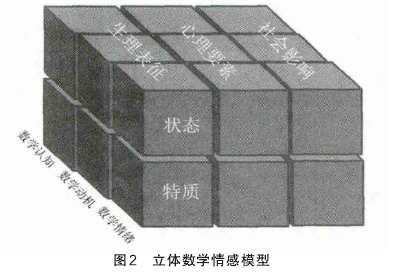
Hannula (2012) 提出了一种包含三大立体维度的“立体数学情感模型”(见图2)。[11]第一维度参照教育心理学家的研究,认为数学情感由数学认知、数学动机、数学情绪组成。第二维度由状态、特质两个因素组成。如,从情绪状态的角度看,数学焦虑是学习者正在经历的数学学习害怕感;从情绪特质的角度看,则固化为学习者在遇到类似的数学任务时,都会有产生这种恐惧的倾向。第三个维度进一步区分了前两个维度,试图从与数学情感相关的生理、心理和社会理论角度看待数学学习。
数学情感的整合型模型相对于单一型模型来说,有三个飞跃性的进展:第一,它首次将数学认知纳入数学情感模型中,突出了认知与情感之间的密切关联;第二,它跳出个体心理学界限,强调社会因素对数学情感的影响,从个体层面拓展到社会层面;第三,它试图整合与数学情感有关的基础神经学、个体心理学等理论,从而使其格局宏大、视野宽广。
2. 问题解决中的数学情绪模型。
近十年来,有研究者开始从数学情感整体模型探讨转向个别要素的深入研究,如“数学情绪”成为当前数学情感领域的一大新兴趋势。在这方面,较具代表性的是Goldin (2009) 提出的“数学问题解决中的情绪路径模型”.[12]
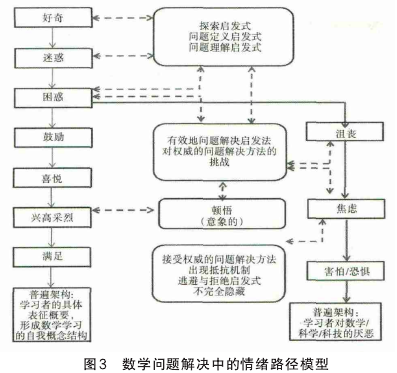
Goldin (2009) 构建了数学问题解决中的情感表征系统与认知表征系统相结合的模型。此模型将数学情感定位于一种情绪性状态,即瞬间的、变化性的情感状态。这有助于研究者捕捉学生在问题解决过程中的感受,辨别学生在储存和提取有用信息、操作监控、激发思维等方面的细节。该模型从结构的积极和消极两大路径来看学生在问题解决中所经历的数学情感 (见图3)。在图3中,实线代表的是问题解决者个体改变所发生的情感;虚线代表的是问题解决过程中个体的情感状态对启发式方法策略的影响。在此模型中,问题解决者的情感状态起源于好奇心,当问题深入的时候,他们就会产生迷惑的感觉;当迷惑持续下去,就进入困惑阶段。
许多学生到这里就停滞了,难以往下走,需要教师进行干预和帮助指导,他们才能走出难关。在教师的指导和鼓励下,学生慢慢解开疑团,疑难问题开始被分解,学生之前的困惑慢慢转变成了正向的喜悦之情。如果在教师的提示中,学生顿悟了某些节点,能给他们带来莫大的快乐。最终,他们感受到问题解决的成功和满足,为进一步解决其他数学问题奠定了良好的心理基础。反之,学生没有得到应有的帮助,他们就会产生负面情绪,持续不断的停滞不前让他们感到沮丧,此时的问题解决,就像钻进了一个死胡同一样。也许学生们在下一步会突发奇想出新的思路或方法,回到正能量主导的情绪状态中,但是不幸的话,也可能会一直纠缠在问题无法解决的沮丧当中,最终导致情感上的焦虑。如果此时还伴随着外部影响的效应,如可能受到教师的批评或者获得很低的数学考试成绩等,他们就会把这种外部刺激内化到自身的情绪状态中,最终形成害怕和恐惧,以致产生对数学及相关学科的厌恶。
三、数学情感研究对高中数学教学的启示。
从数学情感单一型模型到整合型模型的变迁,可见数学情感的研究视角从单一关注 “纯情感”的阶段过渡到了关注全局的整合性视角阶段,强调数学认知与数学情感的整合,以及数学教育中宏观与微观的整合。在新课程改革的背景下,我们应在高中数学教学中强化关注数学情感的作用,为学生的数学发展及教师的专业成长助力添彩。具体来说,数学情感研究对高中数学教学及研究带来了如下启示。
(一) 将数学情感作为数学思想方法的核心助力。
从数学教育的本质来看,数学教学除了突出知识、技能目标外,还要体现数学思考,把数学的学术形态转换为教育形态。数学教育的价值,不仅在于知识的习得,更在于逻辑与思维的培养,在于化归、递变、分类、贯通等核心思想方法的学习。因此,在今天的数学课堂中,教师不能只单纯地进行教学策略比拼,不能再仅为解决难题而苦练学科知识储备,而是要在教师与学生的充分情感联系中,对学生的数学发展需求作出专业判断,把握最恰当的时机进入到学生的数学学习过程中。
过往的实证研究已经表明,学生的学习态度、信念、自我效能感等与其数学成就间存在高相关性,数学情感变量在很大程度上影响着学生的数学成绩。[13]因此,教师是否能读懂学生的情感需求,善用他们的情感资源,提供适当的学习任务,采用理想的教学方法,完全会使学生形成不同的数学思考。[14]
那么,课程改革中教师扮演的“引领者角色”要求教师结合学生的认知情况、社会化状态等理性地对其进行干预。如,学生在数学学习中遇到了一连串尝试理解的新问题,会进入难以理解问题意思的“判定性困惑”阶段,此时教师就需要对他们进行干预。选取这个时机,是因为当学生把传统的方法策略都思考尝试了之后,仍然没有解决问题。此时,哪怕是教师一句很小的外部鼓励,像“你刚刚的思路是可以的”等,都会帮助学生打消疑虑,有信心继续解决问题。再如,学生在遇到个人无法解决的难题时,教师可以提供异质的学习共同体,帮助他们简化难度、合作解决。
总之,教师对学生的情感干预,可以促进有效教学,实现从关注数学知识转向关注知识背后的观念和思想。随着研究的发展,数学情感已从单纯的态度、信念、情绪等维度发展到宏观的环境因素、生理特征等维度,这是数学学习的非认知领域的统整,无疑对数学核心思想的形成起着重要的作用。
因此,重视学生数学情感,能有力推动数学思想方法的形成与深入。