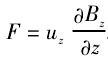 玻尔 -索末菲理论的理解上,银原子角动量磁矩等于对应电子轨道角动量磁矩,表达式为
玻尔 -索末菲理论的理解上,银原子角动量磁矩等于对应电子轨道角动量磁矩,表达式为
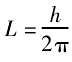 又因 cos θ = ± 1,所以前文提到了银原子磁矩在 z轴上磁矩为
又因 cos θ = ± 1,所以前文提到了银原子磁矩在 z轴上磁矩为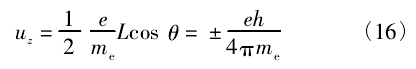
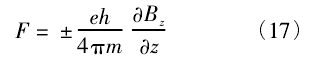
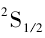 ),则磁量子数ml的取值应为 0个,说明银原子在经过不均匀磁场后不偏转,这与结果显然矛盾。
),则磁量子数ml的取值应为 0个,说明银原子在经过不均匀磁场后不偏转,这与结果显然矛盾。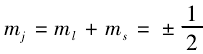 ,所以银原子的角动量磁矩就是电子自旋磁矩,即
,所以银原子的角动量磁矩就是电子自旋磁矩,即
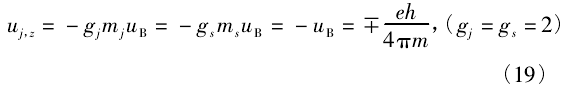

课堂实验一直是学生比较热衷的,特别是初中物理教学,自从新课程实施后,课堂实验已经在物理教学中占据了较大比重。但由于受时间限制,课堂实验实施过后对学生的学习能力提升并不明显,反而导致教师课程紧张,学生一头雾水这种尴尬局面的发生。...
伴随着新课程的全面铺开, 新课标、新教材赋予了实验教学新的内容和要求。例如, 高中物理课程标准第四部分就提出了明确要求---信息技术要进入物理实验室[1].依笔者观点, 有必要就信息技术与高一物理实验教学融合的问题加以研究, 以切实提高高一物理实验教...
初中物理是一门比较复杂的学科,不同以往的学科要求。步入初中,学生对知识的掌握更上一层台阶,掌握到更多的知识内容,可以熟练地应用各种物理公式,增强自身的创新能力。...
物理是一门自然科学,也是一门实验学科,物理学的规律都是从实验中总结、概括出来的,所以物理教学要通过实验来开展,通过实验直观地展示物理规律,验证物理理论的正确性,进而使学生逐步掌握探索自然的思想和方法,并最终达到提高学生科学素养的目的。...
初中物理教师在进行实验教学活动时,要重视学生的主体作用,创新教学模式,进而提高学生的逻辑思维能力。在课堂教学过程中,给学生创建一个轻松愉悦的课堂环境,调动学生的主观能动性,提高课堂效率,提升课堂效果。...
实验室作为诱导创造力和培养实践能力的主要场所,自形成之日起,其基本功能---实验教学则伴随着高等教育演变的几经变革,其教育价值不断地得到提升、开发和完善;而其社会功能---科学研究则在与科技、经济和社会发展的相互促进、协同发展的互动机制中...
一、认真备课上实验课应当和其他课一样备课,写教案。除此之外,教师还应该提前预做实验,以便取得第一手资料,懂得每一个实验的关键,这样才能取得主动权,做到心中有数。为了使每一位学生都能做好实验,上课前检查每一组仪器也是应该做的一项工作。而不少...
物理学是一门以实验为基础的学科,在物理学发展过程中,实验占据重要的位置。如果缺乏实验基础,物理学很难有重要发现。中国古代很多科学家提倡物理实验,主张以实验来验证自然现象,辨别事物的真伪。据我国东汉时期的王充在其着作《论衡乱世篇》记载:此尚...
兴趣是最好的老师, 在兴趣的带领下, 学生能更好地开放自己的思维, 积极自主地寻找问题的答案。对于初中二年级的学生来说, 他们刚刚接触物理, 还没有在脑海中形成一定的物理逻辑。...
0引言物理学史与物理实验教学结合在一起,是国内外教育改革的一项重要课题。传统物理教学对科学知识建构的过程和科学方法教育没有给以足够的重视,影响了学生的兴趣、态度、情感和创造力的培养,不利于学生理解科学本质,不利于培养学生的科学精神和创造力...