结合PMI和PPI指数建立新的GDP预测模型及其实证分析

　　0 引言

　　GDP（即国内生产总值）是一个国家或地区在某一既定时期内生产的所有最终物品和劳务的市场价值，能够反映出一个国家或地区经济发展状况。对GDP进行科学预测，对政府部门做出经济发展战略目标和宏观经济政策有着重要意义。

　　PMI即采购经理指数，是快速及时反映市场动态的先行指标，它由五个扩散指数的加权组成，包括：新订单、生产、就业、供应商交付和库存指数。为了使指数权重以最大限度地提高该指数与GDP增长的相关性，经过多次修改，PMI 各指数的权重保持固定：新订单（0.3），生产（0.25），就业（0.2），供应商交付（0.15），库存（0.1）。目前，全球已有20多个国家（或地区）建立了PMI编制和发布体系，美国是最早建立PMI指标体系的国家。2005年4月底，我国在北京和香港两地首次发布了“中国采购经理人指数”,其包括制造业和非制造业，中国制造业采购经理指数体系共包括11个指数：新订单、生产、就业、供应商配送、存货、新出口订单、采购、产成品库存、购进价格、进口和积压订单。

　　PPI即生产者物价指数（亦称工业品出厂价格指数），是一个用来衡量制造商出厂价的平均变化的指数，作为统计部门收集和整理的若干个物价指数中的一个，市场敏感度非常高。同时PPI也是衡量工业企业产品出厂价格变动趋势和变动程度的指数，是反映某一时期生产领域价格变动情况的重要经济指标，也是制定有关经济政策和国民经济核算的重要依据。

　　国外对PMI的研究相对比较深入，采用了很多定量分析方法。Rolando F. Peláez[1]阐述了PMI并不是最优的加权指标，进而根据美国供应管理协会提出的扩散指数复合成了一个新指数。在预测实际国内生产总值、工业生产增长率和商业周期转折点方面，它的一致性与PMI相同，但是及时性优于PMI.Danny I. Cho[2]等认为PMI的作用是预测经济的变化趋势，但是他也认为现有的PMI不是最优的加权指数，因此利用现有数据对PMI进行了重新加权，重新加权后的PMI与GDP的相关性优于原有PMI.AnthonyJosepha[3]认为利率和PMI的历史值是PMI预测的有效因子。基于此用神经网络模型预测PMI得到的大部分评价指标值都优于回归模型预测得到的指标值。Evan F. Koe-nig[4]讨论了PMI的作用是预测制造业的增长、经济的拐点和美联储政策的变化。研究得出结论：一般PMI高于47表明制造业在扩张；预测GDP的临界值在40左右；PMI值如果高于52.5往往要上调短期利率。Matthew D. Lindsey[5]等试图通过跟踪和预测PMI的转折来洞察一般商业周期，利用PMI12到65个月的固有周期建立回归模型，来预测PMI的转折点和一般商业周期的变化。国内关于PMI的研究以定性较多，多是针对PMI的变化来预测中国各方面经济将会产生什么样的变化。关于PMI的定量研究论文较少，尤建新[6]认为对采购经理进行调查得到的PMI数据从理论上讲能够反映市场的变动情况，把CFLP-PMI各个细分指数与宏观经济统计数据进行对比，与行业统计数据进行对比，均显示一定的相互关联或者一致性，得出CFLP-PMI可以作为决策参考的结论。

　　本文从建立一个预测效果优于PMI的GDP预测模型出发，结合PMI和PPI指数建立了一个新的GDP预测模型，然后将这个模型与单纯用PMI做自变量的预测模型和Rolando F. Peláez[1]的改进模型做拟合效果和预测效果的对比，来验证新模型的优劣。

　　1 研究设计

　　1.1 数据来源

　　研究样本数据来自于中国国家统计局网站，采用2009年第3季度到2012年第1季度的数据，包括实际GDP的季度增长率，PMI及其五个扩散指数（新订单，生产，就业，供应商交付和库存），PPI的同比增长率。其中PMI、五个扩散指数及PPI的同比增长率是月度数据，用加权平均的方法得到季度数据。PMI中没有直接反映价格的指数，然而价格指数在经济中是很重要的反映经济变化的参数，所以加入PPI指数，试着发现价格对GDP的影响。

　　1.2 模型设计

    论文提出的模型是基于各指数之间的相关性得出。

　　在选择模型的自变量时，去掉指数之间相关性强但与因变量相关性弱的指数。张利斌、冯益[7]研究了 PMI 与GDP的关系，得出PMI领先于GDP走势3到12个月，最好的预测效力是3个月，因此建立模型时各个指数分别滞后3个月也就是1个季度，其中PPI也是先行指标之一，滞后1期与GDP的相关性较高。各指数的相关性如表1所示。
 

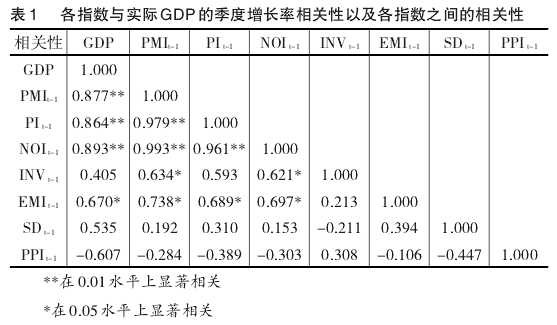
　　从表1可以看出，新订单指数（NOI）与生产指数（PI）之间的相关系数为0.961,两个指数之间有非常强的相关性，完全可以相互替代。库存指数（INV）与生产指数和新订单指数的相关系数（分别为0.593和0.621）大于其与GDP的相关性（0.405），就业指数与新订单和生产的相关性（分别为 0.738,0.689）高于其与 GDP 增长率的相关性（0.670）。表明就业指数与新订单和生产指数之间都有较强的相关性。通过分析，选定的模型如式（1）所示。

　　Gt=α0+α1NOIt-1+α2SDt-1+α3PPIt-1+et（1）。

　　其中Gt是中国实际GDP的季度增长率，NOI表示新订单指数，SD表示供应商交付指数，PPI表示生产者物价指数的同比增长率。模型1包含新订单指数，供应商交付指数和PPI指数。

　　为了比较提出的模型的预测效果，论文给出了两个比较模型：第1个是实际GDP的季度增长率与现有固定模式的PMI关系的模型；第2个是Rolando F. Peláez[2]提出的针对美国经济的相对最优模型。如式（2）和式（3）所示。

　　Gt=α0+α1PMIt-1+et（2）。

　　Gt=α0+α1NOIt-1+α2EMIt-1+α3SDt-1+et（3）。

　　其中EMI表示就业指数，模型2是滞后1期的PMI与实际GDP季度增长率的关系模型。模型3包含新订单指数、就业指数和供应商交付指数，这个模型是基于美国经济情况对PMI的改进模型。

　　2 实证分析

    2.1 模型比较

    采用2009年第3季度到2011年第3季度的样本数据集，使用软件Eviews[8]对式（1）-（3）进行多元线性回归分析，所得模型估计结果如式（4）、（5）、（6）所示。

　　Gt=-20.66+0.24NOIt-1+0.35SDt-1-0.06PPIt-1（4）。

　　Gt=-18.17+0.53PMIt-1（5）。

　　Gt=-35.55+0.30NOIt-1-0.18EMIt-1+0.76SDt-1（6）。

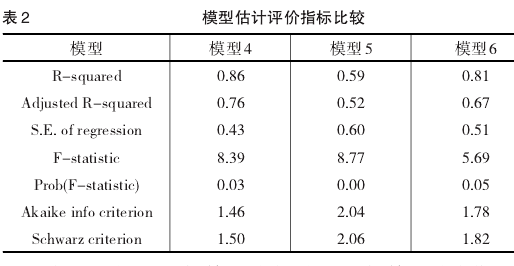
　　表2是由2009年第3季度到2011年第3季度期间数据做最小二乘法估计后整理得到的结果。从 F 检验值（F-statistic）及其相伴概率（Prob（F-statistic））来看，三个模型的相伴概率分别是：0.03、0.00、0.05,说明3个三个模型都具有显着性；从 R 平方和调整的 R 平方（AdjustedR-squared）来看，三个模型的调整的R平方分别是：0.76、0.52、0.67,显然模型4拟合程度较好于模型5和模型6;从标准估计的误差（S.E. of regression）来讲，模型4的误差为0.43低于模型5和模型6（分别为0.60和0.51）；三个模型的赤池信息准则（Akaike info criterion）即AIC准则的值分别为：1.46、2.04、1.78,可以看出也是模型4较好；表中施瓦茨准则（Schwarz criterion）即SC准则，很显然可以看出模型4（1.50）优于模型5（2.06）和模型6（1.82）。综上所述，从模型估计效果来看，模型4是三个模型中最优的。模型4优于模型5,说明PMI不是最优加权的GDP预测指标。模型4优于模型6说明依据美国经济情况优于PMI的预测模型，虽然在中国经济情况下也优于PMI预测模型，但是相比之下模型4更好一些。

　　2.2 模型检验

　　根据以上研究模型4的拟合效果较好于模型5和模型6,但是拟合效果好，不一定预测效果好。因此，分别用模型4、模型5和模型6预测2011年第4季度和2012年第1季度的GDP季度增长率，来检验3个模型的预测效果，结果如表3所示。

　　由表3可知，2011年第4季度和2012年第1季度的实际GDP季度增长率分别为8.9和8.1.首先比较3个模型对2011年第3季度GDP增长率的预测值，模型4、模型5和模型6的预测结果分别为8.99、8.81和8.63,从数值来看，模型 4 和模型 5 优于模型 6.模型 4、模型 5 和模型 6 对2012年第1季度预测结果分别是8.17、8.28和8.74,明显可看出模型4的结果比较好。其次比较3个模型的评价指标，RMSE即均方根误差（Root Mean Squared Error）和MAE平均绝对误差（Mean Absolute Error）取决于因变量的绝对数值，通常更直接查看的相对指标是MAPE即平均绝对百分误差（Mean Abs. Percent Error）。表中三个模型的平均绝对百分误差分别为：2.68、4.16、2.85,可以看出三个模型的预测精度都较高。从Theil Inequality Coefficient即希尔不等式系数，三个模型的值分别为0.015、0.026、0.017,从这个指标来看模型4的预测精度高于其他两个模型。Bi-as Proportion是偏差率，Variance Proportion是方差率，Co-variance Proportion是斜变率，当预测比较理想时，均方误差大多数集中在斜变率上，偏差率和方差率都很小，三个模型的斜变率分别为0.96、0.87、0.95,所以模型4的预测是三个模型中最理想的。所以总的来说模型4的预测效果最好。

　　综合以上对模型估计和预测效果的分析，一致得出模型4优于模型5和模型6.模型4能更好地反映经济发展的走势，使GDP在预测中得到可信度更高的预测值。

　　3 结论

　　论文首先根据参考文献以及指数间的相关性设计模型，其次对模型利用最小二乘法进行估计并根据模型拟合效果评价指标进行比较，最后通过实证分析，选用对2011年第4季度到2012年第1季度的数据进行预测，来检验选出的最优模型的预测效果。实证分析表明新的GDP预测模型的效果优于仅用PMI预测GDP的效果。

　　论文从考证PMI的组成结构角度出发，结合其在预测GDP中的重要作用，对其进行重新评估，并且加入重要的反映价格的指标PPI,建立新的预测模型，从而改善了单纯用PMI对GDP预测的效果。未来可以综合各个宏观经济先行指标对实际GDP的增长率做更精确的预测。

　　参考文献：

　　[1]Rolando F.Pelaez: a Reassessment of the Purchasing Managers'In?dex [J].Business Economics,2003,（12）。
　　[2]Danny I.Cho, Tomson Ogwang. Conceptual Perspectives on Selectingthe Principal Variables in the Purchasing Managers' Index [J]. TheJournal of Supply Chain Management, 2006,42（2）。
　　[3]Anthony Josepha, Maurice Larrainb, Claude Turner. Forecasting Pur?chasing Managers'Index with Compressed Interest Rates and PastValues [J]. Procedia Computer Science, 2011, （6）。
　　[4]Evan F. Koenig. Using the Purchasing Managers'Index to Assess theEconomy's Strength and the Likely Direction of Monetary Policy[J].Economic & Financial Policy Review, 2002, 1（6）。
　　[5]Matthew D.Lindsey, Robert J.Pavur. As the PMI Turns: a Tool for Sup?ply Chain Managers [J]. The Journal of Supply Chain Management,2005,41（1）。
　　[6]尤建新。中国采购经理指数的研究与应用[J].中国科技论坛，2006,（6）。
　　[7]张利斌，冯益。中国PMI与GDP关系的实证检验[J].统计与决策，2012,（2）。
　　[8]易丹辉。数据分析与EVIEWS应用[M].北京：中国人民大学出版社，2008.