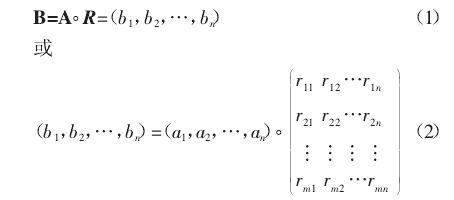0 引言
当前医院论证、选择、购置医疗设备,一般是由主管领导、医院设备科和使用人员经过市场调研,依据经验来决策。较正规的方法是行政会议决定、专家定性评议、科室评议、市场调查等方式,但是难免出现偏颇[1].模糊数学,即使用数学方法去探讨、研究和处理包含“模糊性”现象的实际问题[2-3].其中,“模糊性”定义为客观事物之间差异的中间过渡界限的“不分明性”.医疗设备购置决策往往无法用量化的数值来描述,而只能用客观或主观模糊的原则进行推断或判定。本文中我们利用模糊数学方法和原理,来探讨和研究如何有效地综合评判购置医疗设备决策。
1 综合评判的数学模型
设定对象评价时包含m个因素,其集合为:U={u1,u2,…,um},其中,u表示因素。n个评语的集合为V={v1,v2,…,vn},其中,v表示评语。根据医疗设备购置决策的原则,评语集合一般可取为V={优秀,良好,中等,合格,不合格},也可选取其他的评语集合[4-5].如果定义rij为第i个因素对第j种评语的隶属度,则U与V之间的模糊性关系R可表示为

其中,r为隶属度元素。0≤rij=uR(ui,vj)≤1,i=1,2,…,m;j=1,2,…,n.进行评价之前,应确定各种因素的权重比例,即加权,A可视为因素权重集合,记作:A=(a1,a2,…,am),0≤ai≤1,i=1,2,…,m.在统筹兼顾各种因素的情况下,A和R的模糊变换是对待评对象作出的最终评判,该过程称为模糊综合评判。模糊综合评判的数学模型可表示如下:
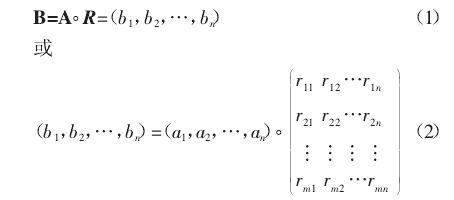
其中,a为评价权重元素,r为隶属度元素,B为模糊综合评判集合,“莓”为模糊运算符。上式采用特殊符号,广义模糊运算下,待评对象bj的计算公式为



 2 模糊综合评判数学模型的实质
2 模糊综合评判数学模型的实质
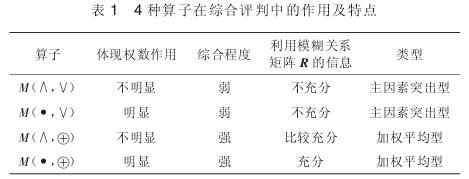
前文中提到的4种模糊算子有不同的作用,体现权数的作用不同,综合程度强弱也不同,利用因素权重集合A的信息程度也不相同,4种评判模型代表着不同的综合评判类型。应用综合评判模型论证采购医疗设备的流程是一样的。模糊综合评判的流程图如图1所示。
模糊综合评判的过程B=A莓R=(b1,b2,…,bn)是输入因素权重集合A,经模糊关系矩阵R后,输出模糊综合评判集合B.由于A决定计算结果,因此必须正确认识A的实质,才可获得合理的评判结果。广义模糊运算下的综合评判的一般模型即式(2)中,只考虑ui时,rij为ui的评价对等级vy的隶属度。因此,ai*rij就是在全面考虑各种因素时,ui的评价对等级vy的隶属度,即rij=ai*rij就是对隶属度rij的修正。而广义的“或”运算*+即对各个已修正的隶属度rij进行综合处理,以争取公正合理的综合评判。4种算子在综合评判中的作用及特点见表1.
总之,综合评判结果是否客观,取决于A.而应用模糊数学法的关键是建立符合实际的隶属函数。
3 模糊数学法在医院设备购置中的具体应用
模糊评判指标的确立、加权指标的分配、数学模型的选择、评选标准的确定等都应由设备购置论证小组公开讨论商议决定。该方法采用科学的数学方法量化复杂的模糊概念,对医疗设备购置决策进行量化描述,为了公正,可从院领导、相关专家、医务人员、设备使用人员、设备采购人员、医学工程人员中各选取几个成员组成论证小组,以确保论证结果的质量[9].医院设备购置中,模糊数学法的实现过程如图2所示。
4 模糊数学法采购医疗设备的实例
在实际应用中,我院从实际出发,确立评判指标、等级、权重等。利用上述方法,我们对医院一些设备的采购进行量化考评,获得了可观的结果。下面以心电监护仪的采购为实例,阐述模糊数学评判模型在医院设备采购中的应用。
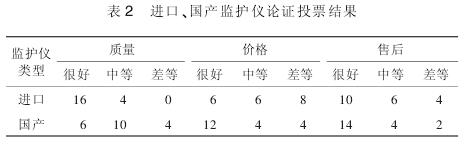
我们选取武汉市区三甲医院的20名专家进行投票,模糊关系矩阵R1为进口监护仪,R2为国产监护仪。进口、国产监护仪论证投票结果见表2.
(1)论证采购进口或者国产设备:①确立产品评判指标集合X,包括质量、价格1售后服务。②将评判等级分成3级。③明确模糊关系矩阵R.④确立权重系数W .医疗设备的质量是医疗设备采购考虑的重点,经论证小组讨论W=(0.5,0.2,0.3)。⑤实施综合评判。进口监护仪模糊综合评判集合B1=W莓R1=(0.5,0.2,0.3)莓R1=(0.61,0.25,0.14),B2=W莓R2=(0.5,0.2,0.3)莓R2=(0.48,0.35,0.17)。⑥确定设备评判标准。通过论证小组商定,加权系数定为F=(0.5,0.2,0.3),最终评判结果进口监护仪C1=B1莓F=(0.61,0.25,0.14)莓F=0.397,国产监护仪C2=B2莓F=(0.48,0.35,0.17)莓F=0.361.由上述数据可知C1>C2,即应该采购进口品牌监护仪。
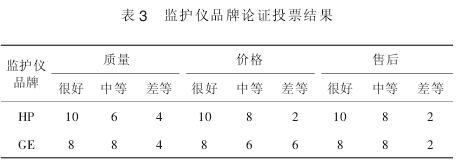
(2)选定了进口产品后,应用模糊数学法论证选择进口品牌的厂家,有美国GE和HP公司2家参加竞争。论证小组在分别同2家公司洽谈的前提下,采取上述方法对它们的产品进行投票,结果见表3.
按同样方法计算可得:B1=(0.5,0.35,0.15),B2=(0.43,0.38,0.19),CHP=B1莓F =0.365,CGE=B2莓F =0.348,由于CHP>CGE,最终遴选出美国HP公司。
5 结语
医疗设备,尤其是高端医疗器械,若购置选型得当能够确保医院设备的正常运行和高效使用,优化购置资金的配置。同时,新决策和评判方法的引入,可提升医院的设备管理水平。在实际应用中,可以采取模糊数学法对医疗设备购置进行量化考评,各医院可依据各自的现实情况,确立评判权重、指标、等级等,具体评判标准可能略有不同,需由采购医院来制定。本文中应用的方法对各设备采购的评判较为全面,采取量化考评方法,用客观实在的数据来决策,可有效防止设备采购独裁,其他设备的采购也可使用类似方法。
[参考文献]
[1]李斌,何梦乔,曹建文。当前医疗设备采购的SWOT分析与战略思考[J].中国医疗器械杂志,2006(3):206-208.
[2]张丽芳。浅谈医疗设备采购中常见的问题及对策[J].中国政府采购,2014(1):53-54.
[3]杨坤,邵蕾。大型医院医疗设备采购流程精细化管理的探讨[J].生物医学工程学进展,2014(2):108-111.
[4]程乾生。质量评价的属性数学模型和模糊数学模型[J].数理统计与管理,1997(6):18-23.
[5]谢季坚。模糊数学方法及其应用[M].武汉:华中科技大学出版社,2013:11-50.
[6]杨纶标,高英仪,凌卫新。模糊数学原理及应用[M].广州:华南理工大学出版社,2011:18-23.
[7]姚炯,丁丽萍。模糊数学在医疗质量综合评价中的应用[J].中国卫生统计,2000,17(1):44-45.
[8]胡宝清。模糊理论基础[M]. 2版。武汉:武汉大学出版社,2010:20-46.
[9]吉利侠。医疗设备采购评标中模糊综合评判分析模型的研究[J].中华生物医学工程杂志,2013,19(1):69-72.