0引言
采矿工程工作的顺利开展离不开采矿方法的正确选择,其选择正确与否对全面提高矿山的生产能力、安全保障能力和经济效益起着决定性的影响,也直接影响着采矿生产对环境的破坏程度。因此,选择一种科学合理的采矿方法显得尤为重要,然而,采矿方法的选择常常会涉及不同层面、服从多种指标、需要考虑众多复杂因素,很容易受不确定因素的影响。目前采矿方法的选择绝大多数还是依靠传统的工程类比法,这种方法存在极大的主观随意性,面对诸多不确定的因素,只能用定量指标进行分析比较,无法定性分析,使采矿方法选择具有很大的不确定性、模糊性和随机性。
随着研究的不断深入,模糊数学已在矿山建设很多方面得到了广泛的应用,对复杂事物和复杂系统可以进行模糊度量、模糊识别、模糊控制和模糊决策等[1].然而,这种原理很少应用于采矿方案的优选,并且由于仅利用模糊数学理论无法确定复杂的指标体系的权重,权重只是通过专家的主观评审选取,带有一定的主观性,因此需要引入新的方法。层次分析法能够将定性分析与定量分析相结合,把多目标、多准则、复杂的问题分解为若干层次和若干因素进行分析,是确定权向量行之有效的方法。本文综合分析并选取影响采矿方法选择的4个方面的因素,将层次分析法和模糊数学各自的优点相结合,利用模糊数学量化各采矿方法的评价指标进行多目标决策,通过层次分析法确定各因素的重要程度,建立模糊综合评判模型,从而对采矿方法进行最优选择。以探索出一种科学可行、实用性强的采矿方案优选方法。
1层次分析法确定权重向量
层次分析法是一种定性与定量相结合的系统分析和决策的方法。利用此方法,决策者通过将复杂问题分解为若干层次和若干因素,在各因素之间进行简单的比较和计算,就可以得出不同因素的权重。针对影响采矿方法选择不同属性的因素,需要运用层次分析法对决策中各因素进行权值分配。
1.1 建立评价指标体系层次结构模型
采矿方案评价涉及到众多复杂因素,指标体系中不同属性的因素之间很难直接进行比较,因此,需要把复杂问题条理化、层次化,建立一个有序的层次结构模型。通过比较分析,并根据指标选取以少量、最主要和最全面的原则[2],最终确定影响采矿方案选择的3个评价准则及各自下属9个评价指标。见图1.
1.2 构造判断矩阵
(1)建立比较标度
确定各层次因素后,需要确定两两因素相比的判断值,这里利用uij表示对于上层某因素Ak而言,下层因素Ui的重要程度的判断值。为了使评价因素的相对重要性加以定量化,这里取1-9及它们的倒数作为标度值[3],其表示含义见表1.
(2)构造判断矩阵及单排序
根据层次结构模型,参考相关资料,并通过专家组采用表1中的标度对采矿方法影响因素的重要程度进行评价,构造判断矩阵D有

为了得到相对于上一层某因素而言本层次与之有关联系的因素的重要性次序的权重,需要对得到的判断矩阵D进行排序[4].这就需要计算判断矩阵D的最大特征根λmax及对应的特征向量。最常用来进行单排序的方法有特征根法、方根法和积合法,由于在讨论采矿方法选择中元素的个数较多,计算判断矩阵的最大特征值的工作量会很大,因此这里选择一种简便的方法进行单层次排序,即积合法,具体计算方法如下[5-6]:


1.3 判断矩阵的一次性检验
由于实际问题的复杂性和不确定性,尤其是涉及的因素特别多时,很容易引发错误的决策。因此对所构造的判断矩阵进行一致性检验,确保判断的结果更好地与实际相吻合,具体方法是:
先计算判断矩阵的最大特征根λmax及一致性指标CI=λmax-n/n-1,再计算一致性比例CR=CI/RI,其中RI是平均随机一致性指标,它与n有关,具体由表2给出。当CR≤0.1时,认为判断矩阵具有“满意一致性”,是可以接受的;否则(CI≥0.1时),需要对判断矩阵作适当修正[7-8].
2 模糊综合评判
模糊综合评判是综合考虑多种因素影响的事物或系统对其进行全面和定量的评价,具有结果清晰,系统性强的特点,能够较好地解决模糊的、难以量化的问题,比较适用于解决采矿方案评价涉及到的非确定性因素,可以有效地提高判断与决策的准确性[9].其主要包括4个关键要素:因素集U、方案集V、综合评价矩阵B和权重集W.
2.1 建立评判对象的因素集U和方案集V
设评价对象的因素有m个,它们构成一个因素集U={u1,u2,…,un},根据实际情况设计出n个备选方案,组成方案集V={v1,v2,…,vn},也可以表示成m维向量形式,即:Vj={xj1,xj2,…,xjn},其中xjk(k=1,2,…,m)是从方案Uj到因素Xk上的模糊映射。
2.2 确定权重集W
依据上述的层次分析法可得到权重集W,因素的权向量为W=(w1,w2,…,wm),可以表示为因素集U上的一个模糊子集。wi为因素ui(i=1,2,…,m)在总评价中的影响程度,并且规定
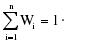
2.3 构造综合评判矩阵
由所有评价指标分属于各评价等级的隶属度值可构成模糊评价矩阵R[10].这里可以参照“隶属函数的确定方法”来确定综合评判矩阵,通常所用来确定隶属函数的方法有Delph,模糊统计法,线性函数法,二元对比排序法,增量法等,为了使计算更便捷,尽量用不同的计算方法来处理不同属性的指标。
(1)定量指标隶属度的计算
定量指标包括正指标和负指标,对于正指标,值越大越好,如采场生产能力;对于负指标,值越小越好,如采充总成本和矿石损失率。可以采用线性函数法确定其隶属度[11],计算公式为
rij=xij/Xmax(5)
xij=1-xij/xijmax(6)
式中,rij为i方案j因素的指标值;xijmax为i因素的最大指标。其中,式(5)适用于正指标,式(6)适用于负指标。
由此,可得定量指标的隶属矩阵:

(2)定性指标隶属度计算