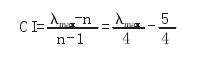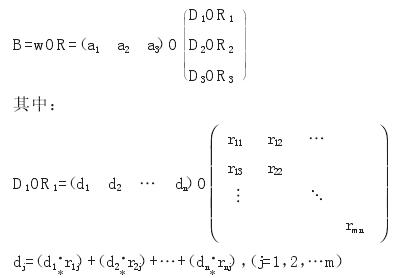引言
在日益激烈的经济竞争中,企业不但要有先进的科学技术作为竞争手段,先进的管理同样可以使的企业能够在竞争中利于不败之地。企业的管理可以提高工作效率,是企业长足发展的重要途径,而企业的预算控制模式更体现出企业的合理性与前沿性。企业依据战略导向和财务导向进行财务预算,不同企业不同时期所采取的财务预算控制模式有所不同。我国企业当前采用的预算模式主要分为:集权预算模式、分权预算模式、折中预算模式(混合预算模式),三种财务预算控制模式有各自的优缺点及适用范围。在以往研究中,虽然学者提出了预算控制模式的优劣,但是对于量化的评价研究却很少。本文依据前沿的研究选取指标,通过模糊数学方法构建对预算控制模式的数学评价,从而把三种预算控制模式的评价以量化表示。
一、财务预算控制模式评价指标
预算控制的模式反映了母公司对子公司的控制,主要体现在财务控制和决策权的控制。母公司通过财务控制实现对子公司的控制,并给予子公司一定的活动范围。这样通过财务预算实现集团的协调,实现集团利益。集权控制模式是母公司对各个子公司的财务进行严格控制统一管理,决策权高度集中母公司。分权控制模式是母公司给予子公司权利,母公司只进行监督和审核。折中式控制模式是母公司与子公司同时参与财务预算和决策,形成上下信息的互动沟通。
本文将从五方面对财务预算控制的三种模式建立评价体系,分别对集权、分权、折中进行量化分析,建立的指标(如表 1 所示)。
二、指标的权重确定
本文通过层次分析法,对指标进行两两之间相互比较,通过判断矩阵进行计算指标的权值。层次分析法特点是思路简单、层次分明、使用范围广等,算法的核心是权重的计算,特别适用于多方案问题、复杂系统的决策问题,是将问题转化成定量研究的数学方法。
(一)构造判断矩阵
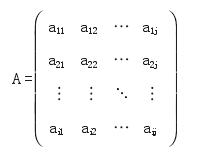
通过比较两者的相对重要性来构造判断矩阵。例如,取两个指标进行重要性比较用 aij表示,那么所有的因素进行比较之后可以得到判断矩阵 A.其表示如下:
aij两者比较的重要性用量化值描述,用 1-9 数字进行描述,数字代表的含义如下:
由以上方法对五方面的指标是否有利于实现整体利益最大化、是否有利于企业的发展战略、是否有利于降低企业的财务风险、能否发挥子公司的潜在活力、是否有利于母子公司之间的协调进行两两比较,得出判断矩阵如下:
(二)权向量和最大特征计算
首先,将一级指标的判断矩阵进行列向量归一化;其次,按行求和再次进行归一化,可得到权向量。根据特征值与特征向量关系可以求解特征值,实现方法如下:

即求得一级指标的权向量为:
w=(0.196 0.097 0.192 0.119 0.395)
(三)一致性检验
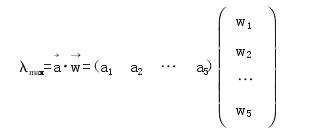
求得矩阵 R1的最大特征值λmax,其计算方法如式所示:
计算一致性指标 CI,其计算方法如式所示:
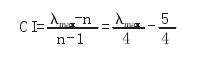
式中,n 代表指标的个数,所以对判断矩阵来说 n=5,计算一致性比率 CR,其计算方法如式所示:
CR=CI/RI
其中,RI 代表 Random Consistency Index 值(如表 3 所示)。
当 CR≥0.1 时,认为判断矩阵的不一致性不可接受。当CR<0.1 时,判断矩阵的不一致性在可接受的范围之内。当 CR=0.076<0.1 时,所以判断矩阵通过一致性检验,表明指标的权重是可以取得。
(四)评价体系指标权重
三、控制模式的模糊评价
(一)模糊数学
模糊数学概念是 1965 年查德(L.A.Zadeh)教授提出的,模糊数学对应的是精确数学,它通过非精确的计算找出隐私之间的模糊关系。模糊综合评价应用模糊理论,通过确立指标度评语的隶属度,确定评价结果的一种方法。
1.建立评价对象的因素论域 U,U=(u1,u2,…,un)。
2.确定论域中因素的定性评价语的等级 V,V=(v1,v2,…,vn)。
从专家角度将评语设定为非常有利、比较有利、有利、一般、不利,分别指某种财务预算控制模式对指标的影响,为便于计算,评语分别对应 10 分、8 分、6 分、4 分、2 分五个等级。
3.通过因素对应评语论域的隶属度 rij,建立模糊关系矩阵 R.其中:
rij=专家总人数中评价某因素某等级的人数/专家总人数
将三个准则下的指标隶属度构成三个隶属函数矩阵,矩阵形式:
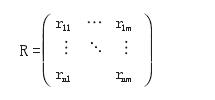
其中,rij表示指标对于评语等级论语中的隶属度。
(二)建立模糊矩阵
对指标进行专家评分后整理得到三个模糊矩阵分别(如表6 至表 8 所示)。
(三)评价结果
通过以上办法计算可以得到向量 w.将 w 和 R 利用合成算子 M(·,茌)合成得到综合评价的最终计算结果,向量表示为 B=(b1,b2,…,bm)。
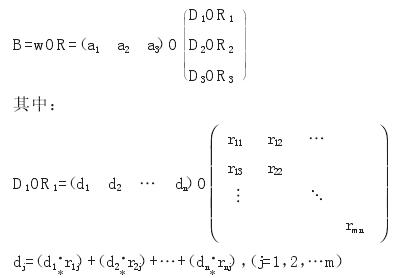
对于财务预算控制的集权模式计算结果为(0.322 0.2700.221 0.151 0.035),分权模式的计算结果为(0.268 0.192 0.1620.134 0.234),折中模式的计算结果为(0.349 0.220 0.1580.225 0.059)。
以上结果即是财务预算控制模式对企业集团发展模糊综合评价结果,其显示出,折中模式非常有利于集团发展的程度为 0.349,集权模式非常有利于集团发展的程度为 0.322,而分权模式非常有利企业发展的程度为0.268.因此,综合来看三种模式中折中模式是较好的财务预算控制模式。
结论
通过本文的模糊矩阵得出结论,集权模式更有利于实现集团整体利益(0.39)、降低财务风险(0.37)和有利于企业战略发展(0.37);分权模式更有利于子公司发挥潜能(0.49),激发子公司的创造性。折中模式的数据显示较为温和,是集权和分权的结合,但是在 5 个因素中对于企业的战略发展是最有利的(0.39)。
综合评价下,折中控制模式综合得分为 0.349,三种模式中最高,折中的财务控制模式更好地符合企业的财务预算管理。因此,企业采用折中财务控制模式更有利于企业整体的发展。
参考文献:
[1]李玲。关于企业财务预算控制模式的探讨[J].时代经贸,2008,(6)。
[2]向敏。关于我国企业财务预算控制的思考[J].学术交流,2012,(12)。
[3]徐国兵。基于公司财务目标的财务预算控制模式建构[J].财经界:学术版,2011,(8)。
[4]任纪霞。基于控制论的企业财务预算管理分析[J].财会通讯:综合版,2014,(5)。
[5]曾伟。企业财务预算管理现状与对策分析[J].商场现代化,2013,(27)。
[6]梁非坤。企业财务预算控制模式研究[D].武汉:武汉理工大学,2006.
[7]邹斐。浅析企业财务预算控制存在的问题及对策[J].经济论丛,2011,(6)。
[8]张桂南。浅析现行财务预算控制模式的发展趋势与改进方向[J].现代经济,2008,(5)。
[9]田艳。我国集团公司财务控制模式研究[D].南京:南京航空航天大学,2008.
[10]潘露兰,李正明。中小企业财务预算控制问题研究[J].中小企业管理与科技旬刊,2014,(32)。