模糊数学在桥梁检测中的影响研究

　　摘要：伴随着我国经济社会的迅猛发展, 桥梁工程以占取略小的空间从而实现极大的交通过往, 成为我国经济建设中重中之重。然而在取得骄人成绩的同时, 建设过程中存在的问题随着时间的积累逐渐的暴露出来, 公路桥梁安全质量事故也开始进入人们的视野。本文通过在桥梁检测中对影响桥梁安全的众多因素进行模糊数学研究, 可以准确的得出该桥梁整体安全状况, 为桥梁后期运营及加固提供科学依据。

　　关键词：模糊数学; 桥梁检测; 模糊测度;

　　桥梁的安全性更多指的是桥梁具备的一种能力, 众所周知桥梁会承受恒载、荷载、以及其他荷载等等, 桥梁的安全性就是在这些荷载作用下依旧可以正常工作不造成事故的能力。桥梁检测的目的就是对桥梁进行安全评定并找到桥梁的缺陷和损失的主要原因。桥梁检测是消除交通安全隐患, 测试桥梁承载力的有效途径, 是获得桥梁实际工作状态的唯一方法[1]。

　　1 模糊数学

　　1.1 模糊数学的背景

　　生活中的许多事物, 都或多或少的存在着模糊性和混淆不清的性质。“模糊”的概念是最微妙和难以捉摸的, 但往往是熟悉的, 最重要的, 但它有一个非常明确的定义在现代数学。但是所为"模糊”有两种含义, 一是恍似关系、一是佛似关系[2]。模糊理论的概念强调用模糊逻辑来描述现实生活中事物的层次, 以补偿古典逻辑 (二值逻辑) 不能对不标准定义事物边界进行描述的缺点。人类的语言在表达上很模糊。用“是非”、“好”或“坏”来描述世界的科学问题是不可能的。模糊理论定义模糊、模糊集、事件 (事件) 的概念属于这一组层次 (成员) , 并得到量化和量化级别 (成员) , 来处理问题[3]。

　　1.2 模糊综合层次评判法

　　FAHP评价法是一种将模糊综合评判法 (Fuzzy Comprehensive Evaluation, FCE) 和层次分析法 (Analytic Hierarchy Process, AHP) 相结合的评价方法, 在评价体系中, 绩效评价有着广泛的应用, 系统优化、评价的定性和定量模型, 一般是首先用层次分析法确定因素, 然后用模糊综合评价确定评价结果。模糊分析方法是基于层次分析法的。它们相互集成, 具有很好的可靠性[4]。对模糊综合评价通常按以下步骤进行:

　　(1) 确定因素集 (2) 确定评判集 (3) 进行单因素评判得 (4) 构造综合评判矩阵

　　2 工程实例

　　2.1 工程概况

　　瑞祥大街黄花沟桥位于保定市瑞祥大街与河堤路交叉口北侧, 建于2014年, 根据委托方提供的资料, 该桥全长为37.8m, 桥梁跨径形式为2×5+1—20+2×5m钢筋混凝土组合拱结构, 上部拱圈厚度为0.5米, 跨径为20米。根据保定市城市防洪规划, 该桥防洪标准为50年一遇, 桥梁设计水位为18.12米。

　　2.2 桥梁安全性评价体系的建立

　　在桥梁的检测过程中, 桥梁安全评价涉及诸多因素, 不可能或不必要对所有因素进行科学的评价, 并结合桥梁安全风险因素集的实际工程因素进行综合评价。首先, 目标系统的分析, 确定了影响桥梁安全的几个因素, 然后找出各因素水平因素的影响下, 逐步形成层次结构。本文选取桥梁的上部结构、下部结构以及桥面系三个主要部分建立一级因素集, 其下属各部分建立二级因素集如下所示。

　　桥面系W12={桥面铺装, 伸缩缝, 人行道及护栏, 排水系统, 照明}

　　依据《城市桥梁养护技术规范》对Ⅱ~Ⅴ桥梁技术状况评定标准分为五种。A级完好状态 (BCI达到90-100) , B级良状态 (BCI达到80-89) , C级为合格状态 (BCI达到66-79) , D级为不合格状态 (BCI达到50-65) , E级为危险状态 (BCI小于50) , 对于处于不同等级的桥梁有相应处理应对措施。由此确定桥梁安全评定等级评判集v 1, v 2, v 3, v 4, v5的分值为90, 80, 70, 60, 50。

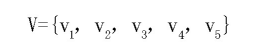
　　2.3 对桥梁检测结果进行综合评判

　　在桥梁安全性评价体系建立后, 一级元素1W, 对二级元素W11W12W13有着支配作用, 对于支配下的两两元素进行比较可以得出哪个风险更大, 同样需要用数字表达出来。根据相应的计算规则, 通过专家对各指标的相对重要性得分可以得出模糊判断矩阵, 模糊判断矩阵确定评价的质量直接相关, 所以我们应该选择的行业经验的专家有责任做出判断。

　　通过现场技术人员的专业检测之后, 根据真实的检测结果, 经过技术专家的专业综合评定可以得出各个层面对应的判断矩阵为:

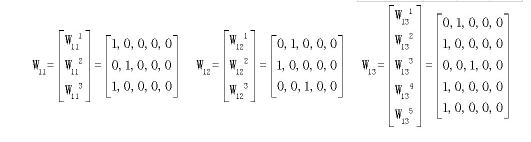
　　各个层面对应的排序权值为:

　　由以上数据可以得出该桥最终评判结果向量A={0.413, 0.533, 0.054, 0, 0}

　　2.4 得出评判结果

　　通过对该桥目前整体质量进行了调查, 检测发现桥面平整, 路面完好, 桥下拱顶存在微小裂缝, 拱圈钢筋保护层厚度良好, 不存在露筋现象。北侧护坡损坏严重, 南侧护坡保护完整。东北侧桥台存在一定程度的破坏, 其他侧桥台保护完好。总体外观情况良好, 满足规范使用要求。根据最大隶属度原则以及各个等级对应的分值可以得出该桥的安全度分值为83.59分, 从而确定该桥处于B级良好状态, 应进行日常保养和小修。

　　3 结语

　　这几年, 我国交通规划的完善以及运输业的快速发展, 将带动大量桥梁建设, 桥梁的安全问题逐渐成为桥梁行业焦点问题, 公路桥梁安全已成为影响民生, 国民经济发展的关键。桥梁检测是消除桥梁的安全问题避免安全事故发生的有效途径, 通过模糊数学在桥梁检测中的应用, 对桥梁检测的结果有了一个系统化的梳理, 通过结合模糊数学理论可以全面、精确、方便的得出桥梁安全度的综合评判, 准确的反映处桥梁当前所处的状态以及所面临的风险, 位桥梁在日后的运营加固提供了准确而有效的依据。

　　参考文献
　　[1] 张宝东, 庆虹桥检测评估的技术研究[D]辽宁工程技术大学, 2005。
　　[2]刘永振.数学方法[M].辽宁:辽宁人民出版社, 1987。
　　[3]李洪兴.工程模糊数学方法及其应用[M}.天津:天津科学技术出版, 1993.
　　[4] 王洪涛.模糊综合评判法在工程项目风险分析中的应用[D}.深圳:深圳大学建筑与土木工程学院, 2014.