工程流体力学主要研究在各种力的作用下,流体本身的静止状态和运动状态,以及流体和固体壁面、流体和流体间、流体与其他运动形态之间的相互作用和流动的规律。下面我们就为大家介绍几篇关于工程流体力学论文范文,供给大家参考。
工程流体力学论文范文第一篇:非牛顿流体下冶金熔池中气泡运动的研究进展
作者:赵凯 申耀宗 张兴华 魏志芳 王彬
作者单位:华北理工大学冶金与能源学院
摘要:对冶金反应器中气泡行为进行研究是提高冶金熔池反应效率、实现高效熔炼的重要途径。实际熔炼过程中的熔体是气、液、固三相流的非牛顿流体,非牛顿流体中的气泡运动和牛顿流体中的气泡运动相似,同样会经历气泡的产生、聚并以及破裂过程,但非牛顿流体以其自身复杂的流变性,使得气泡在非牛顿流体中的运动区别于牛顿流体中的运动特性和形态特性,并且由于气泡运动而造成对周围液相的影响也有所不同。目前关于非牛顿流体下气泡运动的研究都存在很多理想假设和很大的局限性,与实际工艺条件下的流体存在很大差距。本文对关于气泡行为的运动机理和气泡运动在非牛顿流体中的技术应用进行了阐述,介绍了当下的研究体系机理、现状以及未来研究的方向。
作者简介:赵凯(1981-),男,博士,副教授,研究方向为炼铁理论与工艺、余热回收。;
关键词:气泡运动;非牛顿流体;牛顿流体;运动机理;冶金熔池;技术应用;
Abstract:Research on bubble behavior in metallurgical reactors is an important way to improve the reaction efficiency of metallurgical baths and realize high-efficiency smelting. The melt in the actual smelting process is a nonNewtonian fluid of gas,liquid,and solid three-phase flow. The bubble motion in a non-Newtonian fluid is similar to the bubble motion in a Newtonian fluid,and it will also experience the bubble generation,coalescence and rupture process,but with its own complex rheology,Newtonian fluid makes the movement of bubbles in non-Newtonian fluids different from the movement characteristics and morphological characteristics of Newtonian fluids. The influence of bubble movement on the surrounding liquid phase is also different. The current research on bubble motion under non-Newtonian fluids has many ideal hypotheses and great limitations,which are far from reality. This article describes the motion mechanism of bubble behavior and the technical application of bubble motion in non-Newtonian fluids,and introduces the current research system mechanism,status quo and future research directions.
Keyword:bubble motion; non-Newtonian fluid; Newtonian fluid; movement mechanism; metallurgical molten pool; technology application;

在冶金领域中,熔池中的多相流熔炼主要分为牛顿流体和非牛顿流体,当前研究对于简化后的牛顿流体居多,而在实际生产中,熔池的熔炼并非理想状态,由于煤粉、渣等存在于熔炼过程中,流体往往呈现出非牛顿流体状态。目前,针对于气泡运动的研究主要有数值模拟以及实验分析的方法[1,2,3,4],气泡相关特性的应用被广泛运用于石油、环境以及化工等领域[5,6,7,8,9,10].本文通过对比在不同条件下牛顿流体和非牛顿流体熔炼中气泡的运动规律,结合自身课题中侧吹熔池熔炼中的研究现状,对气泡运动在相关流体中的变化和机理进行了分析,提出了气泡运动在未来的发展方向。
1 气泡行为的运动机理
对于反应器中的多相流行为,气泡尺寸以及形状的变化是一个关键参数,由于气泡和气泡之间的相互作用以及气泡和周围环境的相互作用,不同气泡的尺寸和形状使得不同的运动阶段会呈现出不同的影响效果。
1.1 牛顿流体中的气泡行为
气泡在产生后,会出现聚合与破裂行为,其过程也十分复杂。对于气泡的聚合,在目前没有统一的表达式来描述,通常要根据自身的实验条件来进行拟定;对于气泡的破裂,目前的认知主要是认为气泡在运动的过程中,由于液相作用促发湍流漩涡,引发碰撞,以此获得变形能量,发生破碎[11].
目前,对于气泡运动路径的研究,大多学者都会采用高速摄像机的方法进行采集,而对于气泡周围速度场的研究,PIV的方法显得更为普遍[12].其中,闫红杰[13]等对静止水中的单气泡行为进行了研究,气泡在液体中运动时,主要受重力、惯性力以及浮力和表面张力的作用,因此采用了不同的准则数进行描述,由此得到We和Re的预测效果最优,除此之外,还发现气泡在静止液体上升的过程中,气泡的运动路径会随着气泡的不断变形而呈现出不同的运动轨迹。气泡的形状变化还会受到周围条件的制约,从各项研究结果可以了解,流动环境对小气泡的影响程度远大于流动环境对大气泡的影响,且随着气泡尺寸的逐步增大,流动的依赖性会逐渐减小,关于这一点,Ziegenhein T等[14]运用了PIV技术在不同流动条件下的鼓泡塔实验研究中也有所论述。
对于牛顿流体来说,在不同的流体体系中,气泡的生长机理可以简要概括为气泡之间的上浮碰撞、湍流随机碰撞以及湍流剪切碰撞,在大部分的浸入式气泡中,都会经历气泡的聚合和破裂。徐玲君等[15]通过采用基于流体体积法下的几何重构技术以及相关的处理程序对单个气泡在静水中的特性进行研究,得知气泡的变形在不同的气泡大小状态下是不一样的,气泡越小,其内外压差越大,此时更容易维持球形,而气泡越大,内外压差反而会减小,此时会在气泡两侧以及尾部形成尾迹流,进而产生推力,促使气泡发生形变。
对于气泡上升和聚并的过程,王乐等[16]以及邢少鹏等[17]都通过数值模拟的方法对多气泡的运动进行了研究,一方面,发现气泡间距的变化会直接影响气泡相互融合的结果,除此之外,不同直径和不同位置的切换也是影响气泡聚并行为的重要因素;另一方面,研究表明气泡直径以及运动速度的增加会加剧尾随气泡的上升。
1.2 非牛顿流体气泡行为
非牛顿流体中的气泡行为同样会经历生成、上升以及破裂过程,由于非牛顿流体中存在较为复杂的流变性,导致气泡的聚并、碰撞所表现出来的一些相关特性异于牛顿流体。
在气泡的生成过程中,Acharya等[18]通过高速摄像机对有机玻璃管中的流体进行观测,发现在黏弹性溶液气泡形成过程中,聚合物溶液的弹性会对气泡造成一定的影响,表现在气泡聚并速率小、聚合次数多。Miyahara等[19]研究了非牛顿流体中浸没孔口的气泡形成,建立了两阶段气泡生成模型,用以预测气泡体积。该模型考虑了非牛顿流体中的流变参数等影响,分析结果认为在流变参数大的情况下,气泡会趋向于非球形变化,惯性力是影响气泡形成的主导因素,导致在非牛顿流体中气泡所形成的体积会比牛顿流体中所形成的大。关于这一结论,Costes等[20]在关于非牛顿流体的气泡形成中也有同样的论述。除此之外,Favelukis等[21]针对非牛顿流体中的气泡生长建立了动力学模型,通过研究发现,随时间的变化,气泡半径的变化呈现指数函数趋势,并且在气泡形成的后期,气泡形态的变化是区别于前期的,主要受传质控制。
非牛顿流体中气泡聚并过程的基本运动机理和牛顿流体相似,首先尾随气泡需要到达前行气泡的尾流区,由于力的作用促使气泡发生碰撞,从而发生聚并。Shiloh等[22]通过对稀分散体中的气泡聚并行为进行研究,把气泡的聚并效率和碰撞速率相联系,得出了液滴尺寸和聚并速率两者与滞留率的基本关系,并表明流体的黏性会影响气泡的聚并速率;碰撞和聚并行为并非先后伴随发生。Crabtree等[23]通过高速摄像机对黏性流体中气泡的聚并行为进行研究,并建立关联模型,发现尾迹流可以较好地描述气泡的聚并现象,分析原因是由于气泡浮力以及惯性阻力的共同作用所控制。LI H Z等[24]采用粒子图像测速和双折射测量技术对非牛顿流体中的气泡相互作用及聚并行为进行了研究,提出气泡所产生的应力以及松弛形成的动力竞争控制了气泡之间的相互作用,对于线性气泡的研究提供了较好的指导。
在气泡的破裂过程中,非牛顿流体下的球形气泡发生破裂对气泡周围的流体产生拉伸作用,而这种拉伸行为对工业研究有着重要作用[25].针对于非牛顿流体中的气泡破裂行为,Tanasawa等[26]通过建立三参数线性模型对黏弹性液体中的气泡破裂行为进行了研究,发现在同时具备黏性和弹性的条件下,其液体对气泡破裂所产生的黏性阻力要小,并且在气泡的破裂过程中,气泡伴随着发生一定的摆动。Yoo等[27]选用了相关数学模型,采用有限差分法对其进行求解,对黏性液体的气泡行为进行了研究,指出气泡在快速扩散下会发生摆动行为,但这一行为的产生是有前提条件的,在极低的扩散情况下,同样存在气泡的摆动,但此时这一现象与流变性质无关,气泡摆动行为都是伴随着气泡的破裂而产生的。
对比牛顿流体和非牛顿流体下的气泡特性机理,可以得知非牛顿流体在相关的气泡机理上和牛顿流体下的气泡机理相似,气泡都会经历生成、聚并以及破裂的过程,且在气泡上升到破裂的整个过程里,同样会受到与气泡本身相关的力的作用,但是面对同样的过程,非牛顿流体下的气泡行为会呈现出不同的形态特性以及运动特性。
2 非牛顿流体中的技术应用
非牛顿流体中的气泡行为具有和牛顿流体中气泡行为不同的特性,关于非牛顿流体下的气泡运动对周围流场的影响以及气泡之间相互作用的认知,对于实际熔炼效率的提高和能耗的控制都具有重要意义。目前对非牛顿流体中的多相流探索主要是在射流特性研究以及非牛顿流体下的喷嘴特性影响研究等方面[28,29,30,31],而在冶金领域中,则主要集中于冶金渣的相关研究中。
2.1 非牛顿流体在冶金渣中的应用
冶金领域内的泡沫渣问题在近年来越来越被重视,太强的泡沫渣会引起过量的喷溅,而适量的泡沫渣则有利于反应的进行。
吴铿等[32,33]针对泡沫对冶金过程中熔渣的影响进行了研究,通过对熔渣的一维本构方程进行分析,提出了一种判断泡沫化程度的方法,同时,也对非牛顿流体下的熔渣流变特性进行了相关研究,探究了温度变化以及添加剂的加入对流变特性的影响,通过研究发现:针对不同粒度条件下的添加剂,泡沫所呈现出来的流变特性是不一样的,且非牛顿流体的流变特性在粒度小的添加剂中更为显著。该研究不足之处就在于所采用的测量熔体流变曲线的方法是一种相对的测量方法,存在一定的误差,虽在后期对所得本构方程进行了对比性的误差分析,但此方法还存在理想因素考虑偏多的问题。
关于非牛顿流体下的冶金熔渣和泡沫化的关系,Y.Ogawa等[34]对减渣冶炼中的气泡行为以及相关碳质材料的控制进行了研究,采用了X射线透视法,观察熔融还原炉实验,发现提高含碳材料的加入量可以较为有效地减小炉渣的起泡率,增大气泡的接触面积和频率也有类似的效果,除此之外,也发现大颗粒碳质材料因本身尺寸较大且含有活性孔隙,对气泡的排出有利。该研究的不足之处就在于实验做了很多理想化的假设,使得结果存在一定的局限性。针对于此,白晨光等[35]对非牛顿流体条件下熔渣流变特性的研究情况进行了说明,提出了在熔渣体系中,产生泡沫化的原因和本身所具有的非牛顿流体特性是密不可分的,且不同大小粒度的材料作为添加剂所造成的熔渣流变特性也不同。
在其他方面,Y.Zhang等[36]采用X射线观察法研究了含碳颗粒物和泡沫之间的相互作用,发现在颗粒物的总表面积和液态渣表面积之比逐步增大的过程中,泡沫指数会出现明显的降低,并指出焦炭对液态渣具有消泡作用。岳宏瑞等[37]以高炉渣为基础,研究含钛熔渣的非牛顿流体现象,指出在加入不同质量分数的Ti C时,熔渣所表现出来的触变特性也是不同的。具体来讲,Ti C含量的增加以及温度的降低都会使这种特性更为显著,而针对含Ti C的熔渣,吴铿等[38]对碳还原Ti O2所导致的发泡过程进行了研究,通过对当前发泡特性方程的改进,进行了相关实验,提出了发泡系数和消泡系数可以对发泡程度进行定量的描述,而针对整个过程的发泡情况,也可用发泡强度和发泡寿命进行定量描述,不足之处在于该项研究仅仅实现了定量分析的突破,在实际研究中还存在一定的局限性。
非牛顿流体下的冶金渣是未来冶金行业的重要课题,而对于其中的气泡行为,现阶段的研究都进行了大量的简化假设,未来还需要对实验机理进一步把控,对实验过程实现进一步完善,从而实现从理想研究到实际应用的过渡。
2.2 非牛顿流体中射流、喷嘴特性研究
无论是在熔池熔炼领域还是其他反应器内反应机理研究领域,射流特性以及喷嘴特性都是影响反应效率、发现相关机理的重要途经。
Miyahara等[39]对浸没孔口下的气泡形成进行了研究,所用液体为甘油水、乙醇水等溶液,主要对单气泡行为进行了实验,从而得出了不同种类的流型,但是由于当时技术限制并没有对大孔径下同时产生的气泡形成以及漏液现象进行实验验证。Dekee等[40]对非牛顿流体条件下的气泡运动进行了实验研究,通过对两个喷嘴所产生的气泡进行观察,发现尾流气泡是在进入先前气泡的尾迹后,再加速完成碰撞,并绘制了初始孔口分离距离和气泡聚集形成的体积之间的函数关系图,不足之处在于,在气泡注入的同时,黏性流体会存在轻微的干扰作用。Davidson等[41]通过摄影观测对水平喷孔下的气泡形成进行研究,研究对象为矿物油和水,应用相关数学模型理论,发现在低流量下,孔口气泡形态通常为单"静态"气泡,此时气泡体积仅和孔口半径和表面张力有关,与流量无关;在高流量下,随着气泡频率的增大,气泡体积变为和流速相关,而与表面张力无关。杨辉等[42]研究了双喷嘴下的非牛顿流体中的气泡运动,通过VOF-CSF法模拟双喷嘴下的气泡形成以及碰撞过程,发现了3种不同的流型,流型的形成受周围环境的影响,且在周围液相环境的影响下,两个喷嘴所产生的气泡的聚并也有所区别,但是该实验所研究的液相仅局限于不可压缩流体,存在一定的局限性。
关于非牛顿流体中的射流研究,王玉龙等[43]通过搭建高速摄影光学研究平台,对幂律流体下的射流现象进行了研究,发现在幂律流体中,因为高黏度剪切变稀的物性,降低了射流的轴转换振荡现象,但随着射流的进行,这种现象还会受到射流速度的影响。曹伟等[44]同样对幂律流体下的射流进行了研究,对于雾化速度场,运用了PIV技术,发现了幂律流体的雾化效果之所以会被气流的扰动所影响,主要是通过影响液膜表面波强度,从而使液膜出现破裂,造成液膜宽度减小,最终影响雾化。而关于非牛顿流体中的雾化应用,蒋丽莎等[45]对其射流特性进行了相关研究,指出牛顿流体雾化张角要大于黏弹性流体,且喷射雾滴的粒径会随距离的增大而增大。幂律流体研究的不足之处就在于其进行了大量的简化假设,和实际应用还存在一定的差距。
2.3 气泡运动研究的局限性及未来发展方向
目前关于气泡运动的研究仅局限于牛顿流体下的气液两相流研究,大多研究首先通过数值模拟的方法探究牛顿流体下的熔池喷溅现象以及速度场和流场情况,其次通过物理模拟的方法对理想条件下的模拟结果进行了水模型实验验证,而对于熔池中的研究都忽略了实际熔炼工况下存在的固态炉料。在实际熔炼过程中,熔池中的流体并非是理想条件下的牛顿流体,而是包含气、液、固三相流的非牛顿流体,基于此,在未来关于侧吹熔池熔炼炉的课题研究中,需要在原先牛顿流体下的熔池气泡运动的研究基础上做出相关改进。当流体作为非牛顿流体形式存在时,进一步探究熔池中喷吹气泡在流变特性的作用下,对周围流场、速度场以及产生的搅动喷溅效果的相关现象变化,从而实现理论分析和实际应用的结合。
3 结语
气泡运动的研究在工程领域内有着较大的作用,而对冶金反应器中气泡行为的研究又是提高冶金熔池反应效率、实现高效熔炼的一个至关重要的环节。近年来针对于气泡行为的研究大多停留在牛顿流体中,而对非牛顿流体下的气泡运动研究并不多。但对于冶金领域来说,由于在实际的熔炼过程中往往伴随着冶金渣、煤粉的存在,大部分的实际熔炼往往呈现的是非牛顿流体特性。而非牛顿流体中的气泡运动和牛顿流体中的气泡运动是相似的,同样会经历气泡的产生、聚并以及破裂过程,但非牛顿流体以其自身复杂的流变性,使得气泡在非牛顿流体中的运动区别于牛顿流体中的运动特性、形态特性以及由于气泡运动对周围液相产生的影响,从而导致实际运行过程不同。结合当下对非牛顿流体的了解,未来还需对非牛顿流体下的气泡行为特性进一步研究,特别是对当前非牛顿流体研究中存在的简化假设太过理想、气泡运动研究单一以及相关理论机理分析不全面等不足之处,需要加强突破研究。
参考文献
[1] WU Liangyu,LIU Lingbo,HAN Xiaotian,et al. Numerical simulation on dynamic behaviors of bubbles flowing through bifurcate Tjunctionin microfluidic device[J]. Chinese Physics B ,2019,28(10):421-431.
[2] KURIAN J Vachaparambil, KRISTIAN Etienne Einarsrud. Numerical simulation of bubble growth in a supersaturated solution[J]. AppliedMathematical Modelling,2020,81:690-710.
[3] LIM Do Yeong BANG In Cheol. Controlled bubble departure diameter on biphilic surfaces for enhanced pool boiling heat transfer perfo
rmance[J]. International Journal of Heat and Mass Transfer,2020,150.
[4] POULAIN S,VILLERMAUX E,BOUROUIBA L. Ageing and burst of surface bubbles[J]. J. Fluid Mech,2018:636-671.
[5]赵立华,郭建龙,徐佳亮,等。RH真空室内气泡行为的研究[J].工程科学学报,2018,40(4):453-460.
[6]LI Y J,LIU M Y,LI X N. Single bubble behavior in gas -liquidsolid mini-fluidized beds[J]. Chemical Engineering Journal,2016 ,286:497-50
[7] HUBER M,DOBESCH D,KUNZ P,et al. Influence of orifice type and wetting properties on bubble formation at bubble column reactors
[J]. Chemical Engineering Science,2016, 152:151-162.
[8] TSUGE Hideki,TEZUKA Yusuke,MITSUDANI Masae. Bubble formation mechanism from downward nozzle- effect of nozzle shape andoperating parameters[J]. Chemic al Engineering Science ,2006(61):3290-3298.
[9] TRIPATHI M K ,SAHU K C,KARAPETSAS G,et al. Bubble rise dynamics in a viscoplastic material[J]. Journal of Non-Newtonian Fluid Mechanics,2015,222:217-226.
[10]LI X N,LIU M Y,MAY L,et al. Experiments and meso-scale modeling of phase holdups and bubble behavior in gas-liquidsolid mini-fluidized beds[J]. Chemical Engineering Science,2018, 192:725-738.
[11]邵品冶金熔体内气泡行为的数值模拟研究[D].沈阳东北大学, 2015:73-98.
[12] DIETRICH N,MAYOUFI N,PONCIN S,et al. Bubble formation at an orifice:a multiscale investigation[J]. Chemical Engineering Science,2013,92(14):118-125.
[13]闫红杰,赵国建,刘柳,等静止水中单气泡形状及上升规律的实验研究[J]中南大学学报(自然科学版) , 2016,47(7):2513-2520.
[14] ZIEGENHEIN T,LUCAS D. Observations on bubble shapes in bubble columns under different flow conditions[J]. Experimental ThermaI and Fluid Science ,2017,85:248-256.
[15]徐玲君,陈刚,邵建斌,等单个气泡静水中上升特性的数值模拟[J].沈阳农业大学学报, 2012,43(3):357-361.
[16]王乐,曹洲榕,郑西朋,等三气泡上升聚并的数值模拟研究[]/2016全国水环境污染控制与生态修复技术高级研讨会论文集。2016:168-174.
[17]邢少鹏,黄亚宇多个气泡的动态模拟分析[J]新技术新工艺, 2017(3):39-42.
[18] ACHARYA A,ULBRECHT J. Note on the influence of viscoelasticity on the coalescence rate of bubbles and drops[J] AIChE Journal,1978,24(2):348-351.
[19] MIYAHARA T,WANG W H,TAKAHASHI T. Bubble formation at a submerged orifice in non-Newtonian and highly viscous Newtonian liquids[J]. Chemical Engineering of Japan, 1988,21(6):620-626.
[20] COSTES J,ALRAN C. The formation of bubbles in a non-Newtonian liquid[J]. The Chemical Engineer,1978,330(1):191-193.
[21] FAVELUKIS M,ALBALAK R J. Bubble growth in viscous Newtonian and non-Newtonian liquids[J]. Chemical Engineering of Japan, 1996,63(3):149-155.
[22] SHILOH K S,SIDEMAN S,RESNICK W. Coalescence and break-up in dilute polydispersions[J]. The Canadian Journal of Chemical Engineering, 1973,51(5):542-549.
[23] CRABTREE J R,BRIDGWATER J. Bubble coalescence in viscous fluids[J]. Chemical Engineering Science, 1971,26(6):839-851.
[24]LI H Z,FRANK X,FUNFSCHILLING D,et al. Towards the understanding of bubble interactions and coalescence in non-Newtonian fluids:A cognitive approach[J]. Chemical Engineering Science,2001 , 56(21/22):6419-6425.
[25]范文元,朱春英,马友光,等。非牛顿流体中的气泡行为[J].化学工业与工程, 2006(5):446-452.
[26] TANASAWA I,YANG W J. Dynamic behavior of a gas bubble in viscoelastic liquids[J]. Journal Applied Physics, 1970,41(11):4526-453
[27] Y0O H J,HAN C D. Oscillatory behavior of a gas bubble growing(or collapsing)in viscoelastic liquids[J] AIChE Journal, 1982,28(6):1002-1009.
[28] CHOO Y J,KANG B S. A study on the velocity characteristics of the liquid elements produced by two impinging jets[J]. Experiments inFluids ,2003,34(6):655-661.
[29] BAI F,DIAO H,ZHANG M,et al. Breakup characteristics of power-law liquid sheets formed by two impinging jets[J]. Fluid Dynamics Research,2014. ,46(5):6-21.
[30] LIU Mingyan,HU Zongding. Studies on the hydrodynamics of chaotic bubbling in a gas liquid bubble column with a single nozzle[J]. Chemical Engineering Science ,2004,27(5):537-547.
[31] MA Dou,LIU Mingyan,ZU Yonggui,et al. Two-dimensional volume of fluid simulation studies on single bubble formation and dynamicsin bubble columns[J]. Chemical Engineering Science ,2012,72:61-77.
[32]吴铿,储少军,潜伟。冶金渣非牛顿流变特性对其泡沫化的影响[J].化工冶金, 1999(2):199-204.
[33]吴铿,储少军,潜伟。非牛顿流体冶金熔渣的流变特性[J]钢铁,1998(11):16-20.
[34] OGAWAY. Slag Foaming in Smelting Reduction and its control with carbonaceous materials[J]. ISIJ International,1992,32(1):87-94.
[35]毛红霞,白晨光,邱贵宝,等。非牛 顿冶金熔渣流变特性的研究进展[J]重庆大学学报(自然科学版) , 2005(6):52-56.
[36] ZHANG Y,FRUEHAN R J. Effect of carbonaceous particles on slag foaming[J]. Metallurgical Materials Transactions, 1995,26B(8):813-819.
[37]岳宏瑞,姜涛,薛向欣。含钛冶金熔渣非牛顿流体现象的表征与分析[J]中国有色金属学报, 2017,27(7):1485- 1492.
[38]吴铿,赵勇,潜伟,等。合成高炉渣中Ti O2还原的发泡特性参数[J].中国有色金属学报, 2001,12(4):817.
[39] MIYAHARA T,IWATA M,TAKAHASHI T. Bubble formation pattern with weeping at a submerged orifice[J]. Chemical Engineering Japan,1984,17(6):592-597.
[40] DEKEE D,CARREAU P J,MORDARAKI J. Bubble velocity and coalescence in viscoelastic liquids[J]. Chemical Engineering Science, 1986, 41(9):2273-2283.
[41] DABIDSON L,AMIC E. Formation of gas bubbles at horizontal orifices[J]. AIChE Journal, 1956,2(3):337-342.
[42]杨辉,朱春英 ,马友光,等。非牛顿流体中双喷嘴连续气泡的生成与聚并[J]化学工程,2016 ,44(8):37-41.
[43]王玉龙,尹燕,白富强,等幂律流体椭圆形射流破碎的试验研究[J].燃烧科学与技术, 2019,25(2):161-168.
[44]曹伟幂律流体双股射流碰撞雾化的试验研究[D].哈尔滨哈尔滨工业大学, 2016:54-69.
[45]蒋丽莎非牛顿流体雾化射流性能测试及喷嘴结构优化设计[D].杭州:中国计量大学, 2018.
文献来源:赵凯,申耀宗,张兴华,魏志芳,王彬。非牛顿流体下冶金熔池中气泡运动的研究进展[J].中国有色冶金,2021,50(02):1-6.
工程流体力学论文范文第二篇:流体运动估计光流算法研究综述
作者:邵绪强 杨艳 刘艺林
作者单位:华北电力大学控制与计算机工程学院
摘要:对流体图像序列进行运动分析一直是流体力学、医学和计算机视觉等领域的重要研究课题。从图像对中提取的密集精确的速度矢量场能够为许多领域提供有价值的信息,基于光流法的流体运动估计技术因其独特的优势成为一个有前途的方向。光流法可以获得具有较高分辨率的密集速度矢量场,在小尺度精细结构的测量上有所改进,弥补了基于相关分析法的粒子图像测速技术的不足。此外,光流方法还可以方便的引入各种物理约束,获得较为符合流体运动特性的运动估计结果。为了全面反映基于光流法的流体运动估计算法的研究进展,本文在广泛调研相关文献的基础上,对国内外具有代表性的论文进行了系统阐述。首先介绍了光流法的基本原理,然后将现有算法按照要解决的突出问题进行分类:结合流体力学知识的能量最小化函数,提高对光照变化的鲁棒性,大位移估计和消除异常值。对每类方法,从问题解决过程的角度予以介绍,分析了各类突出问题中现有算法的特点和局限性。最后,总结分析了流体运动估计技术当前面临的问题和挑战,并对未来基于光流法的运动估计算法的研究方向和研究重点进行了展望。
关键词:流体运动估计;光流法;流体力学;光照变化;大位移估计;异常值检测;
作者简介:邵绪强,1982年生,男,副教授,主要研究方向为计算机图形学、虚拟现实。E-mail:shaoxuqiang@163.com;*杨艳,通信作者,女,硕士研究生,主要研究方向为计算机图形学、流体运动估计。E-mail:2385439823@qq.com;刘艺林,男,硕士研究生,主要研究方向为计算机图形学、流体可视化。E-mail:610852885@qq.com;
Abstract:The motion analysis of fluid image sequences has been an important research topic in the fields of fluid mechanics, medicine, and computer vision. The dense and accurate velocity vector field extracted from image pairs can provide valuable information for these fields. For example, in the field of fluid mechanics, the velocity vector field can be used to calculate the divergence and curl fields of fluid; in the field of meteorology, the analysis of the velocity vector field can be used to provide weather forecast; in the field of medicine, the velocity vector field is applied to match medical images. In recent years, fluid motion estimation technology based on an optical flow method has become a promising direction in this subject due to its unique advantages. Compared with particle image velocimetry based on a correlation method, an optical flow method can obtain a denser velocity field and can estimate the motion of a scalar image and not just a particle image.In addition, an optical flow method can easily introduce various physical constraints in accordance with the motion characteristics of the fluid and obtain more accurate motion estimation results. In accordance with the basic principles of an optical flow method, this paper reviews a fluid motion estimation algorithm based on an optical flow method. Referring to a large number of domestic and foreign studies, existing algorithms are classified in accordance with outstanding problems to be solved: combining the energy minimization function with the knowledge of fluid mechanics, improving robustness to illumination changes, estimating large displacements, and eliminating outliers. Combining the minimization function with the knowledge of fluid mechanics introduces various physical constraints for improving the energy minimization function, providing physically meaningful data items and regularization terms, and improving the accuracy of fluid motion estimation results.Algorithms for improving robustness to illumination changes can be classified into four types: using a high-order constancy assumption to expand data items that depend on the constant brightness assumption, extracting illumination-invariant features in the image for data items, using structure-texture decomposition methods, and establishing a mathematical model for light changes. Various methods are applicable to different light change conditions. For the large displacement estimation problem, the pyramid-based multi-resolution optical flow method is first used; however, this method cannot estimate the large displacement of fine structures. To solve this problem, a hybrid motion estimation method that combines the cross-correlation method with a wavelet-based optical flow method is proposed in recent research. This hybrid method uses the crosscorrelation method to calculate the large displacement of a fine structure and then uses an optical flow method to refine and redetermine the flow field, combining the advantages of the two methods. The optical flow estimation method based on wavelet transform provides a good mathematical framework for the multi-resolution estimation algorithm and avoids the linear problem that exists in the "coarse-to-fine" multi-resolution framework when estimating large displacements. Methods for eliminating outliers can be divided into three basic categories: methods that use a robust penalty function, median filtering,and forward-backward optical flow consistency check. In this paper, each kind of method is introduced from the perspective of the problem solving process, and the characteristics and limitations of existing algorithms are analyzed in various outstanding problems. Finally, the major research problems are summarized and discussed, and several possible research directions for the future are proposed. First, an optical flow method introduces various physical constraints into the objective function to conform to fluid motion characteristics. Hence, although accurate estimation results can be obtained, the resulting optical flow equation is too complex to solve, and no good numerical solution is obtained. Second, several methods based on an optical flow method exhibit different advantages under varying light change conditions; they also have corresponding shortcomings. Therefore, further research on how to combine the advantages of various methods to cope with different light changing conditions is particularly important. Third, although the hybrid method that combines the cross-correlation and optical flow methods can utilize the advantages of the two methods to obtain high-resolution motion results for the large displacement problem, this method can only be successfully applied to the motion estimation of particle images at present. Thus, exploring this method for other types of fluid motion images is worthwhile. Finally, an optical flow method requires complex variational optimization and its computational efficiency is low. Although some graphics processing unit(GPU) parallel algorithms proposed in recent years have effectively improved computational efficiency, they still cannot achieve real-time estimation. Therefore, improving the computational efficiency of fluid motion estimation algorithms and realizing real-time estimation are among the directions that are worth studying in the future.
Keyword:fluid motion estimation; optical flow method; fluid mechanics; illumination change; large displacement estimation; outlier detection;

0 引言
流体运动估计技术在日常生活的众多领域发挥着重要作用,对从流体图像序列中提取的速度场进行分析,有助于更深入地了解复杂的流体运动并提取有用的信息。
粒子图像测速(particle image velocimetry,PIV)(Adrian,1991)是一种广泛使用的流体运动估计技术。其基于两个连续粒子图像之间局部空间相关性,通过搜索图像对的两个查询窗口之间互相关的最大值,获得查询窗口之间的位移矢量。这种依赖于互相关函数的PIV技术虽然能够简单有效地从图像序列间获取速度矢量场,但仍存在许多不足。首先,其假设查询窗口内的位移矢量保持一致,这使得获取的速度场空间分辨率低,无法测量流场中的小尺度精细结构。其次,PIV技术主要用于粒子图像,无法可靠获取标量图像的速度矢量场。最后,PIV技术缺乏物理解释,对图像序列进行运动估计时,平等地对待各种性质的运动物体。
研究发现光流法非常适合流体运动估计(Liu等,2015)。与基于互相关的PIV技术相比,光流法可以获取更加密集的速度场,而且可以对标量图像进行运动估计而不仅限于粒子图像。此外,与PIV技术相比,光流法更能适应各种物理约束。基于光流法的流体运动技术是对PIV技术的良好补充。
虽然现有的基于光流法的流体运动估计技术已经广泛用于各种流体测速场景,但仍存在计算耗时、鲁棒性不足等问题。本文从光流法的基本原理入手,根据光流法需要解决的几个关键问题对现有的算法进行分类,并对每一类方法从问题解决的角度予以介绍。
1 光流法的基本原理
光流本质上是3维场景的物体运动投影到2维图像平面表现的像素点亮度变化。光流计算即从图像数据中估计物体的运动。Horn和Schunck(1981)开创性地提出了经典的变分光流估计模型,该模型的目标函数是包含一个数据项和一个平滑项的能量函数的最小化。数据项主要基于亮度守恒假设,即同一个像素点的亮度(灰度值)在相邻两帧图像内保持不变,即
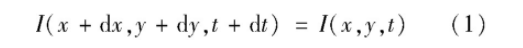
式中,I(x,y,t)表示t时刻坐标为(x,y)的像素点的亮度(灰度值)。对式(1)左边进行泰勒展开并整理可得
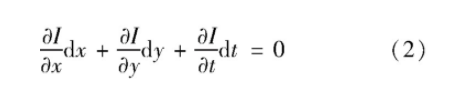
假设坐标为(x,y)处的像素点的速度为w(x,y)=(u,v)T.将速度的定义公式代入式(2),可得
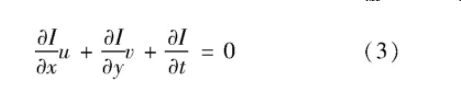
单独使用式(3)估算速度的两个未知分量,即u和v,不能获得唯一解,这称为光流计算的孔径问题(aperture problem),如图1 (Heitz等,2010)所示。为解决该问题,通常采用附加的平滑项Eregu(u,v),执行流场的空间平滑度一致性,具体为
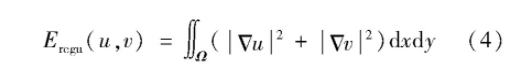
式中,Δ表示梯度算子。结合式(3)和式(4)可以获得经典变分光流法的能量最小化函数E(u,v),具体为
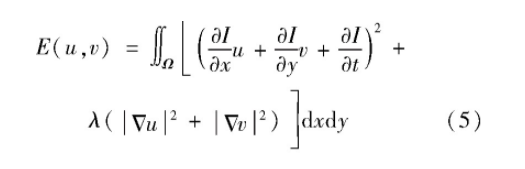
式中,λ是参数,用于调节平滑项所占的比重。
图1"孔径"问题示意图(Heitz等,2010)
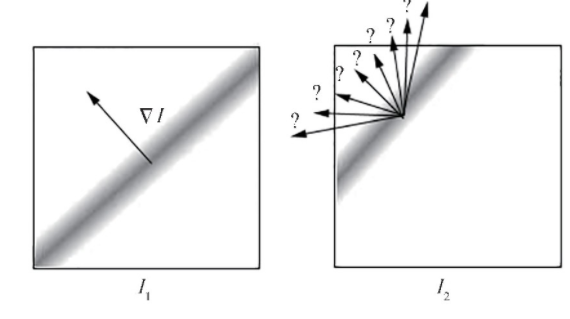
Fig.1 Schematic illustration of the aperture problem(Heitz et al.,2010)
光流法最初是在计算机视觉领域提出的,主要用于从图像序列中估计明显的刚性运动,由于其能够从图像对中获取密集的速度矢量场,成为实验流体力学、医学和气象学等领域的研究热点,广泛用于各种流体运动场景。
2 基于光流法的流体运动估计技术
自经典光流模型提出以来,不断进行研究和改进,以提升算法的精度、鲁棒性和时空分辨率等性能,更好地对流体图像序列进行运动估计。本文按照光流法需要解决的几个关键问题,将现有算法分为结合流体力学知识的能量最小化函数、提高对光照变化的鲁棒性、大位移估计和消除异常值等4类方法。
2.1 结合流体力学知识的能量最小化函数
Wildes等人(2000)和Corpetti等人(2002)尝试将经典光流模型应用于云运动估计,但是结果表明该模型不能准确地估计云的运动。经典的光流模型主要适用于估计各种自然场景中的刚性运动,其依赖的亮度约束方程不是通过任何物理原理推导而来,缺乏物理解释,难以捕获具有复杂运动模式的流体运动。为了克服该模型对流体图像序列的局限性,对其进行了改进和扩展。
通过引入基于质量和动量守恒定理推导的连续性方程,设计了一种专用于捕获流体运动的光流模型(Corpetti等,2000,2002,2003,2006),采用连续性方程作为数据项,并利用二阶散度-旋度(div-curl)正则化替换经典模型中的一阶正则化。基于物理的流动连续性方程能够将图像数据与流体流动行为联系起来。一阶正则化用作平滑项会因过度平滑而导致估计的矢量场具有低散度和旋度,而二阶div-curl正则化能够有效恢复流体运动的散度和旋度结构,更适用于复杂的流体运动估计。但是由于涉及高阶微分,该算法实现起来比较困难,而且较高的阶数还会导致计算成本增加。为解决该问题,在正则化项中添加了两个辅助变量ξ和ζ,作为真实散度和旋度的近似值,以减少模型的高阶行为。Liu和Shen(2008)根据3维物体空间中的传输方程或连续性方程在2维图像平面上的投影,推导出针对各种流体可视化的投影运动方程。并将此投影运动方程作为光流约束,进一步给出了基于物理的光流方程,正式建立了光流与流体流动之间的数学联系。需要指出,Corpetti等人(2002)使用的div-curl正则化不是基于流体力学原理推导出来的;Liu等人(2008)采用投影到2维图像平面上的navier-stokes方程为光流计算提供了基于物理的约束,得到的非线性约束非常复杂。Yang和Johnson(2017)利用Liu等人(2008)得到的基于物理的光流方程,提出一种散度补偿光流法,并成功应用于X射线图像的流场估计。
上述方法求解的速度场都是基于像素尺度的,对于刚体和简单流体运动而言,在该尺度下求解造成的信息缺失可以忽略不计。但是对于复杂的流体运动如湍流,其中存在的亚像素小尺度涡结构无法在像素点上得以体现。Cassisa等人(2011)和Zille等人(2014)引入大涡模拟的相关概念,提出一种亚网格传输方程模型(sub-grid transport equation),在亚像素尺度上考虑了湍流的小尺度速度分量,相比之前的光流模型,能够精确估计复杂的湍流运动,但是亚网格传输方程涉及的湍流扩散系数是根据经验选取的。Chen等人(2015)在此基础上,应用物理空间亚网格模型系统地计算嵌入光流约束方程中的小尺度扩散项,得到了改善的估计结果。
从以上研究可知,将湍流模型与变分光流模型结合起来估计复杂的湍流运动是很有前景的研究方向,但是这些方法都高度依赖一个用于在数据模型中对选取的湍流模型进行加权的正则化参数,该参数没有直接的物理解释且在实际应用中很难确定。Cai等人(2018)为采用不同策略的湍流运动估计,推导了一种新颖的基于位置不确定性的光流方程。首先根据Mémin(2014)的推导,将流体运动的欧拉速度分解为一个大尺度分量和一个称为位置不确定性的小尺度湍流分量。然后结合雷诺兹运输定理的随机表达式得出随机光流约束方程,该方程包含了小尺度分量的影响,涉及的参数都可以进行明确的估计而无需进行烦琐的调参。
对流体速度场进行分解有助于理解复杂的流体运动。Kohlberger等人(2003)基于亥姆霍兹分解定理提供了一种对图像序列中的非刚性结构进行稠密运动估计的方法,将速度场分为一个无散度分量和一个无旋度分量之和,使用速度势和流函数对这两个分量进行明确表示,并将该表示应用于亮度恒定约束方程(brightness constancy constraint equation,BCCE)和二阶正则化项。该方法可以直接估计速度势和流函数,利用这两个函数可以获得速度场的更多信息。首先,计算它们的梯度,得到无散度分量和无旋度分量。其次,对它们进行拉普拉斯运算,获得速度场的涡度和散度。最后,它们的极值提供了感兴趣的奇异点的位置,例如源、汇和漩涡。
利用Kohlberger等人(2003)提出的方法估计密集运动矢量,其解属于高维空间,但在跟踪等应用中需要提供低维解。为了获得低维解,提出了一种基于矢量场的亥姆霍兹分解的低维流体运动估计方法(Cuzol和Mémin,2005;Cuzol等,2007)。在该方法中,无散度分量和无旋度分量采用离散化的涡度和散度图通过正则化狄拉克测度进行近似,同时采用引入连续性方程的数据项和二阶div-curl正则化的平滑项。该方法在考虑较少数量的粒子时,可以实现更高的精度和更快的计算。但是,如果大量增加速度向量的低维表示的粒子数量,将导致比其他密集运动估计方法更高的计算成本。
考虑流场的时间相关性,有助于将准确帧的信息传播到后续帧。Ruhnau等人(2007)提出一种基于涡度传输方程的流体运动估计方法,使用前一帧的传输涡度场作为当前帧的约束,并考虑了流场间的时间相关性。但信息只能沿一个方向传输,在某些情况下,当前一帧估计不准确时可能导致后续帧的估计结果更差。为了解决该问题,Zuo和Qi(2017)提出一种新颖的时空光学流模型,同时估计流体序列所有帧的速度场。使用该模型可以将准确性估计从具有高对应性的帧传播到相邻帧。
大多数光流法采用全局光流公式估计流场,这种使用全局能量函数约束的方法在流体速度场的不连续边缘上也会进行平滑操作,从而无法保留非均匀流场的空间不连续性。Lu等人(2019)提出一种基于场分割的变分光流方法(field-segmentationbased variational optical flow,FS-VOF),用于保留非均匀流场的空间不连续特性。该方法根据流体的速度分布对粒子图像进行分割,将不连续的流场划分为多个连续的速度场。随后,根据速度在每个分割区域中连续变化并且在区域边界处保留速度场的不连续结构的假设建立平滑约束条件。该方法使用的数据项是基于分割区域的,并且由基于物理的光流方程所推导。
经典的光流方法不能很好地适应具有复杂流动的流体图像,因此使用考虑流体流动特性的物理约束对光流方法的目标函数进行改善,主要是对数据项和正则化项进行改进,以提高流体运动估计的精度。针对流体运动估计的光流模型如表1所示,表中Dt表示湍流扩散系数,?表示速度势函数,ψ表示流函数,Ψ1、Ψ2、γ是比例系数。
表1 针对流体运动估计的光流模型

表1 针对流体运动估计的光流模型
注:Δt为时间采样率,div和curl为求散度和旋度。
2.2 提高对光照变化的鲁棒性
经典的变分光流模型主要依据亮度恒定假设,但是这种亮度恒定约束太过于理想化而无法满足实际情况。传统的HS(Horn Schunck)光流法对光照变化十分敏感,光流的鲁棒性很差。
为了提高对光照变化的鲁棒性,提出了大量基于连续性方程的流体运动估计算法(Uras等,1988;Zhou等,2000;Nakajima等,2003;Arnaud等,2006),将连续性方程应用于光流模型,在亮度变化不大的情况下可以提高流体运动估计的精度,但是在光照变化剧烈的情况下无法进行准确的运动估计。
计算机视觉领域在经典变分光流法的基础上也进行了诸多改进,以期提高对光照变化的鲁棒性,这些改进大致分为4类。
第1类方法是使用高阶恒定性假设扩展依赖亮度恒定假设的数据项。Brox等人(2004)使用梯度守恒假设对亮度恒定假设进行扩展,Papenberg等人(2006)在此基础上引入Hessian恒定假设和Laplacian恒定假设。这种方法仅在两帧图像之间光照变化不大时才可以有效提高对光照变化的鲁棒性。此外梯度守恒假设和Hessian恒定假设具有方向信息,因为对象旋转时可能导致方向改变,因此该方法仅在估计平移运动和发散运动时具有积极影响,而不适用于旋转运动。图像序列中任意像素点的空间梯度可以分解为其范数和方向两部分。当方向信息旋转改变时,梯度的范数保持不变。Papenberg等人(2006)提出将梯度范数作为另一恒定性假设。但这些假设同样不适用光照变化较大的情况,而且对噪声十分敏感。Zhong等人(2017)利用基于梯度不变假设的数据项及一个一阶散度和涡度构成的平滑项提出一种新的2维光流算法,不仅可以在光照变化情况下获得较为精确的估计结果,而且在保持运动场的小散度和涡度结构以及减少异常值方面也更具有优势。
第2类方法是提取图像中的光照不变特征用于数据项中。Zabih和Woodfill(1994)提出了两种非局部参数变换:rank变换和census变换。它们描述了一个签名向量s,该签名向量s对局部图像块内中心参考像素与其周围像素的灰度值关系进行编码。census变换对参考像素与邻域像素间的灰度值大小进行比较,如果小于邻域像素的灰度值则标记为0,反之为1,然后将其连接成一串二进制字符串。Müller等人(2011)将census变换应用于变分光流计算方案,并提出了一种新的光流估计方法,利用两个census变换签名间的汉明距离取代亮度守恒约束形成新的数据项。因为census变换反映的是中心像素与周围像素之间灰度的相对大小关系,因此在单调变化的光照条件下具有不变性。但是,census变换对光照变化的不变性在精度上有所妥协,光流估计的结果不如其他方法精确,并且存在很多缺点,例如对非单调光照变化和噪声十分敏感,丢失了来自邻域的大部分信息,对局部图像块信息描述不完整,无法区分附近的暗区和亮区以及census变换的不变性只是针对平移运动,而对旋转或缩放变换则不具有不变性等。针对以上问题,Ranftl等人(2014)通过对具有不同半径的径向模板进行采样,提出了一种尺度不变的census描述符,实现了在缩放变换下的不变性。该方法通过使用径向采样而不是基于窗口的采样策略,定义了普查变换的一种新变体,可以实现多尺度重采样,从而实现在缩放变换时的不变性。rank变换在单调变化的光照条件下也具有光照不变性,它的签名向量记录了灰度值小于中心参考像素的邻域像素的个数。Yuan等人(2014)将rank变换嵌入到基于TV-L1(total variational with L1 norm,TV-L1)模型的数据项中,提出了一种新的对单调变化的光照具有鲁棒性的光流估计算法。但是与census变换一样,rank变换也不可避免地丢弃了大量的局部图像信息。为了在保持不变性的同时尽可能多地保留局部图像信息,Demetz等人(2013)提出了一种新的rank变换---CRT(complete rank transform)。CRT结合编码完整强度顺序的思想对rank变换进行扩展,它对全部像素的秩进行编码而不再是仅对参考像素的秩进行编码。census变换对不同的局部图像块可能生成相同的签名向量,无法处理中心像素饱和的图像块,Rashwan等人(2013)提出了一种对光照变化具有高度不变性的局部纹理描述子方向梯度直方图(histogram of oriented gradients,HOG)。HOG可以通过产生不同的描述符来检测强度区域的变化。而且,HOG编码可以在一定程度上抑制平移和旋转带来的影响。不过因为生成HOG描述符时依然依赖局部梯度的大小,因此对噪声十分敏感。Mohamed等人(2014)通过修改使用二进制特征描述符(8位描述符)作为匹配成本的局部定向模式(Jabid等,2010),提出了一种对光照变化更加鲁棒的方法,仅对邻域中的方向信息进行编码,而不是强度值,比其他使用强度值的描述符对光照和噪声更鲁棒,但是需要非常高的计算时间。Ali等人(2016)提出一种使用邻域描述符(normalized neighborhood descriptors,NND)作为匹配成本的方法。邻域描述符基于每个像素相对于其相邻像素的自相似性度量,这种成本使得关于一个像素的大部分信息得以保留。该方法相对Mohamed等人(2014)提出的MLDP(modified local directional pattern)方法,计算时间大幅减少,但精度较低,其主要贡献在于实现了对鲁棒性、准确性和计算速度的折衷。Xu等人(2017)介绍了一种称为亮度分布矩阵(brightness distribution matrix,BDM)的新型数据结构,对剧烈变化的光照具有鲁棒性。此外,由于基于BDM的运动估计方法在处理复杂的流体情况时需要进行大量计算,因此为了减少整体运动估计的时间,又基于图形处理单元(graphics processing unit,GPU)开发了该方法的并行版本。
第!类方法是采用结构纹理分解方法进行预处理将图像分解为与图像中主要大对象对应的结构部分和包含精细比例细节的纹理部分然后使用纹理部分代替原始灰度图像进行后续光流计算这种方法期望光照变化导致的阴影和亮度变化等影响主要表现在结构部分而纹理部分则几乎不会受到影响"#$#%等人&''(和)*等人&'+&提出了一种基于全变分正则化,-$*./012#3/456#7*,04模型的结构纹理分解方法对图像进行分解使计算精度显著提高但是只适用于光照变化不大的情况而且计算成本很高袁建英等人&'+8考虑到使用纹理信息进行光流计算在非单调且变化不大的光照下能够提高光流估计精度以及在单调且剧烈变化的光照条件下9#.1-1变换仍然具有恒定特性提出了一种能适应不同光照变化的结合结构纹理分解和9#.1-1变换的光流估计方法利用纹理信息和9#.1-1变换构建新的数据项并根据光照变化情况自适应调整两者之间的权重实现在不同光照条件下自适应选择合适的数据项
第:类方法是建立光照变化的数学模型;#./.#36和
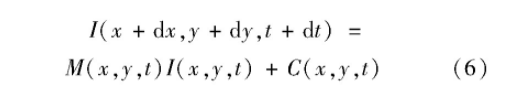
该模型假设在时刻$'$$图像的亮度可以由时刻$图像的亮度和一系列的参数线性化表示这种线性化光照模型相比亮度恒定约束要更松弛允许不太精确的匹配提高了计算结果的精度但是这种方法在运动不连续的情况下没有效果E*7等人&''8在此基础上考虑了更多与光照有关的因素将两个连续图像中的像素亮度通过运动参数)和*以及参数!"#$和%"#$联系起来该方法在运动不连续和光照变化时都可以获得良好的估计但是计算结果的精度与参数的选择有关而且由于公式中包含过多的参数使得优化过程变得十分复杂
大位移估计
光流法使用的变分公式仅限于小位移估计而无法捕捉大的运动为了克服这个问题很多研究者采用多分辨率金字塔方案来处理大位移从而提高运动估计的精度并降低计算的复杂度BF7*.和GF3#H+((@I2?-等&'''J#*6H等&'+'如图&J#*6H等&'+'所示该方案主要通过一系列不同尺度的图像序列来找到运动矢量将当前模型获得的估计值线性化并嵌入到通过对原图像序列进行连续低通滤波和子采样获得的多分辨率金字塔图像结构中然后沿着多分辨率结构由粗到细9?531#/6?/K*.#逐步进行估计该方案期望在每个细化级别上的残余运动场都满足小运动假设
图&L多分辨率金字塔结构J#*6H等&'+'
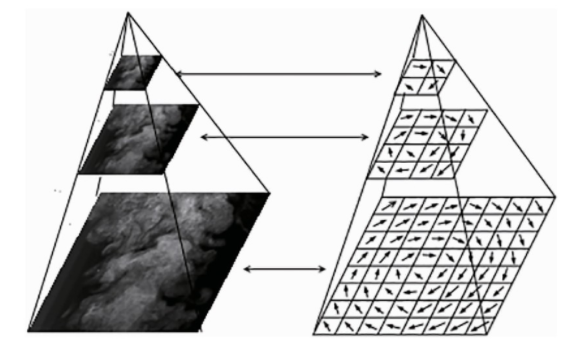
4*=M&LB-%6*/3#1?%-6*?.>N357*$163-96-3#J#*6H#65%M&'+'
虽然多分辨率方案可以解决变分光流算法无法处理的大位移问题但是存在许多问题简单的金字塔方法是将低分辨率图像下求得的运动矢量进行大小调整后作为较高一级分辨率图像的初始运动矢量然后在该较高一级分辨率图像上进一步更新计算结果在这种情况下如果在低分辨率图像上估计运动矢量时出现错误将向下传播到较高分辨率水平而无法纠正此外在金字塔的每一层所有像素的运动矢量都会进行更新这可能导致在给定空间尺度上获取的最佳速度估计在更精细的尺度上被破坏为了解决此问题O566*6*等人+((+提出了一种自适应多尺度方法该方法是基于由粗到细的多分辨率方法的一个拓展方案其引入了一个抑制标志来实现局部自适应离散化在金字塔的每一层对求得的运动矢量进行误差计算以确定每个像素点的运动矢量的可靠性如果误差低于规定的阈值则在相应像素点处设置抑制标志表示该像素点的运动矢量已经足够精确然后对该层获取的运动矢量进行插值作为下一层的初始运动矢量设置抑制标志的像素点在金字塔更高一级分辨率对应的像素点及其4个邻域点被禁止,它们不参与该层的迭代更新而是保持初始运动矢量不变,这可以防止可靠的运动估计被破坏。与简单的金字塔方法相比,该方法可以提供更好的光流估计并且几乎不增加计算成本。
除上述问题外,多分辨率方案还存在其他问题。由于位移的主要成分是在对原始图像进行多次低通滤波和子采样后对应的粗分辨率水平上计算的,因此无法估计精细结构的位移。多次子采样会导致一些薄结构和细小结构的丢失,如果这些精细结构的运动与它们附近区域的运动具有显著的不同,则运动估计算法很难正确获取这些结构的运动。例如在气象图像中,像卷云这样的中尺度结构可能会显示出与低海拔大气层运动完全不同的大位移运动。或者在粒子图像中,由于图像的连续下采样,大速度的小粒子被平滑,从而导致信息丢失和错误的速度测量。
基于相关方法的PIV图像测速方法在估计大位移时具有鲁棒性,为了解决上述问题,Héas等人(2007)和Heitz等人(2008)分别针对气象图像和粒子图像提出了一种将相关方法与光流模型相结合的方法。该方法的主要思想是使用一组基于相关方法获取的密集大尺度位移估计代替多分辨率方案的粗糙速度估计,其在能量最小化函数中增加了一个新的数据约束,使估计的位移接近基于相关方法获取的矢量场。Seong等人(2019)提出一种新的将相关方法与光流法进行结合的混合方法,首先使用最先进的互相关方法来考虑相对较大的粒子位移并插值恢复到原始图像的分辨率,然后利用光流法细化获得的流场。Yang和Johnson(2017)、Liu等人(2020)引入Liu和Shen(2008)获得的基于物理的光流方程,提出了类似的混合方法。这种互相关和光流法的混合方法可以结合每种方法的优点,从而提供一种处理大位移PIV图像以获得高分辨率速度场的稳健工具。
基于速度场小波展开的光流估计方法(Dérian等,2011,2013;Kadri-Harouna等,2013)相对于多分辨率方法也具有其独特的优势。该方法将速度场在小波正交基上进行适当分解,利用各尺度上基函数的线性组合表示速度场的两个运动分量,并且基于小波提出了新的高阶多尺度正则化方法。这种基于小波变换的光流估计方法为多分辨率估计算法提供了一个很好的数学框架,避免了"由粗到细"的多分辨率框架估计大位移时存在的线性问题,而且由于其易于实现高阶正则化,从而提高了运动估计算法的精度和性能。此外小波分解过程能够消除图像序列中存在的一部分噪声。Schmidt和Sutton(2019)对这种方法进一步发展,提出了一种在速度和精度上都有很大改进的基于小波变换的光流方法,采用提升法和对称边界条件实现小波变换,并利用湍流的固有特性、湍流能量谱和半自动启发式算法来优化正则项的加权参数,该参数在以前的光流算法中主要是根据经验确定的。在该方法的基础上,Schmidt和Sutton(2020)又进行了优化,提出了一种在物理上更为合理的正则化方案,提高了速度估计的准确性。该方法使用矩阵乘法替代小波变换方法,简化了正则化方法,比传统卷积或提升方法更有效。
2.4 消除异常值
运动不连续、遮挡和噪声等都会导致异常值的产生,光流法的另一个关键问题就是处理异常值的能力。Horn和Schunck(1981)依赖亮度恒定性和空间平滑性约束提出的经典光流方程采用的是二次函数的形式,而采用这种二次惩罚函数对由反射、遮挡等引起的异常值不具有鲁棒性。不同的惩罚函数及其关联的影响函数如图3(Black和Anandan,1996)所示。从图3(a)所示的二次函数及其关联的影响函数(Hampel等,1986)可以看出,采用二次惩罚函数的光流方程会赋予异常值较高的权重,导致异常值对整体解决方案的贡献"过多".为了提高鲁棒性,减少异常值的影响,Black和Anandan(1996)引入了一个稳健的估计框架来处理异常值,提出了多种基于鲁棒统计的非凸惩罚函数用于替代原本的二次惩罚函数(图3(b)-(d))。不同的惩罚函数具有不同的优势,但共同特点是能够减少异常值的影响。截断二次函数是计算机视觉中最常见的鲁棒惩罚函数之一,从图3(b)可以看出,使用该函数时,误差在固定的阈值内是二次加权的,而一旦超过这个阈值,误差就会达到一个恒定值。通过检验该惩罚函数的影响函数可以发现,在阈值之外异常值的影响为零。而其他的惩罚函数,如Geman-McClure(图3(c))和Lorentzian惩罚函数(图3(d)),在阈值之外,异常值的影响也趋近于零。
虽然这些非凸惩罚函数可以有效减少异常值的影响,并在Roth等人(2009)和Sun等人(2008)的方法中得到了良好的应用,但是其相应的非凸能量函数都很难实现最小化。Bruhn等人(2005)选择了凸型的Charbonnierc惩罚函数(Charbonnier等,1994)来构造能量函数。Sun等人(2010)对凸型Charbonnierc惩罚函数和非凸型Lorentzian函数进行测试,发现在测试集上使用凸型Charbonnierc惩罚函数的算法性能都优于使用鲁棒性较强的非凸型Lorentzian惩罚函数的算法。其中一个原因可能是非凸函数的优化难度较大,导致优化方案局部最优性较差。此外Sun等人(2010)还对广义的凸型Charbonnierc惩罚函数(ρ(x)=(x2+ε2)a,其中x是函数变量,ε是趋近于零的任意正实数)进行了进一步研究,发现当a=0.45时的轻微非凸惩罚函数的性能要比Charbonnier惩罚函数(a=0.5)更好,而当a的取值导致函数更倾向于非凸惩罚函数(如a=0.25)时则无改善。
图3 不同的惩罚函数及其关联的影响函数(Hampel等,1986;Black和Anandan,1996)
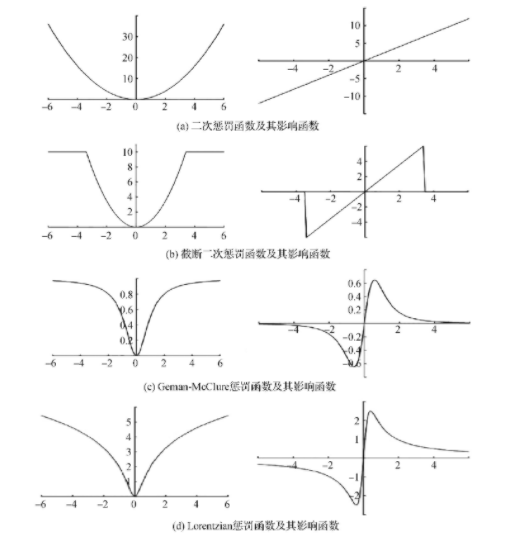
Fig.3 Different penalty functions and their influence functions(Hampel et al.,1986;Black and Anandan,1996)((a) quadratic penalty function and its influence function;(b) truncated quadratic penalty function and its influence function;(c) Geman-McClure function and its influence function;(d) Lorentzian penalty function and its influence function)
Sun等人(2010)发现在"由粗到细"的增量估计过程中加入中值滤波步骤也能有效去除异常值的影响。但是,只是在较大邻域中进行中值滤波具有优势,在以拐角或薄结构为中心的邻域,计算中间值会导致过度平滑。为了解决这个问题,Sun等人(2014)提出了一种新的加权中值滤波模型,但在所有像素上应用加权中值运算增加了计算成本。
诸多方法(Chen和Koltun,2016;Gadot和Wolf,2016;Menze等,2015;Bailer等,2015;Palomares等,2017)执行前向-后向一致性检查去除异常值。对输入的两帧图像分别求得前向光流u F和后向光流u B,然后执行前向、后向一致性检测,即对图像中的每一个像素点x处的前向和后向光流值进行判断,判断的标准为
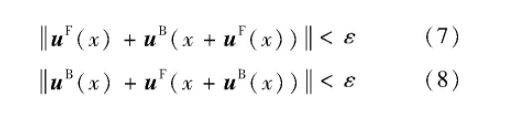
式中,ε为用户设定的一致性检验的误差阈值,若像素点处的前向和后向光流值不满足上述等式,则确认为异常值。
3 结语
基于光流法的流体运动估计技术一直是各领域的研究热点。相比PIV图像测速技术来说,光流法能够获得更加密集的运动矢量场且适用于不同类型图像的运动估计,但是也存在不少困难和挑战。本文从光流法的基本原理出发,对基于光流法的流体运动估计技术进行了综述,阐述了光流法需要解决的4个难点及解决方法。对每一个难点,虽然解决和改进的方法都很多,并且都对流体运动估计的结果有着不同程度的改善,但是依然存在以下需要进一步研究的问题:
1)计算复杂度较高。与PIV技术一样,传统的变分光流法缺乏物理解释。考虑到流体流动的物理特性,不少研究利用流体力学相关知识对光流模型的目标函数进行改进,如引入连续性方程和高阶div-curl正则化等。这些方法虽然能够提高运动估计结果的精度,但是改进后的目标函数形式复杂,计算复杂度高。针对该问题,找到良好的数值求解方法是一项重要的研究内容。
2)大位移估计。大位移估计常用的是基于金字塔的光流方法,但是有其自身的局限性。当位移远大于颗粒尺寸时,该方法不能给出有意义的结果。不少研究提出了基于相关方法和光流法的混合估计方法,结合了相关方法和光流法的优势,可以处理大位移图像并获得高分辨率速度场,但这种方法多限于粒子图像的运动估计,因此将该方法用于其他类型的流体运动图像,是未来值得探索的方向。
3)对光照变化的鲁棒性。亮度恒定假设在光照变化条件下并不能满足,为了提高在光照变化情况下光流算法的鲁棒性,采用了以下4种方法:(1)使用高阶恒定性假设扩展依赖亮度恒定假设的数据项;(2)提取图像中的光照不变特征用于数据项中;(3)采用结构-纹理分解方法;(4)建立光照变化的数学模型。但不同的方法在精度、鲁棒性、计算的复杂度和计算效率方面具有不同的优势和缺陷,针对该问题,可以通过结合不同方法的优势,开发出对光照变化鲁棒的流体运动估计方法。
4)提高计算效率,实现实时估计。光流法需要进行复杂的变分优化,计算效率低下,近年提出的一些GPU并行算法虽然有效提高了计算效率但仍无法实现实时估计,最近发展起来的基于光流神经网络的流体运动估计算法(Cai等,2019),虽然能在一定程度上实现实时性,但缺乏训练集且还不够成熟,因此提高流体运动估计算法的计算效率,实现实时估计仍是未来值得研究的方向之一。
参考文献
[]Adrian R J. 1991.Particle-imaging techniques for experimental fluid mechanics. Annual Review of Fluid Mechanics 23(1):261-304[DOl:10.1146/annurev.fl.23.010191.001401]
[]Ali S,Daul C,Galbrun E and Blondel W.2016. lumination invariant optical flow using neighborhood descriptors Computer Vision and Image Understanding, 145:95- 110[D01:10.1016/j.cviu.2015.12.003]
[]Arnaud E,Memin E, Sosa R and Artana G 2006.A fluid motion estimator for schlieren image velocimetryl/Proceedings of the 9th European Conference on Computer Vision. Graz Austria: Springer:198-210[DOl:10.1007/11744023_ ,16]
[Bailer C,Taetz B and Stricker D .2015. Flow fields:dense correspondence fields for highly accurate large displacement optical flow estimat
ion//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago,Chile:IEEE:4015-4023[DOl:10.1109/ICCV.2015.457]
[]Battiti R,Amaldi E and Koch C.1991.Computing optical flow across multiple scales:an adaptive coarse-to-fine strategy.International Journal of Computer Vision,6(2):133-145[DOI:10. 1007/bf00128153]
[Black M J and Anandan P. 1996.The robust estimation of multiple motions:parametric and piecewise - smooth flow fields. .Computer Visionand Image Understanding,63(1):75-104[DOl:10. 1006/cviu.1996.0006]
[]Brox T,Bruhn A,Papenberg N and Weic kert J.2004. High accuracy optical flow estimation based on a theory for warping//Proceedings of the 8th European Conference on Computer Vision.Prague ,Czech Republic:Springer.25-36[D0l:10. 1007/978-3-540-24673-2_ _3]
[]Bruhn A,Weickert J and Schnorr C .2005.Lucas/Kanade meets Horn/Schunck:combining local and global optic flow methods. InternationalJournal of Computer Vision,61(3):211-231[DOl:10.1023/B:VISI.0000045324 .43199.43]
文献来源:邵绪强,杨艳,刘艺林。流体运动估计光流算法研究综述[J].中国图象图形学报,2021,26(02):355-367.