沉积物间隙水在超纯水采样管内的流动和扩散规律研究

工程流体力学论文范文第三篇：沉积物间隙水在超纯水采样管内的流动和扩散规律研究

　　摘要：对沉积物间隙水在充满超纯水的采样管内的流动和扩散规律的研究是之后对样品进行分析研究的基础。建立了流体运动的数学模型， 利用FLUENT软件中的组分输运模型对质量分数为1%的nacl溶液在水中的扩散进行了仿真。模拟了在一定入口流速下从采样管和间隙水交界处开始的溶液浓度分布规律， 分别讨论了流速梯度及分子扩散对溶液浓度分布的影响， 通过仿真分析验证了理论公式的正确性。

　　关键词：溶液扩散； FLUENT;组分输运模型；浓度分布；

　　作者简介：王凯 （1993-） , 男， 硕士研究生， 主要研究方向为机电液控制及深海探测设备。；

　　Abstract:The study of sediment interstitial water flowing and diffusing through a sampling tube filled with distilled water is the foundation for further research to the samples. Mathematical model of fluid transport was built, the species transport model in FLUENT was taken to simulate this process, while the interstitial water was replaced by nacl solution of which the mass fraction was 1%. The concentration distribution of the solution from the solution-water interface at a specific inlet velocity was simulated. The influence of velocity gradient and molecular diffusion were discussed. The theoretical formula is proved to be correct.

　　Keyword:solution diffusion; FLUENT; species transport model; concentration distribution;

　　在海洋中， 水柱中的颗粒物质沉降到海底形成沉积物的过程中， 部分海水将留存于沉积物颗粒之间的孔隙里， 形成沉积物间隙水。它是海洋生物地球化学循环及全球气候环境演变过程的重要信息载体， 已成为研究海洋物理、化学和生物过程变化的"灵敏指示剂"[1].鉴于海底沉积物间隙水研究的重要性， 国内外对间隙水采样技术进行了大量有益的研究工作， 研制了多种间隙水采样装置。其中， 无动力式渗透泵能够在没有外界提供能源的条件下， 可靠 （结构简单可靠， 既不需要电力， 也没有运动部件） 、自动地实现深海原位、高质量连续时间序列的海底沉积物间隙水样本的采集， 从而为海洋科学研究提供全面、可靠的原始数据。采样管作为渗透泵的关键部件， 对其内部流体迁移和扩散运动的研究是获得高质量时间分辨率样品的关键所在。由于涉及到混合物的扩散及传输， 利用Fluent中的组分输运模型进行仿真模拟， 能够得到间隙水在采样管内扩散的分布规律， 为之后的样品回收和分析提供理论依据。

　　1 系统构成

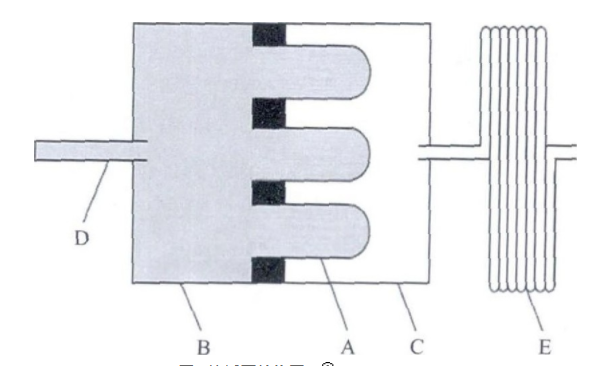
　　渗透泵结构原理图如图1所示， 主体部分被半透膜A分割成两个腔室， B腔充满一定浓度的盐溶液， C腔充满纯水。B腔通过导管D与海水相通。在渗透压的作用下， C腔纯水将透过半透膜A向B腔运动， B腔中多余溶液由导管D排出。同时， 样品采集管E中的纯水向C腔运动以补充C腔纯水的损失。由于样品采集管E中纯水容积减少， 形成局部真空， 样品采集管E的另一端就将间隙水吸入采集管， 从而样品采集管E可连续采集 （或吸入） 间隙水样品。

　　图1 渗透泵结构图

　　2 数学模型的建立

　　通过对无动力渗透泵的原理分析可以建立间隙水在采样管中扩散的理论模型， 即在一定的流速下一种溶液进入到充满水的毛细管内并不断扩散迁移。这种扩散可以认为是由两个方面组成的合成运动：流速梯度引起的分子移动和分子扩散[2].

　　对于由流速梯度引起的分子移动， 可由圆管中的层流运动速度分布公式确定[3]:

　　式中， a为圆管半径；

　　r为距离轴线的距离；

　　μ为动力粘度；

　　J为水力坡度；

　　γ=ρg, 这表明圆管层流运动过流断面上的流速

　　分布呈一个抛物面， 最大速度为轴线处

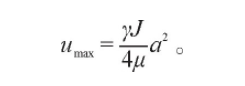
　　对于分子扩散， 由于各点的浓度随时间的变化而改变， 故而使用菲克第二定律。圆管内的流动相对于轴线具有对称性， 将模型简化为沿经过轴线的平面上的一维扩散问题， 在轴线方向上有[4]:

　　求解式 （2） 这一扩散方程， 初始条件为t=0时C=0 （x>0） , C=C0 （x<0） , 边界条件为：

　　t≥0时C=0 （x=∞） , C=C0 （x=-∞） , 求得浓度分布方程为：

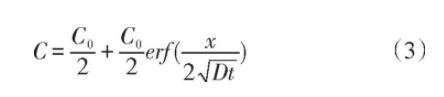
　　式中， C为扩散质的浓度；

　　D为溶液的扩散系数， 扩散系数由实验确定；

　　C0为扩散质的初始浓度；

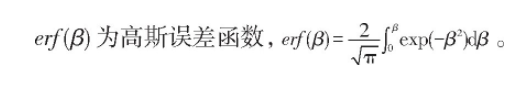
　　3 仿真分析

　　由于溶液与超纯水之间的混合属于分子混合水平上的流体混合， 对于这种混合物的扩散及传输问题， FLUENT提供了通用有限速率模型进行模拟。该模型是基于组分质量分数的输运方程， 反应速率在这种方法中以源项的形式出现在组分输运方程中， 计算反应速度有以下几种方法：层流Arrhenius速度表达式计算、Magnussen和Hjertager的漩涡耗散模型计算、EDC模型计算。通用有限速率模型的应用范围最为广泛， 可以模拟化学组分混合、输运和反应的问题[5].

　　安装到无动力渗透泵上的采样管一般采用内径0.8 mm~2 mm的聚四氟乙烯毛细管， 采样管在布放之前充满超纯水， 布放之后一端插入海底沉积物流体中进行采样， 采样管的长度可以达到数百米并盘成一盘与一系列渗透泵相连[6].通过改变主腔体中溶液的浓度进而改变膜的渗透压或者是改变渗透膜的面积和厚度都能够改变透过膜的水的通量， 进而改变毛细管内液体的流速。现有的Osmo Sampler渗透泵的流速范围可达0.1 m L d-1~12 m L d-1[7].

　　选取采样管末端与间隙水接触的一段作为模型， 模型参数如下：管道直径为1.8 mm, 考察长度为1 000 mm, 管道内初始充满超纯水， 调用FLUENT材料库中h20<liquid>;间隙水人为设置为1%的nacl溶液， 密度为1 005.34 kg/m3, 比热为4 030 j/kg·K, 热传导率为0.6 W/m·K, 摩尔质量为18.1255 g/mol.管道的上下边界采用固壁边界条件， 采用速度入口及压力出口， 在ICEM中完成结构化网格划分， 并在近壁面处细化网格， 网格数目为40 000.

　　由于采样管内液体流速很低， 故而使用压力基求解器， 管道内的液体流速、浓度等物理量处于不断变化的过程中， 采用瞬态计算模型。选择组分输运模型并激活入口扩散， 湍流模型选择层流模型， 入口流速定义为0.002 m/s, 采样管内充满超纯水， 入口处定义为1%的nacl溶液， 完成patch, 计算时间设置为500 s, 在200 s时的nacl溶液分布如图2所示。

　　图2 200 s时nacl浓度分布云图

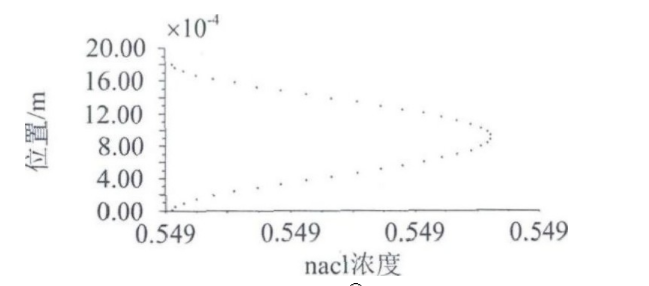
　　在200 s时， 平均速度所在平面位于 处， 在0.4 m处做一径向直线并考察径向浓度分布曲线， 如图3所示。由图3可见， 由于受管内速度分布的影响， nacl浓度分布也呈现近轴线高， 近壁面低的抛物型型分布， 符合式 （1） 的规律， 但轴线处和壁面处的浓度差异很小， 这表明在管内流速很低的情况下， 由流速梯度所引起的分子移动对溶液浓度的影响很小， 可以忽略。

　　图3 200 s时径向浓度分布图

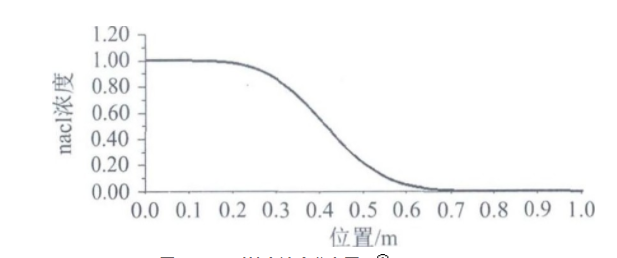
　　同样在200 s时沿轴线处的浓度分布规律如图4所示， 在入口处nacl浓度为初始浓度C0=1%, 随着溶液的移动， nacl溶液逐渐与毛细管内的超纯水混合稀释， 其浓度沿液体前进方向逐渐降低， 直到降低到0.在x1=0.4 m处时nacl质量分数为0.52%, 与理论计算的0.5%很接近， 仿真结果比较准确。这表明在扩散系数一定的情况下， 溶液沿轴线方向的浓度分布呈现与式 （3） 一致的规律。

　　图4 200 s时轴向浓度分布图

　　4 结语

　　研究溶液在充满水的采样管内的扩散规律对于获得渗透泵高质量时间分辨率样品至关重要， 通过对nacl溶液在毛细管内的扩散进行仿真， 可以得到如下规律：

　　1） 溶液在采样管内的扩散受到流速梯度引起的分子移动和分子扩散二者的共同影响， 但在流速很慢的情况下， 流速梯度引起的分子移动的影响很小， 在分析时可以忽略， 分子的扩散起到主要作用。

　　2） 在扩散过程中溶液浓度沿轴线方向呈误差函数规律分布， 首先由浓度为0缓慢增加， 之后增加速度加快， 在平均速度通流截面处浓度变化最大， 此时的浓度大约为初始浓度的一半， 之后浓度变化减缓直到管内完全充满与初始溶液浓度相同的溶液。浓度分布沿平均速度处对称分布。

　　参考文献

　　[1]Houghton, J T, Y Ding, D J Griggs, et al.Intergovernmental Panel on Climate Change （IPCC） third assessment report.USA:CambridgeUniversity Press, 2001.

　　[2]Sir Geoffrey Taylor.Dispersion of soluble matter in solvent flowing slowly through a tube[J]. 1953.

　　[3]禹华谦。工程流体力学（水力学） [M]成都：西南交通大学出版社， 2007.

　　[4]闻德荪。工程流体力学。水力学[M]北京高等教育出版社， 2004.

　　[5]朱红钧。Fluent15. 0流场分析实战指南[M]北京：人民邮电出版社， 2015.

　　[6]Hans W.Jannasch, Earl E. Davis, Miriam Kastner. CORK- I :Long-Term monitoring of fluid chemistry, fluxes, and hydrology in instrumented boreholes at the Costa Rica Subduction Zone[J].Proceedings of the Ocean Dirilling Program, 2003.

　　[7]Hans W.Jannasch, C. Geoff Wheat, Josh N Plant. Continuous chemic al monitoring with osmotic ally pumped water samplers:Osmo Sampler design and applic ations[J]. Limnology and Oceanography:Methods 2004:102-113.