热力学第二定律的热机效率问题研究

　　摘要：统计力学认为， 孤立系统的一个叫做熵的物理量又随着时间逐渐增大的过程， 直到达到一个最大熵状态。有科学家把这个结论推广到整个宇宙， 得到结论说宇宙最终会达到一种热寂的最混乱的状态。虽然也有人认为这个结论不能推广到整个宇宙， 但是这个判断的理由也是牵强的。根据传统的热力学理论， 我们不能自然的避免宇宙趋向热寂。实际上， 传统的熵增定律是在忽略了万有引力的基础上得到的， 而在天体级别的大范围内， 万有引力起到了非常大的作用， 这时候引力作用将使得热力学第二定律得出的熵增定律不再一定成立。本文将设计一个理想实验证明之。

　　关键词：热力学第二定律； 熵； 热寂； 万有引力；

　　1 引言

　　热力学第二定律是最初是讨论热机效率的问题而引入的， 克劳修斯和开尔文分别表述了该定律的不同但等效的两种形式。后来统计物理引入一个物理量熵S, 用孤立系统熵增原理做了简洁的表达。关于这个结论是否可以推广到整个宇宙， 人们有不同的看法， 但立论都显得牵强。下面本文引入一个理想实验， 来讨论这个问题。

　　2 理想实验

　　设宇宙空间离开其他天体很远的一个范围内， 存在一个半径为r的巨大球体， 里面充满了一种单原子理想气体， 气体均匀分布， 压强为P0, 温度为T0, 总质量为m, 摩尔质量为M, 热容常数。对这团气体， 如果不考虑万有引力， 它自然要不断的膨胀， 最后体积不断变大， 熵S也不断增加。但是如果考虑万有引力， 只要气体的总质量足够大， 使得气体在引力的作用下塌缩， 考虑这时S的变化情况。

　　根据统计力学， 对理想气体的熵， 有下面的公式

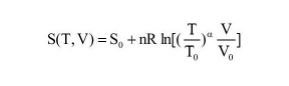
　　其中n是气体物质的量， R为理想气体常数。

　　如果要求熵减即S<S0, 则只需要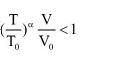

　　现在考虑初始状态开始的一段无限小过程， 此时气体半径减小dr, 温度升高d T, 为了简化计算， 假定这时气体的温度和密度都是均匀的--实际上气体的温度和密度会有一个球对称的不均匀分布， 但这时的熵会更低。

　　这个过程万有引力做功等于初态和终态引力能之差。对于质量为m半径为r的均匀球体的引力自具能：

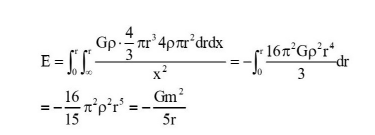
　　由能量守恒定律， 该过程引力做功：

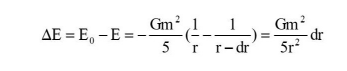
　　又理想气体内能与温度有如下关系：U=an RT

　　则：

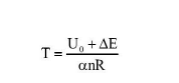
　　则有：

　　于是只要满足：

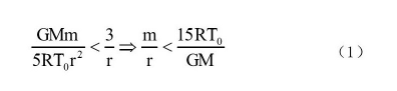
　　这个过程就是熵减。

　　考虑到气体必须还要在引力作用下塌缩， 就要求处在气团边缘的气体不能逃逸引力的作用。于是有：

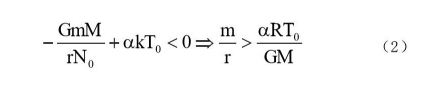
　　对于单原子气体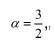， , 所以 （1） 和 （2） 式可以同时成立， 于是该孤立系统自发熵减。

　　3 讨论

　　从上面的计算， 可以看到理想实验证明孤立系统在考虑万有引力的情况下是可能熵减的。虽然熵减成立的范围因为方程式 （2） 的约束仅在有限的范围内成立。但是考虑到方程式 （1） 已经做了较大的简化， 所以成立范围被缩小了。另外， 在宇宙大范围内的星际尘埃在万有引力下塌缩形成恒星的过程， 在相当大的范围内还没有生成元素和气体， 所以在塌缩之初并不受方程式 （2） 的约束。所以， 如果恒星最初是由广大的星际尘埃在万有用力作用下塌缩形成的话， 系统熵减就是一个比较普遍的过程。

　　4 结束语

　　从以上的讨论， 笔者得出结论， 宇宙中孤立系统也会有熵减过程。当然， 在宇宙实际状态下， 必须重新定义熵的表达式， 因为在元素形成之前， 熵还没有很好定义。但是就熵的字面意义即混乱度来说， 直观的也能得出混乱度减少的结论。宇宙或许可以逃脱热寂的魔咒！

　　参考文献
　　[1]L.E.雷克。统计物理现代教程[M].北京大学出版社， 1983 （04） .
　　[2] 林宗涵。热力学与统计物理学[M].北京大学出版社， 2007 （01） .
　　[3]苏汝铿。统计物理学[M].高等教育出版社， 2004 （02） .