上海迪士尼乐园游玩项目优化选择方法研究
摘 要:上海迪士尼乐园是中国大陆第一个迪士尼主题公园,大量游客使得园区变得拥挤,排队等待耗费许多游玩时间,严重影响游园者的体验。文章建立了上海迪士尼乐园游玩项目选择优化模型,在传统蚁群算法的基础上,将项目游玩时间、等待时间、喜好度等信息引入路径选择机制及信息素调节机制,实现游玩时间一定的条件下喜好度最大的游玩方案选取。
关键词:路径规划;蚁群算法;迪士尼
引言
迪士尼乐园作为世界顶级娱乐休闲主题公园,其无处不在的新奇、刺激和冒险游乐项目,带给人们无穷无尽的快乐和欢笑,吸引游客去开启梦想[1].据上海申迪集团(中方股东)预测,2016 年全年游客数可能会达到 1000 万。分析师的对该项数字更为乐观,他们认为全年游客数将高达 1500 万[2].这会使绝大部分项目的排队等候时间变长,从而影响游园体验。
由于上海迪士尼乐园推出了一款官方 App,可以在上面方便地查阅到各个项目游玩的等待时间。基于这些动态数据和项目游玩时间、项目间距离等已知数据,本文将建立一个可以方便地规划游玩方案的数学模型,使游客们的需求得到最大限度的满足。
上海迪士尼乐园由“探险岛”“明日世界”“宝藏湾”“梦幻世界”“奇想花园”和“米奇大街”六大主题园区组成。每个主题公园有多个游玩和娱乐项目,如探险岛主题园区的翱翔-飞越地平线、古迹探索营、欢笑聚友会的丛林迪士尼朋友们、雷鸣山漂流、人猿泰山-丛林的呼唤等,全部游乐项目大约 40 个。
1 模型假设
(1)各项目所需的排队时间和游玩时间已知,游乐项目的等待时间由排队人数决定;(2)任意两个项目间都可达,且路已知;(3)游客的步行速度为常数,从一个项目到另一个项目之间所需时间由两个项目间的距离决定。
2 模型的建立与求解
2.1 模型建立
2.1.1 目标函数确定
引入路线规划决策变量 xijxij=1,经过 i 到 j 的路段0,不经过 i 到 j 的路段用 H 表示路线规划上游客对各项目喜好程度的总和,则max H=ni=1Σnj=1Σhixij。
2.1.2 约束条件确定
假设游客当天准备游玩时间为 M,实际游玩时间用 T 表示,由于 T=路径时间+排队时间+游玩时间=路径时间+停留时间,因此用函数表示为:
T=ni=1Σnj=1ΣTSij·xij+ni=1Σnj=1ΣTi·xij由于每个项目只能有一条边出去,所以nj=1Σxij=1 或 0,i=1,2,…,n同理,每个项目只能有一条边进去,所以ni=1Σxij=1 或 0,j=1,2,…,n我们建立如下的线性规划模关键词:路径规划;蚁群算法;迪士尼。

2.2 模型求解
2.2.1 路径构建随机比例原则[3]:对于每名游客 k,路径记忆向量 Rk按照访问顺序记录了所有 k 已经经过的项目序号。设游客 k 当前所在项目为 i,则其选择 j 项目作为下一个访问对象的概率为:
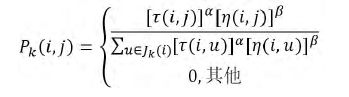
其中 Jk(i)表示从项目 i 可以直接到达的且不在游客访问过的项目序列 Rk中的项目集合。η(i,j)是一个启发式信息,η(i,j)=1d.τ(i,j)表示边(i,j)上的影响因子。α 是表征影响因子重要程度的参数,β 是表征启发式因子重要程度的参数。
计算好概率后每名游客再根据轮盘赌算法则选取访问项目,即产生一个随机数,选择概率与该随机数最接近的项目游玩。
2.2.2 影响因子更新[4,5]
影响因子的更新有两个步骤:首先,每一轮过后问题空间中的所有路径上的影响因子都会衰退,我们为所有边上的影响因子乘上一个小于 1 的常数。随后所有的游客根据自己构建的路径长度在他们本轮经过的边上进行分享。游客构建的路径越短、分享的就越多,影响因子就越大;一条边被游客走过的次数越多,它所获得的影响因子也就越大。项目 i 与项目 j 的相连边上的影响因子值 τ(i,j)按如下公式进行更新:
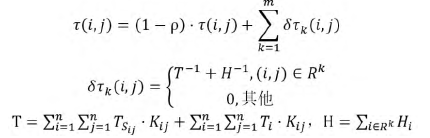
这里,m 是游客个数;ρ 是影响因子的衰退率,规定 0<ρ≤1.δτk(i,j) 是第 k 名游客在经过的边上进行分享的影响因子值,Ck表示路径长度。
在算法初始化时,需要将问题空间上的所有边上的影响因子都被初始化为 τ0,这里我们用 τ0=mCnn来计算,m 是游客个数,Cnn是由贪婪算法构造的路径长度。
这里,m 是游客个数;ρ 是影响因子的衰退率,规定 0<ρ≤1.δτk(i,j) 是第 k 名游客在经过的边上进行分享的影响因子值,Ck表示路径长度,H 是路线规划上中游客对各项目的喜好程度总和。
通过官方 App 查出相关数据代入模型计算,在 8 个小时的游玩时间内最多可以玩到 6 个喜好度最大的游玩项目。
3 结束语
很多游客往往会因为没有规划好合理的路线而玩不尽兴,当时间有限制的条件下不能去更多的项目游玩更喜欢的项目,这就要我们制定合理的路线规划,满足自己的旅游需求,玩到更多的项目。
本文在用蚁群算法解决 TSP 问题的基础上加以改进分别得到了一个限时返回起点游玩喜好程度尽可能大且游玩项目数尽可能多的模型。
本文游玩路线规划的优化设计,不仅在省时方面做到最优考虑,还考虑到了游客对不同项目喜好程度不同,设计出了尽可能游玩更多游客更喜欢的项目的路线规划。站在了游客角度思考问题,为游客设计了最满意最省时的旅游线路。由于蚁群算法的使用,大大降低了运算的时间复杂度,使得如此复杂度的运算程序可以快速得到结果,这是本文的优点。本模型的不足之处是数据采集不太准确,项目游玩时间和游玩等待时间是根据官方 App 提供的数据估计得到,项目之间距离从百度地图推算得出,项目喜好程度是基于对一些同学调查和朋友的调查得到,不具有广泛代表性。
参考文献
[1]上海迪士尼度假区官方网站[EB/OL].https://www.shanghaidisneyre-sort.com/
[2]卢晓明。上海迪士尼的火爆拯救不了迪士尼的业绩?[EB/OL].http://edu.163.com/16/1112/00/C5KPBR5400294MA1.html
[3]方霞,曹洁,张平风。求解较大规模 TSP 问题的改进蚁群遗传算法[J].科技创新与应用,2016,27:10-11.
[4]姜坤霖,李美安,张宏伟。面向旅行商问题的蚁群算法改进[J].计算机应用,2015,35:114-117.
[5] 桂传志 . 混沌优化算法在 TSP 问题的应用 [J]. 科技创新导报,2016,21:74-75.