高数成绩对后续课程成绩的相关性作用

　　1 问题的提出

　　高等数学是信息类土科学生的基础课程，因为信息类行业，得到的结果大多数是物理性结论，都是通过数学公式推导得来的，没有数学就没有结论.由此可见，高等数学这门课程在信息类学校中的地位是很重要的.在通信土程令业中，主干课程有电路分析基础、通信原理、模拟电子线路等.在该令业中，高等数学学得如何，将直接影响学生后续课程的学习，但这一认识只是凭主观经验和定性分析，实证和定量分析极少，这里研究的目的，是以电路分析基础、通信原理、模拟电子线路3门课程学习情况对高等数学学习的影响为例，运用相关系数分析方法，分析和探讨高等数学对后续课程学习的影响，以便为通信土程令业的学生学习提供一些理论依据.

　　2 高等数学成绩对后续课程成绩的相关性影响

　　为分析高等数学成绩对后续相关课程成绩的影响，针对10级通信土程令业326名学生的考试成绩数据进行了抽样追踪调查.在该研究的统计分析中，仅以高等数学成绩与电路分析基础、通信原理、模拟电子线路3门课程成绩为例进行分析，同时一用散点图来表明它们之间的相关影响，见图1一3.

　　2.1 高等数学与电路分析基础成绩关系分布

　　高等数学成绩与电路分析基础成绩散点图如图1所示

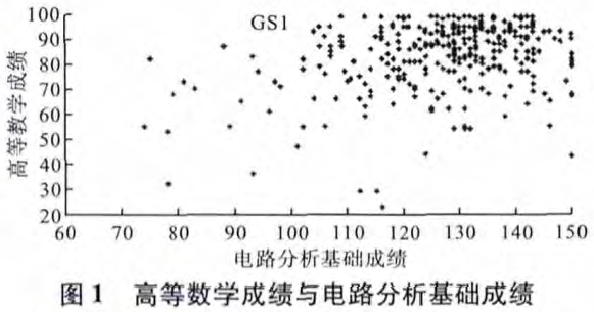
　　从图1可以看出，绝大多数高等数学成绩较好的学生电路分析基础的成绩也较好，而高等数学不及格的学生电路分析基础出现不及格的学生有4名，但高等数学成绩在80分以上，电路分析成绩却在90分以下(满分150分)的同学是值得关注的.由图1也可以看出，具有较好的高等数学成绩的学生倾向十有较好的电路分析基础成绩;具有较差的高等数学成绩的学生倾向十有较差的电路分析基础成绩.可见，学生的高等数学成绩与电路分析基础成绩之间存在密切的关系.

　　2.2 高等数学成绩与通信原理成绩关系分布

　　高等数学成绩与通信原理成绩散点图如图2所示

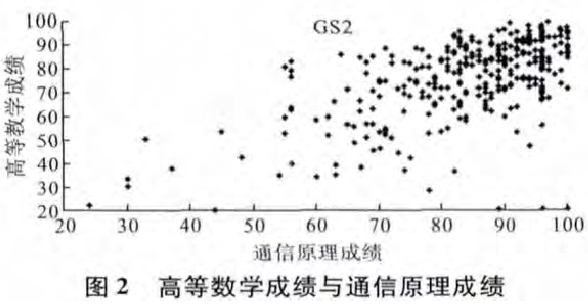
　　从图2可以看出，绝大多数高等数学成绩较好的学生通信原理的成绩也较好，而高等数学不及格的学生通信原理成绩不及格的学生有13名，但高等数学成绩在60分以下，通信原理成绩却在90分以上的同学有8名.由图2也可以看出，高等数学成绩较好的学生通信原理成绩也较好;高等数学成绩较差的的学生通信原理成绩也相对较差.可见，学生的高等数学成绩与通信原理成绩之间存在密切的关系.

　　2.3 高等数学成绩与模拟电子线路成绩关系分布

　　高等数学成绩与模拟电子线路成绩散点图如图3所示

　　从图3可以看出，绝大多数高等数学成绩较好的学生模拟电子线路的成绩也较好，高等数学不及格的学生模拟电子线路成绩不及格的学生有7名.而高等数学成绩在80分以上的学生模拟电子线路成绩不及格的学生有4名，高等数学在60分以下的学生模拟电子线路成绩在90分以上的有5名.由图3也可以看出，具有较好的高等数学成绩的学生倾向十有较好的模拟电子线路成绩;具有较差的高等数学成绩的学生倾向于有较差的模拟电子线路成绩.可见，学生的高等数学成绩与模拟电子线路成绩之间存在密切的关系.

　　3 各科成绩相关性检验

　　相关性是表征2个随机变量或2路信号之间统计关系强弱的指标，如果1个随机变量随着另外1个随机变量的增大而增大或者一减小而减小，则该2个随机变量呈正相关关系;反之，如果1个随机变量随着另外1个随机变量的增大而减小或者一减小而增大，则该2个随机变量满足负相关关系.由相关性引出了相关性系数，相关性系数在一定程度上反应了变量之间的相关性.因此可运用相关性系数分析，寻找其共性，进行对比研究与信息再利用.该研究采用的相关系数的通用公式为

　　相关系数绝对值愈大(愈接近1)，表明变量之间的相关程度愈高;相关系数绝对值愈小，表明变量之间的相关程度愈低.相关系数为零时，表明变量之间不存在相关关系.下面对高等数学与电路分析基础、通信原理、模拟电子线路课程成绩的相关性进行检验.和Y是2组数据，相关系数的计算方法为:分母为归一化系数，因取平方和，总是正数相加，可得最大值.分子为X减去它的均值与Y减去它的均值积之和.当2个差值符号相同时一积为正值，当2个差值一正一负时一积取负值.当X表示高等数学成绩和Y表示电路分析基础成绩时，有4种典型情况:①若高等数学成绩好，电路分析基础成绩也好时，则积为正值，对相关系数做贡献.②若高等数学成绩好，电路分析基础成绩不好时，则积为正值，也对相关系数做贡献，这是该研究不希望的.③若高等数学成绩好，电路分析基础成绩不好时，则积为负值，为降低相关系数做贡献，这是该研究最不希望的.④若高等数学成绩不好，电路分析基础成绩好时一，则积为负值，也为降低相关系数做贡献，这是该研究非常希望的.如③、④部分的绝对数值大，相关系数就小，如果这种小是由第4部分造成，这说明高等数学成绩较差的学生成绩得到提升.但如果这种减小是第3部分造成的，则说明高等数学成绩较好后续课程成绩变差了，这是值得注意的.这时一不能将高数成绩不好归为学生入学成绩降低了，而是需要对相关系数的构成作做一步的分析研究.通信原理、模拟电子线路关系大致相同.为此，以函数X和鱿的2组数与均值的差值之积进行排序，将数据分为4组:①取较大正值者;②取较小正值者;③取绝对值较大的负值者;④取绝对值较小的负值者。

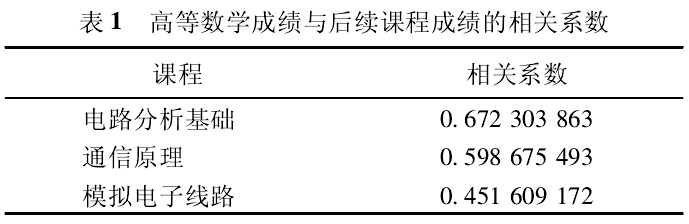
　　从上述步骤分析得出高等数学成绩与后续课程成绩的相关系数见表1.

　　4 结论

　　通过高等数学对后续课程成绩相关性分析，得出以下结论:

　　1)高等数学的学习与各令业基础课的相关性较好，学好高等数学对后续课程的学习至关重要.其中电路分析基础最强，通信原理次之，模拟电子线路最弱.

　　2)为保证学生对后续课程的学习，建议学校加强对新入学学生的学习态度、学习习惯、学习能力等方面的培养，因为这些方面对后续课程学习有着重要的影响.

　　3)因研究样本的采集有一定的局限性，只是以326名学生高等数学成绩为依据的，故样本的代表性还有待提高.

　　参考文献
　　[1]梁好翠.高师数学三门主干课程对后续课程学习影响的分析[J]广西高教研究,2000(1):45-47
　　[2]徐维.超相关系数研究综述[J]广东工业人学学报,2012,29(3):12-17
　　[3]张川.强关于相关系数的探讨数学的实践与认识,2009(19):104-109