2.利用微课解疑导悟,体现灵活性。
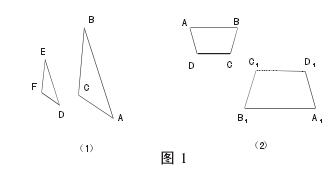
[解疑导悟]例 1.任意画一个三角形,通过作位似图使它各边放大为原来的 2 倍,并写出你的作图步骤。
例 2.确定下列各组位似图形的位似中心。
设计意图:位似作为一种变换方式,在教材中呈现的内容少而精,只见相应的主题图、几个问题等,需要教师适时适度地对教材二次加工,特别是对课本例习题进行合理变式与拓展。要把有关的知识碎片连成片,发挥数学习题的“教学功能”和“发展功能”[3].通过典型例题研习不仅可以检查“导学”情况,而且可以填补教材的“空白”,弥补课本未曾安排例题的缺憾。如果说设疑导学中的微课是“必备动作”,那么在解疑导悟中的微课就是“自选动作”.在这里适时安排微课主要是帮助学生按需灵活选择学习,微课通过题目的合理变式与延伸,拓展教材深度和广度,其目的既可查缺补漏,又可建立联系、整合知识、总结方法、渗透思想、激活经验。
3.利用微课质疑导用,凸显层次性。
[质疑导用]投影:阅读材料,解答问题。
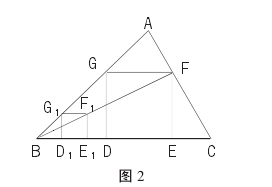
已知:锐角△ABC,如图 2.求作:正方形 DEFG,使 D,E 落在 BC 的边上,F、G 分别落在 AC、AB 的边上。
作法:(1) 画一个有三个顶点落在△ABC 两边上的正方形 D1E1F1G1;(2)连结 BF1并延长交 AC 于 F;(3)过 F 点作 FE⊥BC,垂足为点 E;(4)过 F 点作FG∥BC,交 AB 于点 G;(5)过 G 点作 GD⊥BC,垂足为点 D;则四边形 DEFG 即为所求作的正方形。
问题:(1) 说明上述所求作的四边形 DEFG 为正方形的理由。
(2)上述作图属于哪种作图方法?
(3)在△ABC 中,如果 BC=120,BC 边上的高为80,求上述正方形 DEFG 的边长。
(4)若把(3)中的正方形 DEFG 改为矩形 DEFG,且 DG= 2GF,其他条件不变时,此时,GF 是多少?
设计意图:本题将常规题改编成阅读题,并串以不同梯度的问题,主要考查学生掌握新知、联系旧知、活用新知的能力。在教学中,教师要用活用足教材,除了做到把知识在课内渗透,还要把学生能力触角由课内延伸到课外,让每一个学生都能有所进步。微课是一个将学生引入自我学习的有力手段。此处安排微课主要是激发学生学习潜能,激励学生学会自我超越,并满足不同层次学生的学习需求,培养学生主动获取知识的能力,打破“唯本为纲”的教学禁锢。让学生在微课中,学会主动地建构自己的知识、技能、方法、经验体系,从而使课堂因拓展而流光溢彩,使学生因微课而学有所成。