摘要:作为一门传统上男生占优的学科,数学学习上的性别差异长期以来为许多研究者所关注。而近年来,越来越多的研究显示,男女学生在数学学习上的差距正逐渐缩小,并且在一些数学内容上,女生的表现甚至超越男生。已有的对男女学生在数学学习上的差异研究大多关注的是两者间的整体表现差异,或是在某个内容上的局部差异。本研究从2 000万名初中学生中,随机选取1 000名男生和1 000名女生,根据他们在网络在线学习平台上的答疑数据,分别以章和节为单位,运用多元线性回归模型探索男女学生在初中数学的各项内容上的需求差异。结果发现,在初中三年总共29章的数学内容中,女生在4章内容上有明显高于男生的答疑需求(集中在函数和平面几何上),而男生仅在“概率初步”上有更多的答疑需求。进一步以节为单位的分析显示,男女学生的答疑需求量存在明显差异的节的数量基本持平,而男生占优的节点集中在九年级,女生占优的节点多在七年级。此外,女生需要更多帮助的知识点的平均难度要高于男生。
关键词:教育公平; 性别差异; 数学学习; 多元线性回归;
An Analysis of Gender Differences in Middle School Mathematics Learning Difficulties
ZHU Yan NI Lyu NI Ming
School of Teacher Education, East China Normal University School of Data Science & Engineering, East China Normal University East China Normal University Press
Abstract:As a traditionally stereotyped male subject, gender differences in mathematics learning have long been a major global concern. However, in recent years, research revealed that the gender differences in mathematics learning were shrinking gradually. The existing investigations about the gender differences in mathematics learning mainly attended to the overall differences between the two groups, or the partial differences on a particular content. A group of 1000 boys and 1000 girls were selected randomly from 20 million middle school students for the present investigation. Based on these students' data from an online-question-answering learning system, this study explored the differences on middle school mathematics learning needs between boys and girls via a multiple regression model with chapters and sections as analysis units, respectively. The results showed that in a total of 29 chapters of middle school mathematics learning contents, girls had clearly higher help-seeking demands on 4 chapters(mainly function and plane geometry) and boys had higher demands only on “preliminary probability”. A further analysis revealed that the numbers of sections on which each gender had obviously higher demands were nearly equal, while the chapters favorable to boys were more at the ninth grade and those favorable to girls were more at the seventh grade. In addition, the average difficulty level of the contents girls need more help with is higher than that for boys.
一、 数学学习中的性别均衡
教育均衡是几乎所有国家都在重点关注的一个基础性问题,无论是发达国家、转型国家,还是正处在发展中的国家。在我国,教育均衡更是义务教育法的方向性要求,是实现教育公平的内核,具有重大的现实意义和深远的历史意义。同样地,***主席在十九大报告中也着重强调要“发展素质教育,推进教育公平”。教育失衡是对人的潜能的一种浪费。格拉布(Grubb)、雅尔(Jahr)、诺伊米莱(Neumüller)和菲尔德(Field)指出,均衡既是一个社会性问题,也是一个个体性问题。[1]还有学者提出,教育失衡及其众多后果并非是随机的,而是在很多方面受到来自群体的影响。而失衡对于不同人群的影响,其效应程度也往往是不同的,通常对弱势群体所产生的负面影响会更大一些。从这个意义上说,群体性的失衡比那些由随机因素或个体因素引起的失衡,其危害性可能更为严重。
在数学教育研究领域中,关注均衡问题起始于性别这一主题,之后在其基础上又拓展出对均衡问题其他维度的诸多研究。[2]事实上,性别均衡成为数学教育的热点议题至少已有30年的历史。早在第六及第七届国际数学教育大会上,国际妇女与数学教育组织(IOWME)就主持了两个重要的有关性别与数学的专场。这两个专场最终形成了两本较有影响力的专著,即伯顿(Burton)的《性别与数学: 一个国际性视角》(Gender and Mathematics: An International Perspective)[3]与罗杰斯(Rogers)和凯泽(Kaiser)的《数学教育中的公平: 女性主义与文化的影响》(Equity in Mathematics Education: Influences of Feminism and Culture)[4]。这两本书所提出的理论观点对后续的相关讨论产生了重要的影响,尤其是他们将性别研究中的均衡概念与更一般的社会问题讨论相联系,超越了单一从生理角度剖析数学中的性别差异的做法。而格罗夫斯(Grouws)主编的第一本《数学教与学研究手册》(Handbook of Research on Mathematics Teaching and Learning),也邀请莱德(Leder)撰写了关注性别问题的专门章节,这可以看成是数学教育共同体接纳这一专题的重要一步,其中讨论了促成性别差异的各种不同因素。[5]
在另一方面,数学在传统上被视为一个男生的领域。例如,麦科比(Maccoby)和杰克林(Jacklin)回顾了近1600个有关性别差异的研究,总结认为男生在数学和自然科学上表现更佳,而女生则在阅读和写作方面表现更优。[6]之后的研究者使用了更为复杂的元分析手段,同样揭示了类似的性别差异,但差距似乎在缩小[7][8],有些学者甚至发现性别差异已消退[9][10]。例如,在分析了1990—2007年间发表的关于美国青少年学习的242项研究中的数据后,林德伯格(Lindberg)、海德(Hyde)、彼得森(Petersen)和林(Linn)发现在数学表现上不存在性别差异,而且男女学生的内部差异也几乎一致。[11]
尽管男女学生的数学表现在大体上越来越相近,甘利(Ganley)和卢宾斯基(Lubienski)提出,在测试与课堂教学内容关联较少的数学内容时,男女学生的差异会更易显现出来。[12]赖莉(Reilly)、诺伊曼(Neumann)和安德鲁斯(Andrews)甚至认为,男女学生的差异不在于一般的智力层面,而更多地体现在专门的认知能力上。[13]D.博耶尔(Voyer, D.)、S.博耶尔(Voyer, S.)和布莱登(Bryden)的元分析进一步显示,空间视觉上的性别差异在幼年期时较小,逐步成长到青少年和成人时期,差异会变得越来越大。[14]
瓦特(Watt)指出,很难发现一个比数学能力上的性别差异更具争议性的内容。[15]埃利森(Ellison)和斯旺森(Swamson)将确定数学成就上的性别差异的准确大小的复杂性归于不同测试及不同国家间存在的高度多样性。[16]类似地,林德伯格、海德、彼得森和林认为,数学成就上的差异与样本及结果量度有关。[11]卢宾斯基、鲁宾逊(Robinson)、克兰(Crane)和甘利提出,各种测试的不同用途可能是使性别对学生数学成就的影响变得复杂的另一个因素。[18]
中国也不例外,数学也在传统上被视为男生占主导的一个领域。例如,2009年入选的16位数学学科中科院院士皆为男性。[19]截至2017年4月,女性中科院院士的比例仅为6%。在近20年的国际数学奥林匹克(IMO)中,中国队参赛选手共120人,女生只有2人。在第60届IMO中,包括中国在内获得前三名的国家的所有参赛队员都是男生。回顾2017年的高校新生男女比例也不难发现,在对数学有较高要求的理工类大学中,男生比例明显高于女生,例如清华大学为2∶1,浙江大学为7∶5,大连理工大学为7∶3等。这些都表明,中国的数学领域存在着很大的性别差异。然而,一些中国学者强调:“中国的数学教育缺乏基础性资料,像男女学生数学学习差异这样的课题,应当视为基本国情去进行调查和研究。”[20]相信只有清楚了产生差异的机理,才能更好地诠释性别差异,并进一步帮助所有学生提升他们的数学学习成就。
通过分析2 000名初中学生的数学学习需求,本研究将从数学内容的角度,揭示男女学生在数学学习上的差异。以往的同类研究,大多是从男女学生数学学习的总体表现差异入手,亦或是针对某个专门的数学内容考察男女学生的局部差异。本研究将覆盖学校数学学习中初中三年所有教授的内容,尝试探究男女学生在数学学习难点上的异同,结合文献分析这些异同的成因,为设计更为优化的教学从而实现初中数学的均衡教学提供科学而详实的实证依据。
二、 研究方法
本研究中的数据来自一个专注于中小学互联网教育的学习平台,学习者通过安卓或IOS系统进入该平台参与学习。该平台的用户覆盖我国各地区,在获得数据时,已累计约有6 000万个登记用户,累计使用次数约4亿次。本研究关注的是在该平台上参与数学学习的所有初中学生,总体规模为2 000万左右。本研究从中随机选取了2 000名学生的数据,男女学生各占50%。这些学生在学习平台上的答疑数据是本研究的基础数据。
参照初中数学教材(人教版)的章节目录,本研究首先将初中三年覆盖到的700多个数学知识点归位到人教社教材设置的29章83节上,并以此结构对被选的2 000名男女学生在各知识点上的在线答疑频次进行编码,形成本次分析所需的工作数据。结果共生成以章为单位的58 000个数据点(即29× 2 000) 和以节为单位的166 000个数据点(即83×2 000),每个数据点对应的是某个被选学生在某一章或某一节上的答疑频次。
由于本研究不仅考察初中男女学生各自群体内部的数学学习难点,同时也关注这两个群体间是否在局部的知识结构中存在差异,因此多元线性回归模型成为本研究的核心分析手段。具体来说,即将全体被选学生在某一特定的章或节上的答疑频次设为因变量Y(频次矩阵),个体学生是否在某章或节上点击答疑设为自变量X,学生的性别设为自变量Z,从而利用线性回归模型探索Y与X和Z之间的关系:
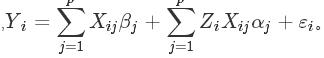
需要说明的是,Zi所表示的个体学生的性别,女生设为-1,男生设为1;协变量Xij表示第i个学习者是否在第j章或节上进行答疑,进行答疑设为1,否则设为0,因此X是29维或83维的一个向量矩阵;βj是第j个协变量Xij的效应值(可视为对应章或节的难易程度);αj是第j个协变量Xij与性别因素的交互效应值;p是总的章数(即29)或节数(即83);而εi是误差值,其分布服从正态分布N(0, σ2)。
本研究首先通过描述性统计,分析比较在哪些章或节上男女学生在答疑频次上存在差异,即对男女学生在各章或节上的答疑频次分别计数。随后,本研究探索在这两组频次次序出现差异的章或节上,男女学生的差异程度究竟如何。具体做法是,通过逐步回归分析,在候选模型中选择AIC信息统计量取得最小值的模型,以权衡估计模型的复杂度和此模型拟合数据的优良性。在最优的回归模型中,取得非零值的交互效应值αj所对应的章或节,即为男女学生在学习难点上存在明显需求差异的章节。
三、 研究发现
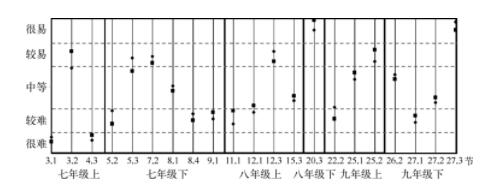
在初中三年总共29章的数学内容上,男女学生的答疑频次位列前三位和末三位的知识内容是完全一致的(见图1)。具体来说,七年级上学期的首两章“有理数”和“整式的加减”以及九年级下学期的最末第二章“锐角三角函数”是学生们点击频次最高的内容。而八年级上学期的“全等三角形”和“轴对称”,以及九年级下学期的最末一章“投影与视图”,则最少被问及。事实上,男女学生在共计12章的内容上,其答疑频次排序完全等同;特别地,在八年级上学期和九年级下学期,男女学生答疑频次排序的一致率分别达到60%和75%。在多数情况下,男女学生的位次差异仅为1个位次(14章)或2个位次(1章)。图1显示,男女学生在答疑频次排序上差异最大的是九年级上学期的“概率初步”内容。在男生序列中,该内容排在第21位,在女生序列中,其排在第26位1。这表明,“概率初步”于女生而言是一个相对简单的内容,而于男生而言是一个预期中等难度的内容。位次差异第二大的是七年级上学期的“几何图形初步”,这是初中第一个学期的最末一章内容,也是初中数学中首次涉及几何主题。男生在该篇章上的答疑频次位列11而女生位列14,也就是说这个内容的相对难度于男生而言要高一些。当然是否男生对几何图形有更大的学习情趣,以使他们的答疑频率有所提升,也是一个值得进一步探究的问题,尽管这已超出了本文的研究范围。
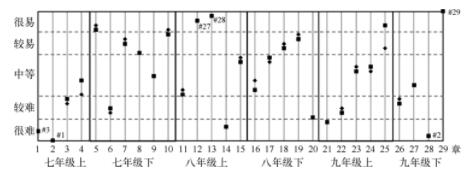
图1 男女学生在初中数学内容上的答疑频次排序(以章为分析单位)
注: ◆表示男生的频次排序,■表示女生的频次排序;#标注的是具体频次的位列,这里仅标出相对最难的3章(1—3)和相对最易的3章(27—29)。
根据线性回归系数βj的大小,本研究将初中三年数学的29章内容划分为“很难”“较难”“中等”“较易”“很易”等5个难度等级。如图1所示,除“中等”难度的篇章占所有篇章内容的三分之一,其余难度等级的篇章各占六分之一。不难理解,答疑频次位列前三的内容,其平均难度2等级皆为“很难”,末三位的内容则皆为“很易”。在答疑频次排序上出现最大差异的“概率初步”,其平均难度等级为“较易”,而位次差异第二大的“几何图形初步”为“中等”难度内容。
以上分析比较的是各章知识内容在男生群体和女生群体内部各自的相对难易水平。利用逐步回归法,AIC值最小取得22 929,其所对应的最优多元线性回归模型中,仅在5章内容上出现非零的交互效应值αj。事实上,在平均难度等级为“很难”与“中等”的全部14章内容上,男女学生的需求不存在明显差异。在“较难”的2章内容上,女生的需求明显要高于男生,分别为九年级上学期的“二次函数”(αj=-0.049)和九年级下学期的“反比例函数”(αj=-0.039)。在“较易”的2章内容上,男女学生的需求也出现了较大的差异,其中女生在八年级下学期的“平行四边形”(αj=-0.043)上有较高需求,而男生在九年级上学期的“概率初步”上较女生有更多的需求(αj=0.082)。在平均难度等级为“很易”的七年级下学期的“相交线与平行线”上,女生也显示出比男生明显更多的需求(αj=-0.067)。以章为单位的分析结果表明,女生相对男生对答疑的需求在总体上要更多一些。这与图1所显示的趋势是一致的,在近80%的知识内容上,男生组的频次相对位列要高于或等同于女生组。
在数学教学中,教学内容往往会按照知识的体系结构分类出若干篇章,而在每一章又会分为若干个小节。通常,章及其所含的节的内容在难度上大致会是在一个等级水平上,但也会存在一些差异。比如,八年级上学期的“轴对称”一章,其平均难度等级为“很易”,而其中的节“对称点、垂直平分线、对称轴、垂直平分线的性质”的平均难度等级则为“很难”。又如,同样是在八年级上学期,平均等级难度为“很难”的“整式的乘法与因式分解”一章中含有“中等”难度的节“分解因式、提公因式法、公式法”。因此,为更深入地了解学生在各个数学知识点上的学习情况,类似以章为单位的分析,同样也在节的层面上展开进行。
显然男女学生的答疑频次排序,在以节为单位比对时,其所显现出来的差异要远远大于以章为单位的比对。在所有83节的内容上,男女学生频次排序位次差异不超过4个位次的共有74节(零位差: 17节;1个位差: 29节;2个位差: 16节;3个位差: 6节;4个位差: 6节),占到总节数的88%左右。答疑频次排序差异最大的节内容是“解一元一次方程”,男生的位次为53,女生的则为63,表明这一内容于男生而言相对难度要更高一些(见图2,男女学生的群内相对难度相差一个等级)。频次排序差异第二大的有3节内容,分别是“与三角形有关的线段”(男生: 19;女生: 27)、“平行线及其判定”(男生: 27;女生: 19)和“平行线的性质”(男生: 59;女生: 51)。在“二次函数与一元二次方程”(男生: 29;女生: 22)和“用列举法求概率”(男生: 57;女生: 64),男女学生的频次位列差为7个位次。
图2 男女学生在初中数学内容上的答疑频次排序(以节为分析单位)
注: ◆表示男生的频次排序,■表示女生的频次排序;这里仅显示频次排序差异在3个位次及以上的节。
从图2可以看出,在八年级上学期的数学内容上,男女学生的答疑频次排序是最为接近的;在该学段的5章16节内容中,仅在4节内容上,男女学生的答疑频次排序出现较大的位差(25%)。差异相对集中的是在九年级下学期,在该学段的4章10节内容中,男女学生的频次排序出现较大的位差有4节内容(40%)。而且,其中的3节出现在同一章中,且该篇章只含有3节内容。另外,在七年级下学期,女生在多数的小节上,其相对答疑需求要明显高于男生。
本研究进一步通过逐步回归分析发现,在AIC值取得最小值288 088时产生的以节为单位的最优线性回归模型中,在总共83节中的13节内容上出现非零值的交互效应值αj,表明男女学生在约15%的内容上,他们的学习需求有明显的差异。具体来说,男生在7节内容上有明显更多的需求,2节来自“概率初步”,节的平均难度分别为“中等”和“较易”,2节来自难度等级最高的“圆”,这4节的内容都出现在九年级上学期。其余3节的内容,分别与七年级上学期的“一元一次方程”、七年级下学期的“二元一次方程”和八年级下学期的“数据的分析”有关,其难度等级为“较易”或“很易”。在这7节内容中,男女需求差异最大的是“弧长和扇形面积”(αj=0.125),其次是“解一元一次方程”(αj=0.121),差异最小的内容是“实际问题与二元一次方程组”(αj= 0.080), 次最小的是“用列举法求概率”(αj=0.086)。
有意思的是,所有的女生需求明显高于男生的节的难度等级至少为“中等”,其中包括1节“很难”的七年级上学期的有关“有理数”的内容,3节“中等”及“较难”的七年级下学期的有关“相交线与平行线”和“二元一次方程组”的内容,和2节“中等”及“较难”的九年级上学期学习的“二次函数”内容。在这些知识点中,差异最大的2节都是关于“相交线与平行线”的,即“平行线及其判定”(αj=-0.134, p<.05)和“平行线的性质”(αj=-0.105, p<.05),差异最小的是“三元一次方程组的解法”(αj=-0.091),次最小的是“正数与负数”(αj=-0.093)。
四、 研究结论与启示
本研究基于2 000名初中学生的在线答疑数据,根据他们对各项数学知识内容上在学习平台上的点击频次,探寻他们在初中阶段数学学习上的难点内容,并利用线性回归模型比较男女学生在这些知识难点内容上是否存在明显差异。分析显示,对于全体学生而言,“整式的加减”、“有理数”和“锐角三角函数”是点击量最大的3章;细化到节点,“正多边形”、“正数与负数”和“解直角三角形及其应用”则是学生们最多问及的知识内容。答疑频次相对最小的内容包括“全等三角形”、“轴对称”和“投影与视图”;在节点层面上,则是“平面直角坐标系”、“最短路径问题”、“位似”和“体质健康测试中的数据分析”等。在这些位列答疑频次序列首尾的章与节的分布上,男女学生各自的列表基本保持一致。这表明,对于初中学生而言,无论是男生还是女生,数与代数的知识较图形与几何知识都要更具挑战性。一方面,这与学生从初中阶段开始需从算术思维向代数思维转型不无关联,这是学生在数学学习中的一个共同的重大转折点,同时也是教师教学的一个关键性转折点。另一方面,这可能与图形和几何在课程标准中的要求有明显降低有关,而这部分内容在传统上是初中数学学习中的一个难点,如今已不再是难点了。课程标准要求难度上的这一调整是否矫枉过正,是很值得探索的。
虽然男女学生在初中数学知识学习的难点分布上,从总体来看表现出较高的一致性,尤其是在“较难”和“中等”难度等级的知识内容上。然而,在部分知识内容上,男女学生还是存在明显差异的。特别地,在以章为单位的分析中发现,女生在更多知识内容的学习上需要明显更多的帮助,包括代数类的“二次函数”以及几何类的“平行四边形”和“相交线与平行线”,而男生仅在概率学习上需要明显更多的帮助。在几何能力的差异上,赖莉、诺伊曼和安德鲁斯就曾指出这可能是认知能力上呈现出最大差异的一类[13],且此类差异随着年龄的增长有增大的趋势[14]。
以节为单位的分析显示,男生寻求明显更多帮助的知识内容大多处于“较易”和“中等”水平,包括方程和方程组的求解,以及概率问题等;而女生则对“中等”及以上难度等级上的知识内容有明显更多的帮助需求,包括二次函数以及与平行线有关的内容等。在难度等级最高的内容上,男女学生的需求也存在有明显差异,其中男生对圆知识的学习、女生对正负数知识的学习有明显更多的帮助需求。这些差异在多个其他研究中也有类似地出现,例如,海德、芬内马(Fennema)、赖安(Ryan)、弗罗斯特(Frost)和霍普(Hopp)就发现男生在复杂问题解决上较女生有更突出的表现。[23]
本研究的发现对于实际的课堂教学是有着积极的启发意义的。分析表明,初中数学的开篇知识内容,无论对于男生还是女生,都是一个较大的难点,因此,教师不仅需要在教学中给予充足的诠释,同时也要给正处在代数思维转型中的学生以更多的理解和帮助。当然,注册的初中学生用户大多是从初一年级开始参与到此学习平台上的活动的,这或许也在一定的程度上助力初一数学内容的点击量略高于其他两个年级内容的点击量。而在另一方面,系统的初中学生用户群的总量达到了2 000万的规模,这就大大地削弱了起始使用年级所带来的影响了。事实上,点击频次位列第2位的内容出现在九年级的下学期。
在大多数的初中数学知识上,虽然它们的难易程度对于男女学生差异并不明显,但在个别内容上所呈现出的帮助需求的差异很值得引起教师们的特别重视。例如,在概率内容的知识掌握上,男生就较女生需要更多的指导和帮助。而女生似乎在一些概念性知识的把握上有更为明显的需求,如几何图形的性质,包括平行线、角平分线和二次函数图象等。从总体上看,女生需要更多帮助的知识内容的难度等级要高于男生,这表明男生在基础性知识的学习上有更多的帮助需求,而对于那些较具挑战性的高难度等级的知识点,男生的把握能力要优于女生。这一结论也是与男女生在数学竞赛中的表现相一致。
此外,本研究在研究方法上也进行了有益的尝试。第一,利用网络在线平台采集大规模数据,以改善传统研究中个案或小样本在偶然性和代表性的局限性,从而使研究结论更具普适性。同时,本研究主要立足于模式探索,因此模式的验证是后续研究的一种重要的关注点,以更增强本研究结论的普适性。第二,使用多元线性回归模型,探索局部的不同群组之间的差异性。第三,将初中三年的数学学习情况作为一个整体进行研究,改变以往局限在某个年级或某个章节的知识内容上进行研究的传统做法,从而提升研究结果的宏观性和全局性。而在探索整体特征的同时,本研究的分析也兼顾了男女学生在个别知识内容上存在微观差异。
参考文献
[1] Grub,N.,Jahr,H.M.,Neumüller,J.& Field,S.Equity in Education Thematic Review:Finland Country Note[M].Paris:OECD,2005.
[2] Forgasz,H.& Rivera,F.Towards Equity in Mathematics Education:Gender,Culture,and Diversity[M].Berlin:Springer,2012.
[3] Burton,L.Gender and Mathematics:An International Perspective[M].London:Cassell,1990.
[4] Rogers,P.& Kaiser,G.Equity in Mathematics Education:Influences of Feminism and Culture[M].London:Routledge Falmer,1995.
[5] Grouws,D.Handbook of Research on Mathematics Teaching and Learning[M].New York:Macmillan,1992.
[6] Maccoby,E.& Jacklin,C.The Psychology of Sex Differences[M].Standard,CA:Standard University Press,1974.
[7] Wilder,G.Z.& Powell,K.Sex Differences in Test Performance:A Survey of the Literature[R].New York:College Entrance Examination Board,1989.
[8] Willingham,W.W.& Cole,N.S.Research on Gender Differences[A].Willingham,W.W.& Cole,N.S.Gender and Fair Assessment[C].Hillsdale,NJ:Lawrence Erlbaum Associates,1997:17-54.
[9] Friedman,L.Mathematics and the Gender Gap:A Meta-Analysis of Recent Studies on Sex Differences in Mathematical Tasks[J].Review of Educational Research,1989(2):158-213.
[10] Fennema,E.,Carpenter,T.P.,Jacobs,V.R.,Franke,M.L.& Levi,L.W.A Longitudinal Study of Gender Differences in Young Children's Mathematical Thinking[J].Educational Researcher,1998(5):6-11.
[11][17] Lindberg,S.M.,Hyde,J.S.,Petersen,J.L.& Linn,M.C.New Trends in Gender and Mathematics Performance:A Meta-Analysis[J].Psychological Bulletin,2010(6):1123-1135.
[12] Ganley,C.& Lubienski,S.T.Current Research on Gender Differences in Math[R].Reston,VA:National Council of Teachers of Mathematics,2016.
[13][21] Reilly,D.,Neumann,D.L.& Andrews,G.Gender Differences in Spatial Ability:Implications for STEM Education and Approaches to Reducing the Gender Gap for Parents and Educators[A].Khine,M.S.Visual-Spatial Ability in STEM:Transforming Research into Practice[C].Switzerland:Springer International,2016:195-224.
[14][22] Voyer,D.,Voyer,S.& Bryden,M.P.Magnitude of Sex Differences in Spatial Abilities:A Meta-Analysis and Consideration of Critical Variables[J].Psychological Bulletin,1995(2):250-270.
[15] Watt,H.M.G.Gender and Occupational Choice[A].Chrisler,J.C.& McCreary,D.R.Handbook of Gender Research in Psychology[M].New York:Springer,2010:379-400.
[16] Ellison,G.& Swanson,A.The Gender Gap in Secondary School Mathematics at High Achievement Levels:Evidence from the American Mathematics Competitions[J].Journal of Economic Perspectives,2010(2):109-128.
[18] Lubinski,S.T.,Robinson,J.P.,Crane,C.C.& Ganley,C.M.Girls' and Boys' Mathematics Achievement,Affect,and Experiences:Findings from ECLS-K[J].Journal for Research in Mathematics Education,2013(4):634-645.
[19] 郑静婉.中学生数学学习能力的性别差异教学研究[D].银川:宁夏大学,2011.
[20] 张奠宙.数学教育研究导引(第二版)[M].南京:江苏教育出版社,1998.
[23] Hyde,J.S.,Fennema,E.& Lamon,S.J.Gender Differences in Mathematics Performance:A Meta-Analysis[J].Psychological Bulletin,1990(2):139-155.
注释
1答疑频次位列越高,则表明学生在该数学内容上的答疑需求越低。
2平均难度等级,即考虑所有被试学生,与男生和女生群体内部的难度等级可能会略有不同。
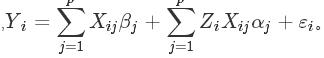 需要说明的是,Zi所表示的个体学生的性别,女生设为-1,男生设为1;协变量Xij表示第i个学习者是否在第j章或节上进行答疑,进行答疑设为1,否则设为0,因此X是29维或83维的一个向量矩阵;βj是第j个协变量Xij的效应值(可视为对应章或节的难易程度);αj是第j个协变量Xij与性别因素的交互效应值;p是总的章数(即29)或节数(即83);而εi是误差值,其分布服从正态分布N(0, σ2)。
需要说明的是,Zi所表示的个体学生的性别,女生设为-1,男生设为1;协变量Xij表示第i个学习者是否在第j章或节上进行答疑,进行答疑设为1,否则设为0,因此X是29维或83维的一个向量矩阵;βj是第j个协变量Xij的效应值(可视为对应章或节的难易程度);αj是第j个协变量Xij与性别因素的交互效应值;p是总的章数(即29)或节数(即83);而εi是误差值,其分布服从正态分布N(0, σ2)。