高中数学教学中波利亚思想的应用

　　摘    要：　以波利亚思想为指导思想, 将其运用于高中数学教学中, 实现了教学模式的转变, 以引促教, 激发学生自我感悟, 同时推广强化四步解题法, 使学生远离题海之苦。经过教学实践, 新模式教学方法能够激发学生数学学习兴趣, 培养提高学生的数学素养, 对高中数学教学具有一定的参考意义。

　　关键词：　高中数学教学; 波利亚思想; 教学实践;
 

　　一、波利亚思想是解决高中数学教育问题的重要方法与策略

　　乔治·波利亚是当代着名的数学家、教育家, 其在实变、复变函数、数论等领域做出了重要的开创性贡献, 而他对于数学教育的理论, 为后世的数学教学、学习开拓了新的领域。其对数学教育主要有三大贡献, 发展了数学解题的理论, 提出了要让学生、数学研究者进行合情推理的概念, 丰富完善了教育师资培训理论。这些对于高中数学的教育以及学生学习数学, 开拓视野, 培养数学素养具有举足轻重的意义。

　　高中数学是从九年制义务教育到大学教育的一个重要环节, 是培养学生数学意识, 启发学生数学思维的重要阶段。高中数学内容的宽度、深度和难度相比于初中数学都加深了许多, 一些初中数学好的学生, 到了高中会有所不适应, 而一些初中数学差的, 更容易放弃。同时, 受凯洛夫思想影响的精讲多练的教学方式, 很容易让学生和教师进入一种题海战术的圈中, 老师不布置题目, 总觉得不放心, 学生不多做题, 心里就没底, 看似解题速度提高了, 可是对于拓展类的题目却无从下手, 数学意识与思维还没有培养到位, 归纳演绎能力还欠缺。

　　二、实行以引促教的新模式, 让学生发现数学的精彩

　　(一) 完成预习表格, 培养学生自我发现知识的习惯

　　预习是老生常谈的话题, 但效果如何呢?过多地强调课堂讲解, 不重视思维的锻炼, 很容易养成学生被动接受的习惯。而预习是最好的让学生自己去接触数学的机会, 符合波利亚提出的让学生自我发现知识是最好的教育这一主张。在预习中, 要求每个学生在学习新的一节前, 将新的内容、应用范围、自己感悟、存在的难点完成一张表格, 如表1所示, 这样确保预习的内容落地, 形成一个具体实在的形式, 而不是以往的翻翻书而已。
 

　　(二) 不露声色推销知识点, 让学生自发接受知识

　　当然高中生的自习能力与分析能力还有所欠缺, 课堂仍是学习的主要环节。此环节教师宜采用启发性的教育, 不露痕迹地帮助学生。这就要求教师的观念要转变, 如推销员推销商品一样, 教师必须向学生推销知识, 让学生觉得知识是值得拥有的, 而不以教师的威严来强迫学生接受。

　　(三) 积极鼓励学生自我感悟, 让反思成为学生的自觉

　　在课堂上让学生积极互动、讨论, 让学生大胆地去分析、猜测, 让其实现顿悟:原来道理是这样的。打破学生只愿意听不愿意说, 以及只愿意问不愿意想的困局。也许有时学生不可能说出什么实质性的内容, 但是如果不断地强化这方面要求, 学生就会下意识地去想, 久而久之就会形成一种自觉, 这样不但培养了学习数学的自信, 也培养了教师与学生的感情。

　　三、强化四步解题法, 让学生学会自己出题

　　波利亚提出的四步解题法即先在脑中弄清问题, 草稿上写出解题计划, 进行科学的解答, 最后进行验算。在教学中强化四步解题法, 要求明确写出题目的要点、条件, 这样学生即使一下找不到思路, 也会去挖掘隐藏条件。解题后着重强调回顾这一个环节, 就是在做完题目后反思, 检查结果正确与否, 能不能再找到其它更快捷的方法, 这样就可以增强学生的思维, 同时培养严谨的作风。四步解题法促进了学生对于题型的理解和知识点的掌握, 打破了学生只愿意看不愿意动手计算, 只愿意答题, 不愿意再验算的困局。提高了学习效率, 远离了题海战术。

　　四、教学实践

　　(一) 实践对象

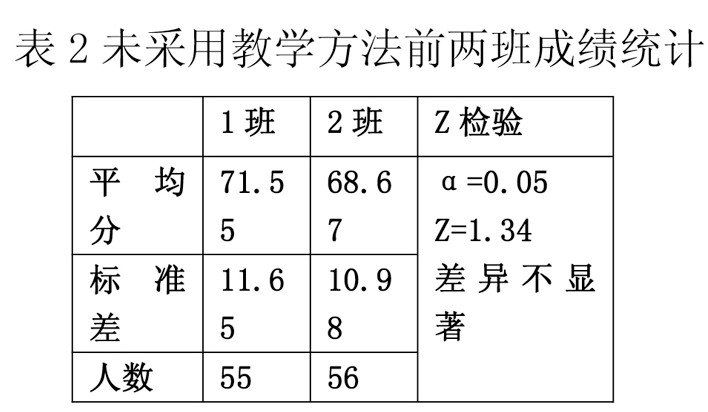
　　我校高一两个班。表2是对两个班的考试成绩统计, 通过z检验发现这两个班的成绩并无显着的区别, 排除了学习基础不同的影响。
 

　　(二) 实践方法

　　1班采用新的教学模式。

　　2班采用正常模式。课程结束后进行考试以及无记名投票。

　　(三) 实践结果:

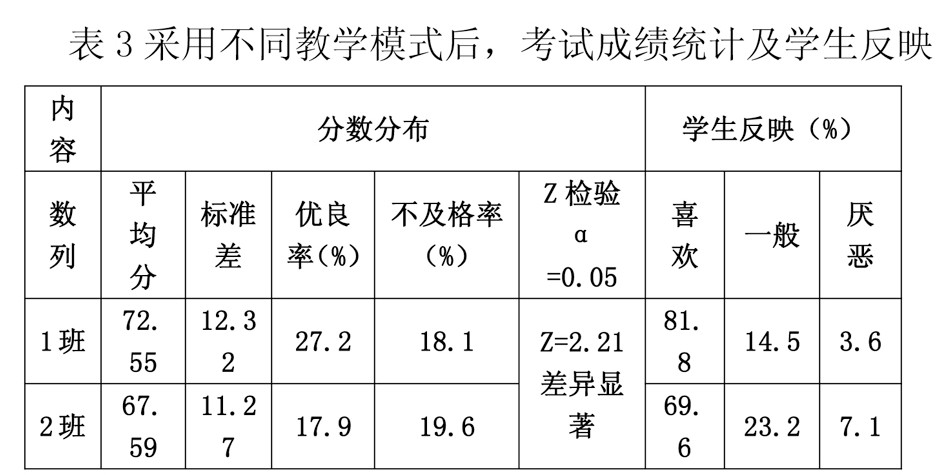
　　如表3所示, 1班的学生参与积极性比较高, 但是17%左右的学生由于基础稍差, 感觉有点吃力, 所以觉得这种方式不太容易接受, 但是其上课比以前活跃, 这类学生还需要进一步巩固。2班的积极性与前课程保持一样。分数中高分比例1班多些, 且平均分1班相对高些, 及格率高出些, 同时通过Z检验发现, 此次考试两班的分数已经不再是同一类分布, 证明此教学模式取得了一定的效果。

　　(四) 实践分析

　　数列部分是高中数学重要内容之一, 数列所涉及到的知识并不难, 但是学生们却普遍感觉数列的学习与解题比较棘手。这主要是出题者在出题的时候将一些重要的条件隐藏起来, 而四步解题法就要求学生将题目的全部条件找出来, 这样就让学生形成一种良好的分析题目的习惯, 从而能够在遇到较难的题目时能够积极地去寻找题中隐藏条件, 而不是手足无措。同时在学习数列的基本知识的时候, 先让学生们预习数列内容, 让他们寻找日常生活中数列例子, 让学生不再觉得数列抽象, 同时课堂上采取引导为主的教学模式, 让他们自己设计自己喜欢的数列, 并要求说出这些数列的特点, 同时让学生自己出数列的题目和小组学生互相交流。

　　不足之处, 新模式所花费的时间与精力较多, 1班课程进度比2班要慢。同时新模式的方法, 容易造成两极分化, 一些学生如果不能接受新方式, 则很容易丧失信心, 从而产生畏惧感, 就像总有人搀扶着, 突然一下子要自己走了, 很容易摔倒。但是, 从长远来看, 此类方法对于培养自主学习有很大的好处。

　　五、结论

　　本文以波利亚思想为指导, 结合数学教育形成了以引促教的新教学模式, 强化课前预习, 课堂上激励学生自我感悟。同时, 推广强化四步解题法, 让学生远离题海战术, 培养提高学生的数学素养。通过教学实践发现此方法取得了初步的成效, 当然在实践中还存在着一些不足, 下一步要注意区别不同的对象, 将教学模式更加细化, 争取让波利亚思想在数学教育中发挥更大的作用。

　　参考文献：

　　[1]魏珂, 胡典顺.基于“数学核心素养”视角下的解题教学——从波利亚解题思想出发[J].中学数学, 2017, (08) :95.
　　[2]崔恒刘.把精彩让给学生——用波利亚思想指导学生对一道路径题的探究历程[J].中学数学, 2013, (22) :7.
　　[3]崔恒刘.用波利亚思想教学生解题案例及反思[J].中学数学, 2017, (18) :93.