作为课堂教学的一个重要环节,有效的情境是优化数学课堂教学的一个重要方面。《普通高中数学课程标准(实验)》明确提出“教师要创设适当的问题情境,鼓励学生发现数学的规律和问题解决的途径,使他们经历知识形成的过程。”
由于数学高度的抽象性和概括性,学生难以理解,容易出现厌学情绪,有效问题情境的创设,可以帮助学生理解知识和方法,激发学生的学习兴趣,引发学生的认知冲突,使学生产生学习新知识的欲望。但在实际教学中存在着很多创设情境低效和无效的现象,诸如,情境拖沓冗长、平淡无趣、离题较远、花哨不实、晦涩难懂等。
那么,如何提高情境创设的有效性,本文结合教学实践,谈谈笔者的一些看法。
一、有效的问题情境
问题情境的有效性是指遵循教育学和心理学的客观规律,既要有良好的数学思维材料,又要渗透一定的情意活动,课堂实施中能够激发学生的情感、情意活动过程与认知活动过程交互作用,以尽可能少的时间、精力和物力的投入,取得尽可能多的学习效果,从而实现特定的学习目标,满足社会和个人的教育价值需求。
有效情境创设应该遵循以下基本原则:
1. 问题情境的情感性;2. 问题情境与教学内容的适宜性;3. 情境设置体现数学的思维性;4. 情境设置要符合学生的认知规律;5. 问题情境的简约性;6. 创设情境要恰当地运用教材。
二、有效问题情境创设的策略
(一)短
短,指的是所创设的问题情境在教学中使用时要尽可能的短。一节课 45 分钟,教学时间比较短,大部分时间应该放在重点、难点内容的研究、学生的反馈和知识巩固与训练上。而在实际教学中,一些教师用了较长的时间引入新课,浪费了教学时间,以致重点不突出、难点未突破,学生活动未展开,缺少必要的练习,前重后轻,连总结都没有就草草收场,这样的课是低效甚至无效的。所以笔者认为,情境的创设要讲究一个“短”字,为后续的学习活动留出充裕的时间。
案例 1.一位教师在讲授《指数函数的图象和性质》时,为了引出函数 y=2^x和 y=(1/2)^x,创设了如下两个问题情境:
(1)一个细胞分裂,由一个分裂为两个,两个分裂为四个,……,依此分裂下去,那么分裂次数与细胞个数之间的函数关系为 ____________.
(2)《庄子·天下篇》有这样一句话:一尺之棰,日取其半,而万事不竭。请写出一个函数关系式来表示这句话。
评析:这样的问题情境创设存在两个问题:一是学生在对问题的理解上存在障碍,需要较长时间的思考;二是两个问题比较多,需要学生分别求解,也需要较长的时间。有的教师为了帮助学生理解,用动画演示,就更浪费时间了,影响后续的学习。
因此,笔者进行了如下改进:
请同学们拿出一张纸,设纸的厚度和面积都为1,现在请同学们对折,观察和思考如下问题:
1.对折一次、两次、三次,纸的厚度和面积分别是多少?
2.如果对折 x 次,纸的厚度和面积分别是多少?
请两名学生上黑板上写,分别得到函数 y=2^x和 y=(1/2)^x,由此非常自然、简洁的引出指数函数的概念。原来是两个问题,现在只有一个问题,比原来的设计要减少一倍的教学时间。学生动手做、动脑想,亲身体验,也增加了学习情趣和参与度。
(二)平
平,指的是问题的难度要比较容易,不能过于繁难,否则,不但浪费大量的教学时间,而且会使学生对新课的学习失去兴趣和信心,出现烦躁的情绪。
案例 2. 一位教师在讲授《均值不等式》时,为了引出均值不等式,创设了如下的问题情境:
你去金店购买 10g 黄金,售货员用一杆两边臂长不相等的天平来称黄金,售货员先将 5g 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将 5g 的砝码放入右盘,将另一份黄金放于左盘使之平衡后再给顾客,按照这种称量方式,你有没有占到便宜呢?
解:由于天平的两臂不相等,故可设天平左臂长为 a,右臂长为 b(不妨设 a>b),先称得的黄金的实际质量为m1,后称得的黄金的实际质量为 m2.由杠杆的平衡原理:bm1=5a;am2=5b,解得 m1=5a/b,m2=5b/a;m1+m2-10=5a/b+5b/a-10=5a^2+5b^2-10ab/ab=5(a-b)^2/ab;∵a≠b;∴m1+m2-10>0,m1+m2>10,即 m1+m2>10所以你占了便宜。
评析:这个问题情境虽然和实际生活有一定的联系,但题目情境学生陌生,问题当中涉及到四个未知量,学生不会运用杠杆原理,又涉及到比较大小问题,所以问题过于繁难,问题的求解过程过于繁琐,学生一开始就陷入无所适从的境地,学生讨论也毫无结果,没办法只好老师讲解,待老师讲完已经过了15 分钟,学生已经感到厌倦,失去了情境设置的意义,并且严重耽误了重点内容的学习,不能完成本节课的教学任务。
因此,笔者进行了如下改进:
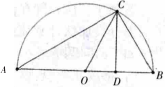
如图,在半圆 O 中,设 AD=a,DB=b,过 D 点作CD⊥AB,试比较a+b2和 ab姨的大小.
学生容易求得 CD=姨ab,因为 CD≤OC,所以a+b2≥ 姨ab,当且仅当 a=b 时,取等号.
此问题学生比较熟悉,求解过程也相对容易,既很快引出了均值不等式,又给出了均值不等式的几何解释,起到了一箭双雕的作用。
(三)趣
趣,指的是问题情境要生动有趣,激发学生的学习兴趣和求知欲望。顾泠沅先生认为,认知结构和情意状态是互相促进的两个方面,激发学生的动机、兴趣和追求的意向,加强教师与学生感情交流,是促进认知发展的支柱和动力。
案例 3.一位教师在讲授《数学归纳法》时,为了引出数学归纳法,创设了如下的问题情境:
费马(Fermat)是 17 世纪法国着名的数学家,他曾认为,当 n∈N 时,22n+1 一定都是质数,这是他对n=0,1,2,3,4 作了验证后得到的。后来,18 世纪伟大的瑞士科学家欧拉(Euler) 却证明了 225+1=4 294967 297=6 700 417×641,从而否定了费马的推测。
没想到当 n=5 时这一结论便不成立。
评析:这个问题情境虽然从数学史的角度设置,但只是一个单纯的数学问题,并且教师直接告知结论,缺少学生的参与,不能激发学生学习的兴趣,也不能使学生产生认知冲突。
因此,笔者进行了如下改进:
(1)邻居家有四个女孩儿,老大叫大妹,老二叫二妹,老三叫三妹,请你猜一猜老四叫什么?
(2)已知 an=n2-5n+5(n∈N*),可以求得 a1=a2=a3=1.
由此得到结论:an=1. 请问这个结论正确吗?
对于问题(1)学生感到非常有趣,跃跃欲试,说出了各种答案,当我说出了我的答案:满桌子。学生会心地笑起来:四个女孩儿正好一桌,从而调动起了学生的情绪。接下来问题(2)需要学生的理性思考,产生了认知冲突。笔者接着问:通过以上两个问题的分析你能得到什么结论?这样水到渠成地引出数学归纳法。
(四)实
实,是指问题情境的创设要紧扣课题,紧紧围绕教学内容和学习目标设计,不能为了创设情境而创设情境,不出现“多了花哨,少了实效”的现象。
案例 4.一位教师在讲授《基本计数原理》时,为了引出分类加法计数原理和分步乘法计数原理,创设了如下的问题情境:
(1)播放儿歌《数鸭子》片段。歌词:门前大桥下游过一群鸭,快来快来数一数,二四六七八,哎呀哎呀真呀真多呀,数不清到底多少鸭,数不清到底多少鸭!
(2)某市选择个性化车牌号的规则:
①第一位必须选择英文字母,后四位中必须任选一位为英文字母,其余三位为阿拉伯数字;②英文字母不得选用 I、O、Q。
这样的个性化牌号的容量是多少?
评析:本节课的学习内容是分类加法计数原理和分步乘法计数原理,而(1)中儿歌《数鸭子》的歌词与此内容毫无关联;(2)虽然与分步乘法计数原理有一定的联系,但超出了学生目前的知识基础和认知能力,而无法解决,所以笔者认为这样的问题情境对于本课来讲是无效的。
因此,笔者进行了如下改进:
(1)小明从甲地出发,去乙地,可以乘快客、火车和轮船,其中快客每日 6 班,火车每日 4 班,轮船每日 3 班,那么一天中小明有多少种不同的走法?
(2)小明从甲出发,路经乙地去丙地,从甲地到乙地 3 条路可通,从乙地到丙地 4 条路可通,那么小明有多少种不同的走法?
此问题情境来源于学生的生活实际,紧扣本节课的学习重点内容分类加法计数原理和分步乘法计数原理,学生做起来容易,通过这两个问题也易于理解两个原理。
(五)新
新,指的是创设的情境应该新颖、别致、巧妙,充满智慧,不落俗套。
案例 5.一位教师在讲授《事件的独立性》时,为了引出相互独立事件,创设了如下的问题情境:
(1)两名同学投篮,甲同学投中的概率为 0.7,乙同学投中的概率为 0.8,则两名同学都投中的概率是多少?
(2)在口袋中有大小均匀的 5 个球,其中 3 个红球,2 个白球,每次取一个,有放回地取两次,求在已知第一次取到红球的条件下,第二次取到红球的概率。
评析:在研究概率问题中,掷骰子、摸球、投篮、射击等问题情境屡见不鲜,不能引发学生的好奇心,不能调动起学生学习的积极性。对于我们课堂教学来讲,很多老师都采用这样的引入方式,问题陈旧,毫无新意。
因此,笔者进行了如下改进:
我们常说:三个臭皮匠,顶个诸葛亮,这句话对吗?今天我们从数学的角度来验证一下。已知诸葛亮能解决某个问题的概率为 0.85,三个皮匠解决此问题的概率分别为 0.4、0.5 和 0.6,试比较皮匠团队与诸葛亮解决该问题概率的大小。
此问题情境以俗语“三个臭皮匠,顶个诸葛亮”为背景,具有一定的人文色彩,并且提出用数学的方法加以验证,体现数学的应用价值,与本课的内容紧密相关,比较新颖,富有内涵,能够引发学生的好奇心和探究欲望。
余文森教授认为“情境之于知识,犹如汤之于盐,盐要融入汤中才能被吸收,知识也要融入情境之中,才能显示出活力和美感,才能被学生理解、消化、吸收。”
那么如何把情境这碗汤做得有滋有味,需要教师运用智慧,不断思考、积累、沉淀、创新,让学生感受到数学的魅力和数学学习的乐趣,使学生乐学、学会、会学,从而夯实数学基础、提升数学能力、提高数学素养。
参考文献:
[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
[2]余建国.提高问题情境的有效性的实践与思考[J].中国数学教育(高中版),2011,(12),12~15.
[3]王海波.浅析高中数学教学中的情境创设[J].中国数学教育(高中版),2011,(10),18~19.
[4]余文森.有效教学十讲[M].上海:华东师范大学出版社,2009.