2.6 软物质静电相互作用理论
库仑相互作用在软物质体系的研究中起着至关重要的作用。 这是因为大量的软物质、生物物理系统都处于极性溶剂(比如水)中。 由于溶剂极性分子和溶质表面电荷的相互作用, 往往会导致电离现象, 即表面的离子集团被溶解并带离表面, 从而导致溶质表面带电。 被溶解的离子集团和容液中的盐一起组成离子溶液, 并屏蔽溶质之间的库仑相互作用。 由于离子、带电离子、溶剂分子之间的相互作用的复杂性, 电解液中的带电表面的相互作用往往是非常复杂的。 例如, DNA, RNA 等生物大分子利用静电相互作用调控它们的结构和功能。 还有, 作为细胞外壳的生物膜含有很多带电的磷脂分子, 静电相互作用会影响细胞膜的结构和功能; 静电相互作用也在离子通道等其他生物系统中起着至关重要的作用。
在讨论库仑多体系统的理论方法之前, 我们首先需要讨论相关的物理模型, 即电解液模型和带电表面的模型等。 在电解液的原始模型 (primitivemodel) 中, 离子被认为是中心带电的硬球, 而溶液被认为是均匀的电介质。 在显式溶剂模型中, 水或溶剂的分子也需要和离子一起被显式地研究。 显式溶剂模型的研究对数值计算的要求很高, 一般仅局限于很小的系统和分子动力学的方法。 相对而言,原始模型对计算资源的要求比较低, 并可以用先进的蒙特卡罗方法加速。 不管用那一类模型, 长程相互作用的计算仍然是理论分析、数值模拟中的一个难题。
软物质中的库仑多体系统的理论研究方法主要有解析、数值两大类。 在解析理论方面, 最基本的是平均场理论, 即经典的泊松-玻尔兹曼理论(PB)。此理论将所有的离子近似为点电荷, 并忽略电荷之间的所有关联效应。 由此得出的非线性泊松 -玻尔兹曼方程(PB方程)的形式为
此方程在一些简单的几何条件下有解析解[67,68],在一般几何条件下只能用数值解方法求解。 PB 理论在低表面电荷密度、单价离子的情况下一般是比较精确的。 对于表面电荷密度高或有高价离子的系统, 离子之间的关联效应比较重要, 因此平均场理论不再适用。 比如, 大量的实验发现, 在一些系统总会出现电荷反转、通电吸引等奇异行为。 理论、数值研究显示在强带电表面附近的电荷关联效应可能会有电荷反转的现象。 但是, 理论预言的表面电荷密度大大超出了实验系统的数值[69].
下面各种理论方法可以考虑关联效应: 1) 场论的方法可以抓住长程的库仑关联, 但是无法正确处理短程的离子硬核细节[70]; 2) 自洽场方程 (self-consistent ?eld theory approximation), 也无法正确处理离子的硬核细节[71]; 3)对二维系统, 有基于Grassman 反对称代数方法的严格解, 但是此方法无法适用于三维系统; 4) 各种修正 PB 方程[72]、重整化 PB 理论[73]等。 这些方法的任意性比较大, 其效果往往依赖于我们对系统的多体关联的正确理解。 所有这些方法各有优缺点, 目前没有一种办法是被普遍接受的。 另外, 还有一些系统呈现出特殊离子效应 (ion specic effects), 这样的系统无法用原始模型描述[74]. 换言之, 我们必须用显式溶剂模型和更加微观的带电表面模型。 目前对特殊离子效应的理解不够深入, 缺乏一般的理论。
库仑多体系统的数值理论方法主要有下面三类: 蒙特卡罗模拟方法、分子动力学模拟方法、密度泛函方法。 相对于另外两种模拟方法, 密度泛函方法[75]的计算量较小, 但因其需要做一些难以控制的近似, 精度往往无法保障 (泊松-玻尔兹曼方程和自洽场方程也有数值解的各种方法, 在这里我们不分别讨论)。 由于库仑作用的长程性质, 边界条件的处理是一个关键的问题。 一般的处理方式是用周期边条件, 并用 Ewald 求和的办法将长程的部分势能/力场变换到傅里叶空间计算。 由此所得的方法计算复杂性为N3/2(即计算一个自由度为N的系统的总能量需要N3/2的计算量)。 用快速傅里叶方法, 可以将速度进一步提高到Nlog(N)[76]. 我们也可以用多尺度模拟的思想[77,78], 模拟一个球形区域内的系统, 并用泊松 -玻尔兹曼理论和镜像电荷的方法处理外面的区域。 这样所得到的模拟方法可以避免周期边条件带来的人为误差。 另一种快速计算能量的方法是利用实空间的多极矩展开, 即所谓的快速多极算法[79], 复杂度为N, 或树算法 (tree code), 复杂度为Nlog(N)。 最后, 可以利用 GPU(图形处理器) 的大规模硬件并行计算能力开发高效的并行算法。 由此得到的模拟方法可以在
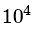
级别的系统模拟上得到比其他方法更高的速度。
2.7 自组织现象
在软物质体系中有一种独特的现象即自组织现象。 正如引言所述, 软物质体系的一个重要特征是多自由度, 对应于相空间的多维度特征。 从而使得体系具有较大的构型熵。 这时即使在室温下, 熵自身对自由能的贡献就有可能超过相互作用内能成为主要因素, 驱动整个体系演化。 在这个过程中系统的总熵是增加的, 但是多个自由度之间有可能互相竞争, 在某个自由度上出现熵减的行为, 从而“析出”某种对应的序和结构, 这就是熵驱动的自组织现象。 一个纯粹由相互作用决定的结构变化过程是不能称为自组织过程的。
3 前沿问题以及未来重点发展的方向
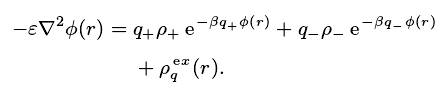
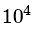 级别的系统模拟上得到比其他方法更高的速度。
级别的系统模拟上得到比其他方法更高的速度。