3.1 液晶弹性体
近年来, 液晶弹性体作为智能材料已成为多学科交叉的热点研究方向, 例如利用液晶弹性体的特殊性能设计具有微量液体传输功能的器件, 可实现贵重液体的无损输送; 通过在太空设备上构筑光响应性推进器, 可直接将太阳能转化为机械能供设备长期运行。 液晶弹性体对外界刺激的敏感响应可用于开发防伪技术, 由于在外界刺激下液晶弹性体可引起定量的弯曲、收缩、膨胀或者表面图案的精确变化, 有极高的辨识度, 并且不易被模仿 (俞燕蕾,液晶弹性体: 性能与形变)。
3.2 高分子理论和模拟
近年来伴随着高分子物理实验的发展, 以及进入 21 世纪以来大规模计算技术的发展, 高分子物理理论发展迅速。 结合高性能计算机和计算技术的发展, 理论计算和模拟已发展成为独立的高分子科学研究手段, 在高分子材料优化设计和性能与结构间的关系研究中取得了令人瞩目的成功, 同时在高分子物理中发展的理论模拟方法, 也可以应用到软物质物理的其他领域。
借助近代理论物理发展起来的新方法, 近代高分子理论计算与模拟结合高性能计算以解决高分子领域中的科学问题。 过去的大多理论模拟方法主要还是用来解决小扰动下的平衡态附近的性质,或者是对外界的线性响应问题, 远离这一近似下的很多问题却没能解决, 例如平衡态之间的动力学路径问题, 对大扰动过程的描述, 非线性的结构和性能的关系, 有限尺寸下的受限相行为等。 要解决这些问题, 还需要发展新的理论和数值计算与模拟方法。 当前研究的目的包括两个方面: 其一, 解决高分子凝聚态理论发展过程中所遇到的难题, 其主要特征是非微扰、非平衡、非线性, 这些理论上的难题包括超越高斯链模型的场论方法, 超越平均场方法, 带电高分子体系中的电荷关联效应, 高分子结晶、玻璃化转变中的相变、动力学问题等, 特别是结晶和玻璃化转变问题, 始终存在着很大的争议; 其二, 发展现有的高分子理论方法, 解决实际科学问题, 建立可测宏观量与高分子链构象及聚集态结构间的定量关系, 这方面的问题包括嵌段共聚物纳米印刷术 (大尺度上的可控自组装), 高分子体系的多尺度连贯研究, 聚电解质体系中的电荷关联效应,高分子流变学, 共轭高分子的光电性能等。
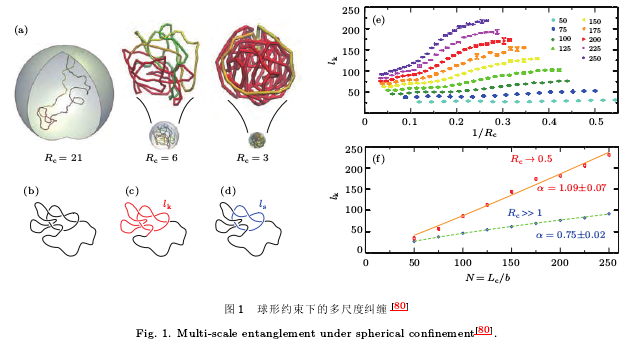
2011 年, Tubiana 等[80]对受限于钢性球壳内部的环形聚合物的多尺度纠缠进行了研究, 他们利用数值模拟的方法对几何约束下半柔性打结的环形聚合物链之间的相互作用进行了深入的探讨, 找到了描述几何约束的球壳半径和描述拓扑纠缠的打结长度以及环长度之间的标度关系, 显示了局部和整体的多尺度纠缠规律 (图 1 )。 整体和局部拓扑纠缠之间的关系是聚合物物理的重要研究内容,在生物学领域这种拓扑纠缠与真核细胞、细菌和病毒的基因组方面的关联是一个热议 的 话 题 [81-87];环状聚合物如DNA 在溶液中的结构[88]、缠绕动力学行为[89]、在纳米空洞中的行为也是最近研究的热点。
3.3 聚合物刷的自洽场和标度理论
早期, Zhulina 和 Vilgis[90]已经用标度理论对梳状和星形的聚合物刷做了大量的研究。 他们预测到星形聚合物刷高度具有和线性聚合物刷一样的标度规律。 Kroger 等[91]用平均场理论分析了多分枝聚合物刷的标度性质。 最近通过分子动力学研究, Merlitz等[92]发现基于Alexandre-de Gennes模型基础上的标度理论, 仍然适用于星形聚合物刷, 并且证实了 Polotsky 等[93]通过自洽场预测的多分枝刷的两种分支状态, 一种被强拉伸, 一种收缩在刷子体系内, 模拟还发现这两种状态不仅存在而且还可以相互转换, 这种转化会提供多分枝聚合物刷的拉伸等力学或应该存在能量壁垒等信息[94].这种能量壁垒的存在提供了利用多分枝聚合物刷的这两个状态设计高效转换开关的可能性和应用空间, 况且还可以利用溶剂等调控手段[95]. 人们有理由相信这些特性会由于多分枝聚合物链结构的拓扑结构特征 (分叉数目增加)增加而强化。 这是一个有趣而且应该研究的内容, 而且随着构成聚合物刷的聚合物链的拓扑复杂程度的增加, 聚合物刷的一些新特性将会显现出来。