摘 要:教学实践表明,课堂教学的有效性离不开教师的引导,教师引导的有效性决定于教师的专业水平。根据初中数学概念教学的地位和特点,结合 PCK 内涵的四个组成部分进行数学概念的 PCK 内涵解析,能帮助教师深刻理解概念本质、认识概念教学的学科教育价值,能够理解学生的经验与困难,可以进一步阐释概念的本质属性,发展学生的数学素养,设计恰当的教学策略,可以提升概念教学的有效性。
关键词:初中数学概念教学;PCK 内涵解析;数学概念 PCK 内涵。
一、初中数学概念教学的意义及一般方法。
(一)初中数学概念教学的意义。
概念是事物本质属性在人脑中的反映,是思维的基本形式之一,是进行判断和推理的基础。数学概念是反映数学对象本质属性的思维形式,是形成数学知识体系的基础,是数学思想方法的重要载体。而数学概念教学的意义不仅在于让学生掌握数学概念本身,更重要的是在获得概念本质属性的过程中,通过观察、比较、分析、归纳、抽象、概括等数学活动,发展学生的推理能力、抽象思维,体会数学的思想方法,促进学生的数学学科素养的发展。因此,数学概念的教学对数学学科和学生发展都有重要的意义。
(二)初中数学概念教学的一般方法。
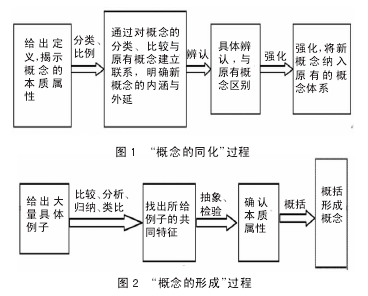
在初中数学课程中,概念众多,南京师范学院的章飞教授就概念教学实施的角度,将概念分成 3 类(对象性概念、度量性概念、观念性概念),其中的对象性概念是教学的重点之一。对象即数学的研究对象,如各种数、各种式、各种图形的概念。概念教学的过程一般要经历:一是概念的引入(揭示研究的必要性);二是概念的获得(揭示概念本质属性的过程);三是概念的巩固与运用(了解概念的运用,在运用中进一步理解、巩固概念)三个过程。其中概念的获得最重要,它主要有两种基本形式---概念的同化和概念的形成(具体见图 1、图 2)。
从图中可以看出,“概念的同化”是直接明晰概念,通过教师的讲解、解释,学生逐步明确概念的内涵;通过运用变式的材料和例证,学生明确概念的外延。“概念的形成”是经历对具体特殊实例的特征的归纳、类比,检验后明确概念的本质属性;给出定义并用常用的形式符号表示概念。这就要求学生经历一个对概念本质属性的抽象过程,在此过程中发展学生的抽象思维、推理能力、符号意识、模型思想等,并使学生逐步形成数学的学科观念。
可见,不管采用哪种方式,教师都必须准确、深刻地理解概念的本质属性,了解概念的内涵外延,有清晰、完整的概念结构体系。同时,要了解不同概念适用哪种概念获得的方式。这就依靠教师对概念本身的理解,并设计出有效的概念教学策略。如果教师对概念本质属性的理解有偏差,对概念体系的认识不完整,对概念承载的数学教育价值不明确,那么,不论采取了怎样的课堂模式和教学策略,都不能够达成概念教学应有的目标,也就不能体现概念教学的意义。
二、进行初中数学概念 PCK 内涵解析的作用。
(一)运用 PCK 内涵解析进行概念教学可以进一步阐释概念的本质属性。
经过十多年的新课程改革实验,《义务教育数学课程标准(2011 年版)》倡导的教学理念已经逐步转化为教学行为,在概念教学中,教师一般都能让学生经历概念形成的过程,很少出现“一个定义、几项注意”的概念教学方式。但是,在“引导学生探究概念本质属性”的过程中,却屡屡出现对本质属性理解不准确的问题。尤其是,初中数学教材中很多概念的定义是用“形式化定义”或“发生式定义”方式给出的,其定义并没有揭示了概念的本质属性。在这些概念的教学中,教师就更容易出现将“形式化定义”作为概念本质属性的现象,在课堂上反复进行针对定义的辨析,而忽略引导学生体会概念所蕴含的丰富的问题情境、思想方法,使概念教学缺少了应有的教育价值。这样,既不能使学生深刻理解概念,也不能通过概念教学的过程发展学生的数学能力。例如,在“方程概念”的教学中,有些教师认为“方程”概念的本质属性是“含有未知数的等式”,由此可见,在课堂上让学生大量进行“判定下列各式是不是方程”的训练,使方程概念的教学成为辨析形式化定义的刻板过程,不能体现方程概念的教育价值。其实“方程是刻画现实世界数量关系的有效模型”,其本质是:建立已知、未知之间的联系,并借助已知求量求出未知量,继而解决问题“.在方程概念的学习中,学生应经历”用方程刻画不同情境中的等量关系的过程“,抽象出”本质属性“,并体会”方程是刻画现实世界数量关系的重要模型“这一思想,以发展学生的抽象思维和模型思想,体现数学学科概念教学的价值。
(二)进行初中数学概念 PCK 内涵解析可以有效发展学生的数学素养。
正确理解概念的本质特征是教师进行数学概念教学的必要前提,是通过概念教学发展学生学科素养、体现概念教育价值的保证。那么,在概念教学中怎样才能避免出现以上问题,从而体现概念教学的价值呢?
如二次函数概念的学习,有利于发展学生”数学抽象“的核心素养,发展符号意识。抽象是数学最本质的特征之一,也是数学最基本的思想之一。在二次函数概念教学时,学生将经历从丰富的实际问题中建立出函数关系式,然后分析所得到的函数关系的特点,抽象出共性特征,从而建立二次函数的概念。在这个过程中,学生最主要的思维活动就是”抽象“,因此,合理设计二次函数概念的教学将有利于发展学生”数学抽象“的核心素养,同时在建立二次函数一般形式的过程中发展学生的符号意识。
再如,二次函数概念的教学,有利于发展学生”数学建模“的核心素养,体会数学应用的广泛性。二次函数在军事、体育、物理、心理、建筑等现实世界中都有广泛应用,是一种重要的”数学模型“.在二次函数概念的学习中,学生需要分析不同情境中变量关系与变化规律,建立变量之间的函数关系式,这个过程就是”建模“.
二次函数概念教学这一重要概念的教育价值还体现在”过程与方法“层面。对于学生而言,获得二次函数概念的过程是”从特殊到一般再到特殊“的认识事物的过程,而二次函数所刻画的问题的复杂性,更实现了学生研究函数问题经验与方法的进一步的积累与提升。
由引可见,对一个概念的”PCK 内涵“作透彻解析,可以帮助教师深入理解所教概念的本质,了解这一概念与其他内容的联系,获得概念教学目标中的知识技能目标。能够帮助教师理解数学内容蕴含的数学思想方法、使学生在学习该知识的过程中能够发展其数学素养、形成学科观念。