数学与生活论文第六篇:实际生活中小概率原理的运用
摘要:小概率原理是概率论中非常重要的一个概念,在实际生活中应用也非常广泛。从生活中的实例出发,介绍了小概率原理在日常生活、风险投资、保单设计、质量管理等方面的应用。通过讨论,使人们全面认识了小概率原理。
关键词:概率论; 小概率原理; 小样本认知偏差;
The Applications of Small Probability Principle
QIN Bingjie
Basic Department of Shanxi Pharmaceutical Vocational College
Abstract:The principle of small probability is a very important concept in probability theory.It is also widely used in real life.This paper introduces the application of small probability principle in daily life,venture capital,insurance policy design,quality management and so on.This paper,through several practical cases,introduces its application in the aspects of life and work.
0 引言
生活中我们通常习惯于关注发生可能性较大的事情,其中原因在于概率论源于对赌博问题研究,在这种问题里我们当然关心那些胜率较大的策略。相应地,在考察概率分布时,我们重点关注的也是这个分布的峰值,概率统计诸多理论就是在研究“峰值”,大数定律和中心极限定理都使得人们习惯于相信随机现象在大尺度下的稳定性,因此人们关注大概率事件是有理论依据的。
但是我们在重视大概率事件的时候,也不能忽视小概率事件。我们工作和生活中就有一些事件,它们发生的可能性很小,但一旦发生危害却非常大。比如2011年温州动车相撞事件、2015年长江游轮倾覆事件、2017年九寨沟的地震事件等,这些事件发生概率很小,危害却很大,因此不能忽视,对这些问题的研究也非常必要。
1 小概率事件的概念及小概率原理
1.1 小概率事件的概念
我们知道,自驾出行有可能出交通事故,坐飞机可能遭遇失联,可为什么我们没有裹足不前,还要出游呢?我们知道,抓彩票可能中大奖,可为什么我们没有一哄而上、趋之若鹜呢?这是因为我们知道,这些事情发生的可能性太小了!
可能性也即概率,那么多小的概率算小呢?这个不能一概而论。比如某工厂生产一批灯管,不合格率是1%都可以出售,而医药企业生产的药品,不合格率是0.1%都不能出售,这是因为医药产品事关人类的生命健康,标准自然要高一些。
不过,在数学上,一般将发生概率小于0.05的事件称为小概率事件。
小概率事件还具有突发性和诱惑性两个特点,比如地震、海啸的发生等往往比较突然,而各种赌博游戏往往是利用丰厚的大奖来诱惑人们参与。
1.2 小概率原理
概率很小的事件在一次试验中几乎是不会发生的,这就是小概率原理;反之,如果事件发生了,有理由怀疑原假设是错误的,这也称为实际推断原理。
根据概率论中的伯努利(Jakob Bernoulli)大数定律,在试验条件不变的情况下,事件A发生的频率依概率收敛于事件A发生的概率,即在大量重复试验时,可以用事件A发生的频率来代替事件A发生的概率。这时如果事件A发生的概率很小,则在大量重复试验中它出现的频率也会很小。例如,假设事件A发生的概率P(A)=0.01,那么在100次试验中,大约只有1次出现A。
2 小概率原理在实际生活中的应用
2.1 在规避街头骗局方面的应用
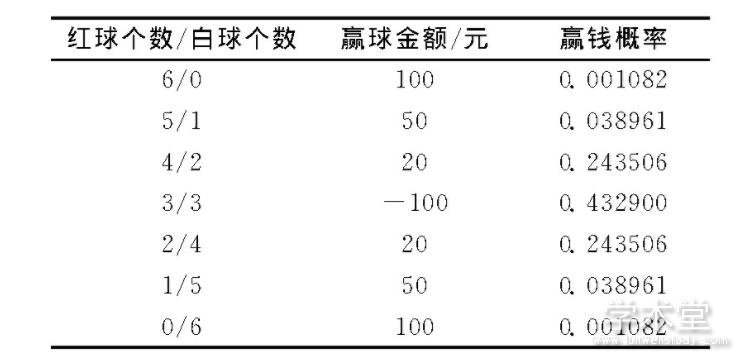
日常生活中,我们经常遭遇一些街头骗局,譬如下面的摸奖骗局。庄家在一个袋子里放6个红球和6个白球,这些球除了颜色不一样以外,其它完全一样。游戏规则为,每次任意从袋子中摸6个球,输赢规则如表所示。
这个规则看上去对顾客有利,因为7种情形只有一种是输钱的,其它6种情形你不用投资,均能赚钱。很多人禁不住诱惑,难免心动去试一试,但结局往往却是扫兴而归,输的钱从几十到几百不等。问题出在哪呢?我们不妨计算一下:
根据排列组合原理,任取6个球,取到i个红球和j个白球的概率可以这样计算:
由此可以算得各种情况输赢的概率如表所示。
可以看到,赢100元和赢50元对应概率都小于0.05,是小概率事件,在一次试验中几乎不可能发生,因此可以忽略。观察的重点是赢20元概率总计是0.487,而输100元概率是0.433,因此从平均下来输钱可能性更大。庄家就是利用小概率原理,设计使得赢钱的概率很小,因此赌的越多,输的就越多。
表摸球游戏规则及输赢概率
Table Rules and probability of winning or losing in touch ball game
2.2 在风险投资方面的应用
1994年成立的美国长期资本管理公司(LTCM),曾经是世界上着名的对冲基金。该基金聚集了一大批世界高智商精英,专门从事金融市场套利,是当时与量子基金、欧米伽基金、老虎基金齐名的国际四大“对冲基金”之一。
LTCM的投资模型是“不正常市场价差套利”。他们利用计算机追溯大量的历史交易数据,通过独特的算法,得出两种标之间“正常”的历史价差,如果现有价格与正常历史价差出现了“非理性”的偏差,计算机便随之建立标的组合,大举入市套利。
LTCM所遵循的就是“市场中性”原则,无多无空,主要以寻求标的效率落差形成的套利空间,并通过对冲化解市场风险。公司成立后的几年,这套交易模型取得了辉煌的交易成绩:3a间其资产净值从12.5亿美元上升到48亿美元,增长了2.84倍。
然而1998年这个巨人却轰然倒塌,公司一夜之间倒闭了,这是为什么呢?
其中一个主要因素是这一年出现了罕见的小概率事件!
1998年,由于国际油价下跌,导致国内经济下滑、政局不稳,俄罗斯政府不得不采取“非常”的举动,宣布卢布贬值,国债交易也随之停止。这一举动,导致国债市场出现空前极端的波动,叠加LTCM投资杠杆很高,短期内就产生了巨额损失,无力支撑,最终被监管机构接收。
LTCM案例给我们的启示是,历史数据和规律并不能等同未来,历史不会简单重复,市场环境的变化可能导致出现小概率事件,而这可能导致以前规律的失效。因此在投资中,对小概率事件的忽视可能导致极其严重的后果[1]。
2.3 在保单设计方面的应用
概率论是研究随机现象统计规律性的一门学科,而保险就是利用随机现象的统计规律性来化解风险的,保险与概率论密切相关,概率论是保险的数理基础。下面我们以一个保单设计案例看看概率论在其中的应用。
案例1:根据调查数据,某年龄段人的死亡概率为0.001。现有某保险公司要据此设计一份人寿保单,具体条款是:投保人每年缴纳300元保费,如果投保人当年死亡,保险公司负责赔付受益人10万元。现有1万人投保,问保单的设计合理吗?
分析:假设投保者1a内死亡人数为x人,则x~B(10000,0.001),公司一年的收入为1万×200=200万,赔付金额为10万×x=10x万元。若保险公司亏损,需200<10x,即x>20,即赔付人数大于20人。
投保人数n=10000数值很大,而死亡概率p=0.001数值很小,因此该分布可以用泊松分布近似,其中泊松分布的参数λ=np=10。
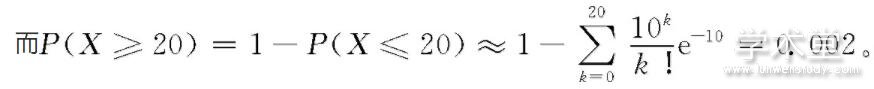
而这个值小于0.005,这意味着保险公司亏损是一个小概率事件,因此保单设计是合理的[2]。
2.4 在质量管理方面的应用
小概率原理在药物研发、疫苗接种、药品生产等方面都有广泛的应用。
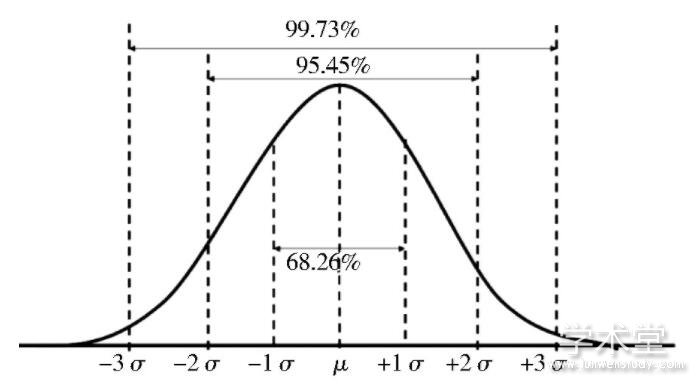
图1 正态分布的3σ准则
Fig.1 Normal distribution 3σcriteria
案例2:某个药品生产企业生产一种片剂,其质量服从正态分布,设质量为x mg,x~N(1000,202)。抽检时发现有某一片剂质量为1 080mg,问该药品能否通过质量检查?
解析:根据正态分布的3σ准则(图1),该片剂质量落在(μ-3σ,μ+3σ)区域的概率几乎为1,也就是落在(940,1060)内的概率几乎为1。但是现在抽检结果为1 080mg,并没有落在这个区域,这就说明发生了小概率事件。而小概率事件在一次试验中几乎是不可能发生的,现在发生了,就怀疑该批产品可能有问题,因此药品不能通过质量检测[3]。
3 如何正确理解小概率事件
对于小概率事件,人们通常会有两种极端反应。
一种极端反应是麻痹大意,把小概率事件等同于不可能事件。要注意,小概率事件并不是不可能事件。不可能事件是发生概率为0,是必然不会发生的事件,而小概率事件概率虽然小,在一次试验中发生的可能性也很小,但大量重复试验后,其发生的可能性却几乎是必然的。
可以证明:假设事件A发生的概率为p,n次试验中A不发生的概率为(1-p)n,发生的概率为1-(1-p)n。不管p的值多小,当n→∞时,事件A发生的概率为,即事件A发生的概率是必然的[4]。
生活中,我们也有很多谚语讲的是这样的道理,比如“瓦罐不离井边破,只怕来的遭数多”“常在河边走,哪能不湿鞋”等[5]。
另一种极端反应是过分放大。比如2011年的动车相撞事件,民间反应很大,甚至导致官方被动降低高铁速度;还比如有些人经常看车祸视频,心理产生阴影,对高速路出行产生了恐惧心理等。其实这些情况本质上是一种小样本认知偏差,即在夸大了小样本条件下事件的概率对总体概率的代表性,这也是不对的。
总之,小概率事件反映了生活中一类特殊而重要的现象。全面正确认识这类事件,既可以避免无谓的损失,又可以在矛盾时找到有利的取舍依据。我们应该认识和把握好这个工具,让它更有效地为我们服务。
参考文献
[1]吴传生.经济数学:概率论与数理统计[M].北京:高等教育出版社,2015.
[2]龙永红.概率论与数理统计[M].北京:高等教育出版社,2009.
[3]焦春义,燕远伟.“小概率事件”在医学应用中的模型探讨[J].科技资讯,2006(36):91-92.
[4]赵彦玲.小概率原理在实际生活中的应用[J].赤峰学院学报(自然科学版),2015,31(22):8-9.
[5]高祖新.医药应用概率统计[M].北京:科学出版社,2014.
点击查看>>数学与生活论文(精选论文8篇)其他文章
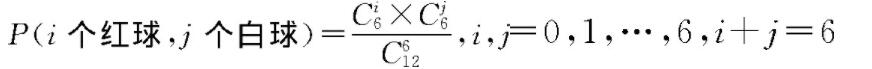

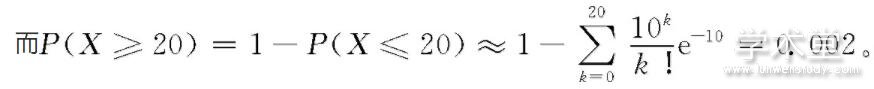 而这个值小于0.005,这意味着保险公司亏损是一个小概率事件,因此保单设计是合理的[2]。
而这个值小于0.005,这意味着保险公司亏损是一个小概率事件,因此保单设计是合理的[2]。