数学分析与概率论中的相互应用作用研究

　　摘要：数学分析与概率论是互相渗透与相互依存的关系，两者共同发展，互相影响。数学分析作为一门基础性的学科，经过多年的发展与研究已经形成了一套较为完备的理论体系，并且对概率论的发展起到了良好的促进作用。反之，概率论的计算方法以及解题思路也可以把一些复杂的数学分析问题进行简化，实现确定性问题与随机性问题之间的有效转化，使得数学分析问题得以高效解决。

　　关键词：数学分析； 概率论； 相互关系； 应用；

　　Abstract:Mathematical analysis and probability theory are interpenetrating and interdependent. The two develop together and influence each other. As a basic discipline,mathematical analysis has formed a relatively complete theoretical system after years of development and research,and has played a good role in promoting the development of probability theory. Conversely,the calculation method of probability theory and problem solving ideas can also simplify some complex mathematical analysis problems,realize the effective conversion between deterministic problems and random problems,and make the mathematical analysis problems efficiently solved.

　　Keyword:Mathematical analysis; Probability theory; Mutual relationship; Application;

　　1 数学分析在概率论中的应用作用

　　1.1 形成公理化体系

　　具有某种特殊性质或者结构的集合均属于数学分析的研究范围，集合论应运而生，并成为了数学公理化体系形成的基础[1].数学分析中经常应用两种积分，分别是黎曼积分与勒贝格积分。在处理具有良好性质的函数时使用黎曼积分可以发挥出良好的效果，但是如果遇到级数、多元函数或者积分与极限交换次序等复杂函数问题时，就会遇到较大的困难。后来，勒贝格积分的出现在集合论与测度论之间形成了有效联系，发现了概率和集合测度上某些相似性，为概率论的公理化体系形成奠定了基础[2].

　　1.2 傅立叶变换与特征函数

　　数学分析中常常使用的解题工具就是傅立叶变换，主要包括傅立叶积分和傅立叶级数等相关内容。将傅立叶变换引入到密度函数或者分布函数中即可得到"特征函数".数学分析中提到的定理为F1、F2作为两个具有界变差的函数，F是两者的卷积，g、g1、g2分别为F、F1、F2的傅立叶斯蒂尔吉斯变换，则可以得到如下等式：g（λ）=g1（λ）·g2（λ）[3],即两个独立随机变量和的特征函数是两个独立特征函数的积，使用公式表达则可以得到ФX+Y=ФX（t）·ФY（t），其中X和Y是两个彼此独立的随机变量，该方法的使用在很大程度上降低了随机变量函数的难度。

　　1.3 随机变量与分布函数

　　将数学分析运用到概率论中可以将很多问题进行简化。分布函数和随机变量是数学分析中涉及到的两个函数概念，分别代表了实函数和集函数。如果函数存在对应关系，则可以按集合和实数的顺序转换随机事件，最后将集合函数替换为实函数。另外，通过从函数的角度测量分布函数，可以找到函数的可积、可导和单调有界性质。该函数的特殊属性在许多数学问题的分析和计算中具有实际应用。

　　1.4 中心极限定理与大数定律

　　概率论主要研究的问题是中心极限定理与大数定律，它们也是数理统计中的理论基础。两者都涉及随机变量序列的极限，并且与数学分析中提到的序列极限和函数序列的极限具有极大的相似性和相关性。为此，将数学分析中相同数量级的方法可以应用于与中心极限定理和大数定律有关的问题。

　　2 概率论方法在数据分析中的应用

　　2.1 数学期望在不等式问题中的应用

　　概率论在数学分析中的应用是比较常见的，例如，如果使用传统的数学分析方法解决不等式问题，解题过程是相对复杂的，如果将数学期望引入到不等式解题过程中，则可以简化不等式的解题过程。数学期望主要有3个性质：第一，如果使用ζ描述随机变量，对于存在的Eζ2而言，可以获得不等式（Eζ）2≤Eζ2;第二，如果数学随机变量为ζ和η，则会存在Eζ2和Eη2,从而可以得到不等式[E（ζη）]2≤Eζ2·Eη2;第三，如果选择两个相互独立的随机变量ζ和η，存在EζH和Eη，则可以得到不等式2Eζ·Eη≤Eζ2·Eη2[4].

　　例如：区间[a,b]上两个函数f（x）与Ф（x）均为可积函数，Ф（x）>0,证明

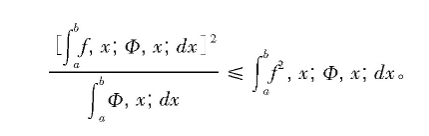
　　证明：如果随机变量ζ的概率密度函数是

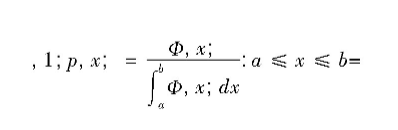
　　（2）p（x）=0,其他；

　　η=f（ζ）为随机变量ζ的函数，可以得到：

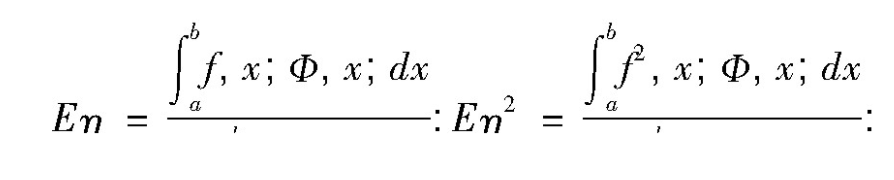
　　由不等式（Eζ）2≤Eζ2可得结果：

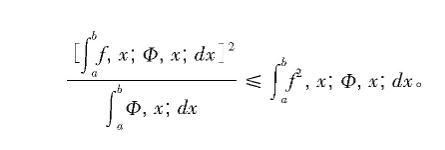
　　2.2 中心极限定理在数学分析中的应用

　　如果直接使用数学分析的方法去解决一些相对复杂的极限问题，通常情况下是很难快速进行求解的。而运用概率论中的中心极限定理，就可以使复杂的极限问题变得容易解决[5].中心极限定理加强了概率论与数学分析的联系，在数学分析中进行极限值求解时，如果t>0,可以对随机变量进行设定，例如ζ1、ζ2、ζ3……ζn.以上变量均服从p（t）函数。在中心极限定理下，可对t的值进行分区限制，即t=1,t>1,0<t<1,可将极限求值问题进行简化，快速的完成求解。

　　2.3 随机变量函数在数学分析积分中的应用

　　数学分析中，经常用"分割"、"近似求和"、"取极限值"法求解不规则图形的面积、物体体积以及弧长等。概率论中连续型的随机变量。具有分布律、分布函数以及概率密度等基本概念。分布律和分布函数是"求和"的关系，公式表示为F（x）=P（X≤x）。而分布函数与概率密度则是原函数与积分函数的关系，可表述为F'（x）=f（x）。分布律和概率密度之间又存在着积分关系，可表述为。上述三个等式成立的前提条件均为X是连续的随机变量，因为在离散型随机变量情况下，概率密度是不存在的。将随机变量函数应用到具体的数学分析积分问题中时，可以对复杂的积分问题进行简化。

　　2.4 其他方面的应用

　　概率论在数学分析中的应用范围是十分广泛的，除了上述提到的数学期望、中心极限定理以及随机变量函数以外，还有很多实际应用方面。例如，解决一些运用数学分析"积不出来"的问题，均可以使用概率密度函数进行转换，将原有的积分函数转化成密度函数，借助随机变量函数进行求解，打破了数学分析求解过程的局限性。总之，将概率论相关的定理、函数等应用到数学分析的解题过程中，可以解决一些确定的数学问题，再加上概率论自身就是用来解决随机的数学问题，使得概率论具备了同时解决确定问题和随机问题的特殊性质，成为了一门相对特殊的数学学科。

　　3 结论

　　数学分析与概率论存在着彼此渗透、互相转换的关系。数学分析是概率论研究与发展的基础保障，反之，概率论合理地应用到数学分析中也促进了数学分析的进一步发展，在很大程度上简化了部分数学分析问题的解题过程，提高了数学分析的解题效率。数学分析对概率论的影响主要体现在傅立叶变换、特征函数、公理化体系、中心极限定理和大数定律。而概率论对数学分析的影响则体现在数学期望、中心极限定理和随机变量函数的具体应用。两者的有机结合，在解决复杂数学问题上发挥着重要的作用。

　　参考文献

　　[1]彭劲。浅谈数学分析与概率论的相互关系[J].数学学习与研究，2019,（03）：33.

　　[2]邹涛。数学分析与概率论的相互关系研究[J].同行，2016,（07）：67-68.

　　[3]籍琳。论数学分析与概率论的相互关系[J].城市地理，2015,（04）：277-278.

　　[4] 田宁。浅谈概率方法在其他数学问题中的应用[J].中国化工贸易，2014,（10）：309-309.

　　[5]朱少平，王珍。概率论解题方法的一点思考[J].科技经济市场，2014,（06）：184-185.