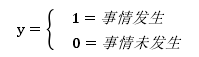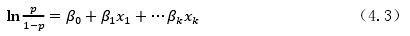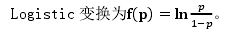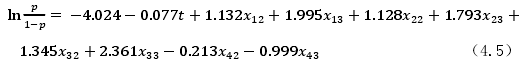本篇论文目录导航:
【题目】
中高端人才招聘网站中猎头行为探析
【第一章】
网络中猎头人群现状调查研究引言
【第二章】
Z招聘网站的成立与发展
【第三章】
网站猎头的行为分析
【第四章】招聘网站猎头活跃度
【结论/参考文献】
招聘网站注册猎头的特点研究结论与参考文献
4 猎头活跃度
网站的活跃用户,也称为网站的黏性用户,是网站用户的核心,对网站的发展起着关键作用。网站的活跃用户占比是衡量网站运营的重要指标。提高活跃用户的行为多样化,不断的吸收新的用户并增加活跃用户的数量和占比,才能实现网站的可持续发展。因此,衡量网站活跃用户的数量就显的尤为重要。
4.1方法介绍
本文使用 Logistic 回归展示不同的变量对活跃度的影响。
4.1.1 Logistic 回归理论
Logistic 回归模型是离散选择模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、市场营销、会计与财务等实证分析的常用方法。
Logistic 回归分析是对因变量为定性变量的回归分析。它是一种非线性模型。其基本特点是:因变量必须是二分类变量,若令因变量为 y,则常用 y=1 表示“yes”,y=0 表示“no”.自变量可以为虚拟变量也可以为连续变量。从模型的角度出发,不妨把事件发生的情况定义为 y=1,事件未发生的情况定义为 0,这样取值为 0、1 的因变量可以写作:
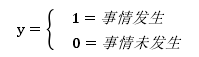
我们可以采用多种方法对取值为 0、1 的因变量进行分析。通常以 P 表示事件发生的概率(事件未发生的概率为 1-P),并把 P 看作自变量 x 的线性函数。由于 y 的取值在 0 与 1 之间,因此有如下分布:

所以 Logistic 变换能将接近 1 或 0 的这些 p 值分隔开。越是接近 1 或 0 的 p 值被Logistic 变换分隔的越开。
设相应变量 Y 仅取 0 和 1 两个值,p=P(Y=1)是我们的研究对象,设有 k 个因素x1,…,xk影响 Y 的取值,则称

为二值 Logistic 回归模型,简称 Logistic 回归模型。其中 k 个因素 x1,…,xk称为Logistic 回归模型的协变量。Logistic 线性回归模型是
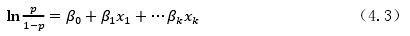

假设我们做了 n 次观察,其中对应于(x1,…,xk)的一个组合(xi1,…,xik)的观察值有 ni个,则 Logistic 回归模型的数据结构如小标所示:
根据这些数据,可以求得未知参数β0,β1,… βk 的极大似然估计值。
4.1.2 评价模型
需对建立的模型判断拟合的优劣。从系数检验、模型判别和模型校验以及模型的拟合优度等方面评价模型。
对于较大样本的系数检验,使用基于卡方分布的 Wald 统计量。当自由度为 1 时,Wald 值为变量系数与其标准误比值的平方。
模型校验,评估观测概率、预测概率与整个概率之间的关系,它对观测量概率与预测概率之间的差异进行解释。当协变量配对的数量巨大,且不能使用标准卡方拟合度卡方检验时,常用的检验方法 Hosmer 和 Lemeshow 卡方统计量检验。
模型的拟合度是用来判断模型与样本的拟合优劣。利用已有的参数,得出的观察结论的可能性称为“似然比”.似然比的值小于 1,习惯上用对数似然比值乘以-2 来度量模型对数的拟合度,记做-2ll.好的模型的似然比比值较高,其-2ll 值相对较小。似然比值的变化说明当变量进入与被剔除出模型时模型对数据拟合度方面的变化。
4.2数据的处理
用户拥有积分的数量可以衡量网站的活跃程度。积分是一个积累的过程,与猎头在网站注册时间有关。所以本文用“平均积分=总积分/注册月份”,得到平均每个月获得的积分数量,衡量猎头在网站的活跃度。平均积分高的用户在网站上更活跃。
网站运营数据显示,平均每个工作日大约有 4000 位猎头使用网站,由此,我们假定网站的活跃猎头用户大约占总数的 1/4.活跃用户指的是每天登录以及经常登录的用户。根据经验认为网站有大约 1/4 的活跃用户。根据数据的分布计算得到平均每个月获得不少于 100 个积分的用户被认为是网站的活跃用户。
因为其他获得积分的途径都是一次性的,只有发送推荐职位和回应求职者是可持续的途径。因此,模型忽略一次性影响因素,只考虑这两个行为对积分的正影响。推荐职位越多会获得越多的积分,同样的,回应次数越多也会获得越多的积分。
通过推荐职位等行为获得的积分可以用来下载简历,网站优秀的简历库为猎头搜寻人才提供了很多的便利。网站的作用在于给求职者和猎头提供一个桥梁解决存在的招聘信息不对称的问题,网站作为平台的作用是让猎头和求职者联系起来。而下载简历,只是猎头单方面的行为,会简化网站的用途,对网站的效用不大。所以,网站并不希望猎头单独下载过多的简历。更希望猎头和求职者之间互动从而达到互通信息的功效。因此,猎头下载简历会使积分减少。
网站为了降低发布虚假职位的风险,发布职位信息不会得到积分。但是,用户所有的行为均与职位有关,职位的发布是整个网站运营的基础,故将发布职位这个变量引进模型。
由于该数据属于时间序列的数据,随着时间的增加,变量的值会增长。为了剔除时间变量的影响,所有的变量都除以注册时间长度,得到平均每个月获得积分的数量,以此衡量网站猎头的活跃度。
工作经验对于猎头行业来讲是很重要的。通过上文的分析可以看出,经验丰富的猎头的主要工作是发布职位,比较年轻的猎头的工作是寻找人才。这样的结构,就会对猎头在网站的行为产生影响。不可否认的,工作经验,是影响猎头用户的一个指标。
我们将用户的活跃度作为因变量。取 y=1 是活跃用户,y=0 不是活跃用户。
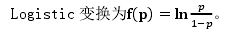
协变量为以下 5 个变量,t:工作经验、x1:发布职位数、x2:推荐职位次数、x3:回应次数、x4:下载简历次数共选取这四个代表猎头在网站行为的变量。因共有 11368条数据,协变量取值区间较大,需对变量进行分类。
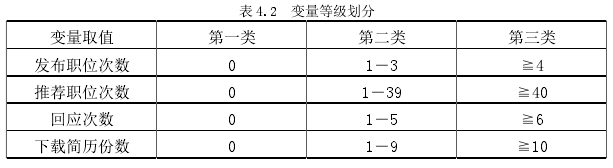
在上文中,主要是考虑指标的分布情况,以猎头的贡献率为依据来划分指标。将指标划分为三类,取值为 0 划为一类,贡献率较大的 5%的猎头为一类,其余的划分为一类。现在是要考虑猎头的活跃度 ,根据以上假定的约有 1/4 的用户属于网站的活跃用户的话,得到在变量排名高于 8526 的用户即被认为该变量的活跃用户。如此,将变量大致按以下类别划分。
4.3 Logistic回归拟合结果
4.3.1 Logistic 回归拟合结果
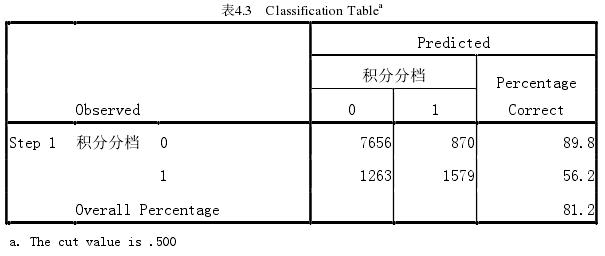
使用二元 logistic 回归方法,将协变量作为分类变量,使用 SPSS 软件对数据进行处理,可以得到以下结果,
模型总的正确判断率是81.2%,不活跃的猎头的正确判断率为89.8%,活跃猎头的正确判断率是56.2%.
在活跃的猎头判断中还存在缺陷。推测存在以下两个原因。第一,猎头获得积分的方式还有好多种,模型忽略了所有一次性获得积分的情况,查看数据确实存在猎头在网站的推荐职位、回应次数并不多,却通过其他方式得到很多的积分。第二,由于有一万多条的数据,存在很多的不确定性,导致了活跃用户分类的不可测度。
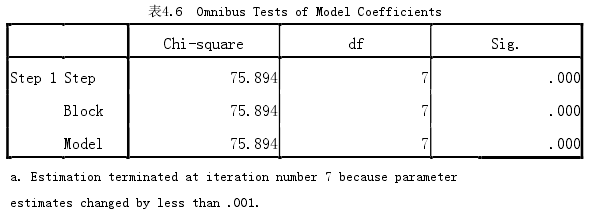
表4.6是3种常用的卡方统计量。判别模型与样本的拟合优劣。因为拟合方法选择的是默认的Enter,只有一步完成包含常数项与5个变量的模型的拟合,所以模型的Model、拟合过程块Block的和这一步的Step的卡方值完全相同。Sig值小于0.05,说明方程有意义。
表4.7是Hosmer-Lemeshow是拟合统计量,其原假设为方程对数据的拟合良好。该模型的sig>0.05,无法拒绝原假设。即该方程对数据的拟合良好。
因此,以上结果显示模型通过检验,得到回归方程为
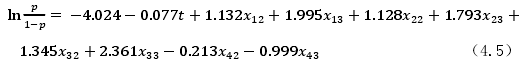
方程的变量为t=工作经验,x1=发布职位数、x2=推荐职位次数、x3=回应次数、x4=下载简历次数。其中,方程变量均已第一个类别作参考,其参数是指与第一个类别比较的变化。
4.3.2 结果分析
从方程可以看出,猎头的从业经验增加会导致积极性会下降,也就是新入职猎头行业中的人员会有较高的积极性。这与新进入该行业的猎头需要扩展人脉资源有关。而经验丰富的猎头一般都有了固定的企业客户,也已经建立自己的候选人简历库。新兴起的网络人才库的对其的吸引会降低。
发布职位行为不会奖励积分,但是,所有网站的行为包括推荐职位、回应候选人等都是以发布职位为前提,结果显示发布更多职位的猎头会活跃。
更多的推荐职位以及更多的回应次数都可以使猎头更活跃。可以看出来,下载简历的数量对猎头活跃度的影响最小。下载简历会降低猎头在网站的活跃度,因为下载简历行为从侧面说明了猎头可能没有发布职位和推荐职位的行为,而只是查找简历并且下载。不符合网站良性运转的目标。
该方程的建立删除了一次性获得积分的途径。因为网站的持续发展主要还是依靠可持续的行为来衡量运营效果。因此,该模型评价猎头活跃度的方式较积分更符合网站的实际需求。