利用RBF神经网络对白银现货价格进行预测

　　马克思说：“货币天然不是金银，金银天然是货币。”这句话揭示了白银在人类历史中不同寻常的作用和地位。

　　然而，在国际金本位制确立以后，白银逐渐淡出国际货币的舞台，其投资价值也慢慢被人忽视，白银沦为了黄金的附属品。

　　受金融危机的影响，2008年10月底白银从8.42美元/盎司开始逐渐上升，2010年加速上行，截至2011年4月25日，最高飙升至49.81美元/盎司，涨幅达到591%，而同期现货黄金价格从721美元/盎司涨到1920.78美元/盎司，涨幅仅为266%。

　　尤其是现货白银在2010年10月到2011年4月几乎直线式的飙升使人们意识到，白银也许比黄金更具有投资价值。

　　一、研究综述

　　20世纪80年代末，J.Moody和C.Darken提出一种具有单隐层的三层前馈网络，即RBF神经网络。RBF网络的特点是能够以任意精度逼近任意的非线性连续函数，可以模拟系统内复杂的函数关系，具有良好的泛化能力。

　　因此，RBF神经网络在时间序列分析、非线性价格预测等方面应用广泛。HamidKhaloozadeh利用前向神经网络的逼近性能对实际经济时间序列进行建模，通过对历史数据的训练学习，对经济数据进行预测，提出非线性RBF神经网络模型可以作为德黑兰价格指数（TEPIX）日常数据处理模型，并且这种非线性模型可以成功地用于长期预测TEPIX日常数据。吴薇、陈维强、刘波结合国内股票市场的特点,利用BP神经网络对沪市综合指数的走势进行了预测分析。

　　白雪冰分别使用BP和RBF神经网络对浙江经济增长进行预测，提出RBF神经网络拟合程度比BP神经网络好，但是预测能力不如BP神经网络的结论。

　　王旭东、邵惠鹤等人对RBF神经网络的原理、网络结构和算法进行了讨论，并且对RBF网络的应用情况作了介绍。

　　植俊文以车牌字符识别为例，构造了RBF神经网络，并与传统的BP神经网络进行对比，证明了RBF网络在车牌字符识别方面优于BP神经网络。

　　王京宝利用RBF神经网络对国内上市的股票价格进行预测,通过选取样本数据，对网络进行训练和仿真,建立起用于股票价格预测的RBF神经网络模型。

　　宋宜斌等人通过分析RBF神经网络原理，提出了一种用于对非线性对象模型进行拟合与辨识的RBF网络学习算法。

　　综合国内外学者的研究成果，BP神经网络能够很好地解决内部机制复杂的非线性问题，但是存在网络结构难以准确确定、网络训练失败的可能性较大、网络的逼近能力较差等问题，这些缺点限制了BP神经网络在经济预测方面的应用。

　　与之相比，RBF神经网络在预测方面的应用较为广泛，但是RBF神经网络主要应用于股市的预测，而将RBF网络应用于白银价格变动分析的研究比较少。

　　基于此，本文尝试建立RBF神经网络模型对国际白银现货价格变动进行分析。

　　二、RBF神经网络径向基函数

　　（RBF，Radical　Basis　Function）是多维空间插值的传统技术，由Powell于1985年提出。1988年，Broom-head和Lowe根据生物神经元具有局部响应的特点，将RBF引入神经网络设计中，产生了RBF神经网络。

　　（一）RBF神经网络结构

　　径向基函数神经网络(RBF网络)是一种前馈神经网络，一般为三层结构：输入层、隐含层、输出层，如图1所示。

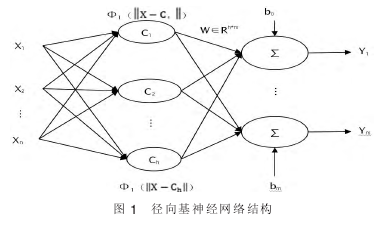
　　图1为n-h-m结构的RBF网，即网络具有n个输入，h个隐节点，m个输出。

　　其中X=（X1，X2，…Xn）T为网络输入矢量，W∈h*m为输出权矩阵，b0，…，bm为输出单元偏移，Y＝（Y1，…Ym）T为网络输出，Φ（*）为第h个隐节点的激活函数。

　　图中输出层节点中的Σ表示输出层神经元采用线性激活函数。

　　（二）RBF神经网络的学习算法

　　RBF网络有两个可调参数，即中心位置Cj和σj2方差（或称函数的宽度参数σ），此时整个网络的可调参数有3组，即各基函数的中心位置、方差和输出单元的权值。

　　一种较好地确定Cj和w的方法是用聚类方法实时调整中心，并同时调整中心和权值。

　　聚类方法就是把样本聚成几类，以类中心作为各RBF函数的中心，常用的方法有K均值法和自组织法。

　　下面介绍自组织法的学习步骤。

　　1.基于K-均值聚类方法求解基函数中心c第一步，网络初始化：随机选取h个训练样本作为聚类中心ci（i=1，2，…，h）第二步，将输入的训练样本集合按最近邻规则分组：按照xp与中心为ci之间的欧式距离将xp分配到输入样本的各个聚类集合谆p（p=1，2，…，p）中。

　　第三步，重新调整聚类中心：计算各个聚类集合谆p中训练样本的平均值，即新的聚类中心ci，如果新的聚类中心不再发生变化，则所得到的ci即RBF神经网络最终的基函数中心，否则返回第二步，进入下一轮的中心求解。

　　2.求解方差σi该RBF神经网络的基函数为高斯函数，因此方差可由下式求解，即

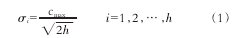
　　式中cmax表示所选取中心之间的最大距离。

　　3.计算隐含层和输出层之间的权值隐含层至输出层之间神经元的连接权值可以用最小二乘法直接计算得到，计算公式为

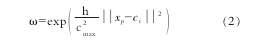
　　其中，p=1，2，…，P；i=1，2…，h。

　　（三）RBF神经网络的Matlab实现本文采用

　　Matlab7.0中RBF神经网络工具箱中newrbe函数，该函数用于设计一个严格径向基网络。

　　其调用格式为net=newrbe（P,T,spread）其中，P为Q组输入向量组成的R*Q维矩阵；T为Q组目标分类向量组成的S*Q维矩阵；spread为径向基函数的分布密度，spread越大，径向基神经元就能够对输入向量所覆盖的区间都产生响应，网络的预测性能越平滑。

　　但是并不是越大越好，过大的spread可能导致程序计算的时间过长。spread的取值对于newrbe函数十分重要，因此在下面的RBF网络设计的过程，将用不同的spread值进行尝试，以确定最优值。

　　三、实证分析

　　本文选取2008年10月24日至2013年8月2日共计205周的白银现货周收盘价（美元/盎司）进行实证研究，数据来源为易汇通交易软件。

　　在创建神经网络前，先对原始样本数据进行归一化处理，将数据归一化到之间。

　　处理的方法为Xi=（Yi-Ymin）/（Ymax-Ymin）（3）其中,Yi为原始数据样本；Ymin和Ymax分别为原始数据序列中的最小值和最大值。

　　为了分析白银现货价格的变动，以前k周的白银现货收盘价格为自变量，第n周的收盘价格为因变量，即Xn=f（Xn-k，Xn-k+1，…，Xn-1）（4）其中，k定义为时滞。

　　在下面的研究中，将时滞k设置为5周、10周和15周，对应的数据分为200、195和190组样本（数据划分方法如表1所示）。

　　在应用RBF神经网络进行预测时，径向基函数的分布密度spread的值将影响神经网络的预测能力。

　　为了对spread的值进行准确估计，将白银现货收盘价数据分为训练组，测试组和预测组：训练组在时滞为5、10、15时分别为前180、175、170组样本，主要的功能是对神经网络进行训练；测试组为训练组样本后10组样本，即第181~190组、176~185组、171~180组样本，主要功能是对spread的值进行估计；预测组为最后10组样本，主要功能是对白银现货价格进行预测。

　　下面在Matlab软件中建立RBF神经网络模型并对spread的值进行估计。

 

 

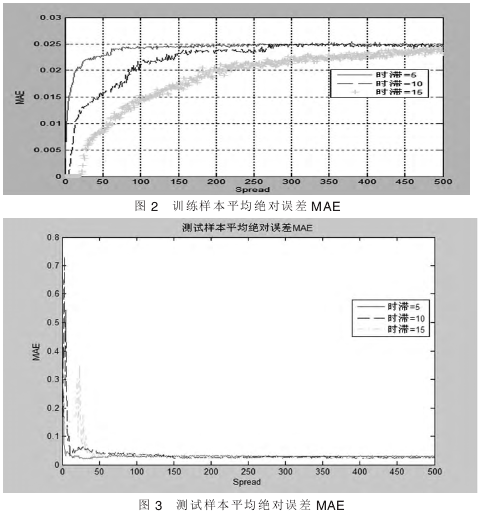
　　2为时滞分别取5、10、15，spread取值为1到500时训练样本的平均绝对误差（MAE），图3为时滞分别取5、10、15，spread取值为1到500时测试样本的平均绝对误差（MAE）。

　　从图2中可以看出，随着spread值的不断增大，训练样本的平均绝对误差不断增大，最后稳定于0.025，这表明神经网络模型的拟合精确度随着spread值的增大在不断下降，最后达到稳定。

　　当时滞为3周时，训练样本的平均绝对误差增大的速度最快，拟合精确度下降的最快；时滞为15周时，平均绝对误差增大的速度最慢，拟合精确度下降的最慢。

　　从图3可以看出，随着spread值的增大，测试样本的平均绝对误差先减小，然后增大，随后逐渐减小，最后稳定于0.022，这表明模型的预测精确度随着spread值的增大在不断提高，最后达到稳定。

　　当时滞为3周时，训练样本的平均绝对误差减小的速度最快，预测精确度提高的最快，在10~20之间预测精确度最高；时滞为15周时，平均绝对误差减小的速度最慢，预测精确度提高的最慢。

　　综合预测模型的拟合和预测精确度，当时滞分别为5、10、15时，spread的值分别取16、200、300。

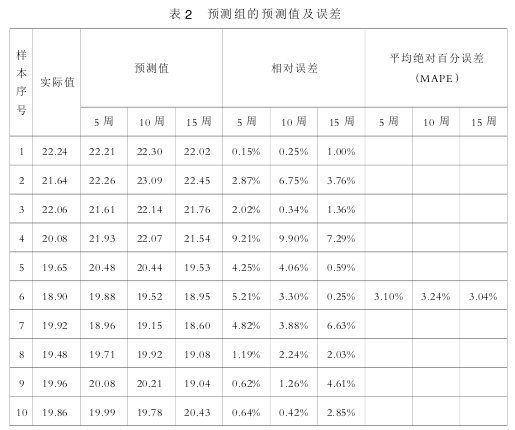
　　表2为spread取相应值时使用Matlab软件进行仿真输出的预测值和误差（数据经过反归一化处理）。

　　从表2中列出的预测值和相对误差来看，在三种时滞下，第4组样本的相对误差分别为9.21%、9.90%、7.29%，均明显大于其他样本的预测误差，原因是第4组样本的白银现货价格实际值较第3组样本的实际值发生的较大的变动，导致了模型未能很好地进行精确预测，这表明当白银现货的价格走势较为平稳时，RBF神经网络的预测效果较好，而当白银现货的价格剧烈波动时，RBF神经网络的预测误差较大。

　　当时滞为5周时，第4组样本价格的变动导致其后的3组样本的预测误差分别为4.25%、5.21%、4.82%，明显大于价格变动前的第1、2、3组样本误差值0.15%、2.87%、2.02%，表明第4组样本价格的变动对随后3组样本的预测精确度影响较大。

　　而当时滞为15周时，第4组样本价格的变动导致其后的3组样本的预0.022，这表明模型的预测精确度随着spread值的增大在不断提高，最后达到稳定。

　　当时滞为3周时，训练样本的平均绝对误差减小的速度最快，预测精确度提高的最快，在10~20之间预测精确度最高；时滞为15周时，平均绝对误差减小的速度最慢，预测精确度提高的最慢。

　　综合预测模型的拟合和预测精确度，当时滞分别为5、10、15时，spread的值分别取16、200、300。

　　表2为spread取相应值时使用Matlab软件进行仿真输出的预测值和误差（数据经过反归一化处理）。

　　从表2中列出的预测值和相对误差测误差分别为0.59%、0.25%、6.63%，第4组样本价格的变动对随后3组样本的预测精确度几乎无明显影响，这说明当时滞较长，相应的spread值较大时，模型对价格的突变不敏感。

　　从模型的平均绝对百分误差来看，当时滞分别为5、10、15周时，平均绝对百分误差很相近，为3%~3.3%，说明在三种时滞下，这10个预测样本的平均精确度为3%~3.3%，相差不大。

　　总体上，模型的预测效果较为理想。

　　如果考虑较大的spread值会会造成模型的拟合精确度降低，较小的spread值，即时滞为5周的模型是这3个模型中最合适的模型。

　　四、结语

　　从以上的研究分析结果上看，利用RBF神经网络对白银现货价格进行预测取得了较好的效果，对白银现货的投资具有很好的指导意义。

　　但是还有其他需要进一步研究的工作，如当白银现货的价格剧烈波动时，RBF神经网络的预测误差较大，并且会影响随后若干天的白银现货价格的预测精度。

　　对于这个问题，有三种解决方法可以供参考。

　　第一，对样本数据进行处理：以白银现货相邻两周的价格相除，再取对数，即白银现货的周收益率作为样本，这样可以减小数据的波动，或是利用小波理论等数据处理方法进行去噪处理，也可以考虑将波动剧烈的数据直接剔除。

　　第二，对RBF神经网络进行算法优化：使用混合粒子群算法、遗传算法或蚁群算法等方法确定RBF神经网络的隐节点个数和隐节点中心，对其中心向量及连接权值进行优化，以提高RBF神经网络的精度。

　　第三，建立其他更为合适的模型，比如支持向量机（SVM），RBF神经网络的优化目标是基于经验的风险最小化，这只能保证学习样本点的估计误差最小，而支持向量机对所有可能点的误差都达到最小，这使得支持向量机的预测能力强于RBF神经网络。

　　参考文献：
　　[1]飞思科技产品研发中心.神经网络理论与MATLAB7实现[M].北京：电子工业出版社,2005.
　　[2]宋宜斌,王培进.基于径向基函数神经网络的非线性模型辨识[J].计算机工程,2004(05).
　　[3]吴薇,陈维强,刘波.用BP神经网络预测股票市场涨跌[J].大连理工大学学报，2001(01).
　　[4]白雪冰.使用BP和RBF神经网络预测浙江的经济增长[J].企业研究,2010(16).
　　[5]王旭东,邵惠鹤.神经网络理论及其在控制中的应用[J].信息与控制,1997(04).
　　[6]植俊文,戴青云,黄雪贤.一种基于径向基神经网络的车牌字符识别方法[J].计算机应用,2005(12).
　　[7]王京宝.径向基函数网络（RBF）在股市预测中的应用[J].科技信息,2007(02).