CPI结构特征分解实证及短期预测

　　1 引 言
　　
　　2000 年至今， CPI 波动频繁、 幅度大， 一度高达8. 7% （ 2008 年 2 月） ,也有低至 - 1. 8% 的时期 （ 2009 年7 月） .按照国际惯例，CPI 在 2% ~ 3% 波动是属于可接受范围。CPI 过高会使得货币贬值，居民生活水平下降，同时使得市场价格失真，从而导致生产者盲目扩产； CPI持续大幅升高代表着恶性通货膨胀，造成严重的经济扭曲，引发社会动荡； 而 CPI 持续低迷会引发通货紧缩，致使失业率上升，甚至经济衰退。因此，如何科学探寻我国CPI 波动的结构特征、挖掘 CPI 的周期波动性和预测 CPI的趋势变化，对于旨在烫平经济波动的宏观经济政策具有重要的理论和现实意义。

　　目前已有不少文献对 CPI 的结构特征和预测进行了研究，这些文献运用的方法主要包括 ARIMA 类模型、协整理论、VAR 类方法、BP 网络神经模型等。例如王宏利（ 2005） 运用偏最小二乘法与 BP 网络神经模型对 2005 年CPI 进行模拟与预测，认为我国物价走势已经从货币政策为主转为宏观经济变量结构性控制为主。张成思 （ 2009）运用 grid - bootstrap 中值无偏估计和 VAR 模型分析 CPI 八大类子成分自身动态传导特征，发现其与总体 CPI 表现不同，货币政策本身的变化和不可预料的随机货币政策冲击对各分类 CPI 的影响存在差异。谭本艳和柳剑平 （ 2009）应用协整检验中的长期驱动和短期驱动的方法，从 CPI 分类指数的角度分析我国 CPI 波动的长期和短期决定因素。

　　王少平等 （ 2012） 建立 FVAR 模型，分析中国 CPI 的宏观成分和宏观冲击，研究结果证实 2010-2011 年这一轮的通胀是宏观因素驱动，并认为紧缩货币和需求能够有效抑制通胀。

　　尽管上述文献具备重要的参考价值，但仍存在一些值得商榷的地方。首先，已有文献多以纵向时间域的维度考察 CPI 波动率的时变特征 （ 如 ARIMA、GARCH 族簇、VAR 类模型） ,而忽略了在频率域维度上未显现的波动率时变特征，无法从时域和频域相结合的角度考察 CPI 的内在特征。其次，CPI 指数的变化受到政治、经济等多种因素的影响，变化规律复杂，各种影响因素间呈复杂的非线性关系，针对传统的预测方法不能很好反映这种非线性规律，导致对 CPI 指数预测精度不高。为了进一步剖析 CPI的波动特征与作用关系，同时提高 CPI 序列预测精度。本文运用国际上前沿的时频分析方法---EEMD 法，将分解之后得到的各 IMF 分量，针对其不同特征，分别建立相应的预测模型，这样更好地反映序列的随机性、周期性和趋势项特征，最后将各值叠加得到的组合预测值与采用单一模型预测值进行误差对比。

　　2 经验模态分解方法
　　
　　2. 1 经验模态分解 （ EMD） 理论与算法
　　经验模态分解 （ EMD） 是由 Huang et al. （ 1998） 提出的解决工程信号问题的方法，在自然科学等领域运用广泛。该法是基于时间序列内在的特征，自适应地通过筛选过程从序列中提取出不同频率的本征模态函数 （ IMF） ,它反映了序列内在的波动特性。EMD 可以解决时域和频域分析不能揭示各个频率分量在什么时刻出现的问题，是对以线性和平稳假设为基础的傅立叶分解和小波基等传统时频分析方法的重大突破 （ Huang et al. ,1998） .近年来，EMD 也开始应用于经济金融数据分析领域，如 Zhanget al. （ 2008） ,王晓芳和王瑞君 （ 2012） 等。

　　EMD 方法假设任何信号都是由一系列幅度和相位都随时间变化的 IMF 组成，这种 IMF 分量必须满足两个条件： 极值点个数和过零点数相同或最多相差一个以及其上下包络关于时间轴局部对称。从而把不同频率的波动和趋势从原序列一一剥离出来，具体步骤如下：第一，计算时间序列 s（ t） 的所有极大、极小值点；第二，由所有极大值和极小值根据三次样条插值来分别构造 s（ t） 的上下包络线；第三，根据求得的上下包络线，计算 s（ t） 的局部均值 m1（ t） 以及 s（ t） 与 m1（ t） 的差值 h1（ t） = s（ t） - m1（ t） ;第四，通常 h1（ t） 不是一个 IMF 分量，为此需要对它重复进行上述过程，直到 h1k（ t） = h1 （ k -1）（ t） - m1k（ t） 符合 IMF 的定义要求，即认为 h1k（ t） 是一个 IMF 分量，记c1（ t） = h1k（ t） ,r1（ t） = s（ t） - c1（ t） ,s（ t） = r1（ t） ;第五，重复以上步骤，直到 rn（ t） 小于已设定值或变为单调函数和 cn（ t） 满足给定终止条件，则序列 s（ t） 的EMD 筛选过程结束。

　　2. 2 集成经验模态分解 （ EEMD）
　　EMD 分解的一个重要缺陷是模态混叠---一个 IMF由多个频率不同的时间序列加总而成或者有相同频率的时间序列出现在不同的 IMF 中，使得 EMD 分解不彻底。为克服该缺陷，Wu & Huang （ 2009） 提出具有有效抗混叠分解能力的集成经验模态分解 （ EEMD） 方法，具体过程如下：

　　第一，s（ t） 加入白噪声 νi（ t） ,即 si（ t） = s（ t） +νi（ t） ;
　　第二，将新序列 si（ t） 进行 EMD 分解；
　　第三，重复上述步骤，每次加入不同的白噪声，把得到 IMF 的集成均值作为 EEMD 分解的结果。由白噪声的性质可知，随机白噪声可集成后相抵消，这样大大减小了模态混淆的机会。增加白噪声的效果可通过最终误差的标准差 εn来控制，即 εn= ε槡/ N ,其中 N 为加入白噪声的次数，ε 为白噪声的标准差。

　　3 CPI 结构特征分解实证
　　
　　本文选取 2000 年 1 月至 2013 年 6 月 CPI 同比数据进行研究，CPI 数据来源于中经网经济统计数据库。通过对CPI 序列描述统计可知， CPI 偏度为 0. 5356, 峰度为2. 7080,JB 检验为 8. 3216,在 5% 显着水平下拒绝服正态分布原假设，存在尖峰厚尾和序列自相关。

　　对 CPI 进行 ADF 检验和 GLS 检验的单位根检验可知，CPI 是一阶单整的时间序列。而 EEMD 方法是处理这类非平稳、非线性序列的有效工具，将其运用于 CPI 指数序列分析，可以从该序列自身出发揭示其内在特征。因此运用非线性非平稳的 EEMD 模型来分析 CPI 波动显得非常合适。

　　3. 1 EEMD 分解
　　通过 EEMD 方法，预先设定白噪声方差 ε = 0. 2 ,集成次数 N = 100 ,将 CPI 序列分解成 5 个周期不同的 IMF和 1 个余项。由图1 可知，被分解出来的 IMF 由高频向低频排列，振幅逐渐变大。而余项不存在周期性特征，是一个单调缓慢上升反应 CPI 长期趋势的时间序列。【图1】

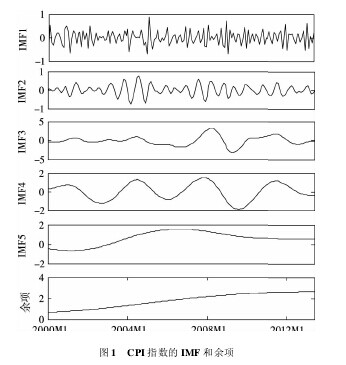
　　如表 1 所示，IMF1 和 IMF2 平均周期分别为 3 个和 7个月，其 Kendall 相关系数分别为0. 1037 和0. 1158.可认为 IMF1、IMF2 的波动属于不确定的随机因素成分，这些成分带有不确定性、周期短、发生频繁，导致与 CPI 序列相关系数小。IMF1、IMF2 方差占原序列方差总和均不超过 2%,表明 IMF1 和 IMF2 波动对 CPI 序列波动贡献率小。IMF3 到 IMF5 的平均周期均超过 1 年，反映 CPI 的中期和长期波动。这三个序列频率低，周期较长，波动缓慢但明显。且波动方向经常和原序列波动方向相同 （ 特别是 IMF3） ,导致其相关系数较高，这些低频 IMF 主导了CPI 序列走势，所以其对原始序列的方差贡献率很大。【表1】

　　余项的 Kendall 相关系数为 0. 3517,其序列变化平稳、缓慢、波动范围比 CPI 小。可将余项视为趋势项，体现 CPI 的长期走势。本文通过 EEMD 方法分解出的趋势项变化平稳、缓慢上升，且原始序列围绕其上下波动。所以用余项表示核心 CPI 序列比较理想，符合核心通货膨胀长期稳定性的要求。

　　3. 2 CPI 结构特征分析
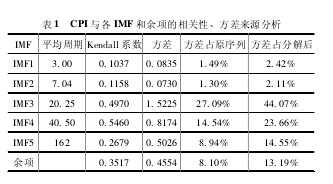
　　CPI 序列经 EEMD 分解成 5 个 IMF 和一个余项。IMF的频率各不相同，频率较高的 IMF 项表现出随机无序性，而频率较低的 IMF 项具有很强的周期性，余项则表现出一定的趋势性。从图 2 中可以看出，IMF1、IMF2 序列的均值近似等于零，从 IMF3 开始呈现出比较规则的周期性波动，且均值围绕零值上下分布。因此，将 IMF1、IMF2归为高频分量，而 IMF3 - IMF5 归为低频分量。【图2】

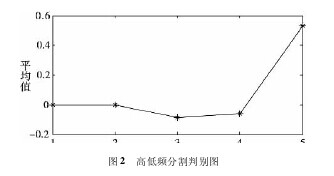
　　本文应用 EEMD 模态分解出不同频率的 IMF 和余项，这些频率不同的分量和余项分别隐含着很强的经济含义，可用来揭示蕴涵在 CPI 序列中的内在特征。高频分量振幅大小表示不均衡程度，可以用来揭示 CPI 短期的不均衡现象。但高频分量频率高振幅小，围绕零均值随机波动，对CPI 的影响有限； 低频分量的每次较大波动总是和一些大事件和外部冲击相对应，反映出一段时间内这些事件对CPI 序列的影响； 趋势项波动平缓，代表 CPI 内在运行轨迹。从低频分量来看，由表 2 可知，低频分量与原始序列的 Kendall 相关系数高达 0. 7695,其能解释 CPI 波动的75. 81% ,表明低频分量在 CPI 波动中占据的重要地位。

　　低频分量反映了我国 CPI 的中长期波动，重大事件对 CPI的影响主要体现在低频分量中，低频分量周期表示对 CPI产生影响的时间长短，振幅表示对 CPI 冲击的大小。从表1 可以看出， 最短低频 IMF 平均周期为 20 个月 （ 1. 7年） ,而且这些冲击对 CPI 波动影响非常大，表明短期内CPI 很难消除重大事件的冲击。如图 3 所示，2004 年粮食危机和投资热、2007-2008 年的国际大宗商品价格上涨冲击、2008 年国际金融危机、2012 年欧债危机。在以上这些时段内趋势项变化比较缓慢，而高频分量振幅又小，低频分量却与 CPI 同步大幅波动。所以低频分量是引起 CPI大幅波动最主要的原因，且短期内无法消除这些时间影响。

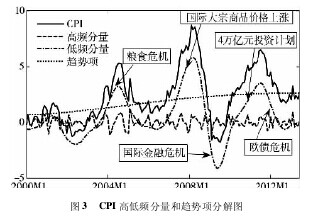
　　从趋势项来看，趋 势 项与原始序 列的 相 关 性 为0. 3517,方差贡献率 8. 10% .从图 4 可知，尽管 CPI 常受到一些外部的冲击大幅波动，但冲击影响结束后，指数仍返回到趋势项附近围绕其小幅波动，趋势项横穿整个 CPI序列，基本反映了 CPI 内在运行轨迹，可代表核心 CPI 的变动趋势。

　　4 CPI 短期预测
　　
　　CPI 是属于非平稳非线性的时间序列，传统的预测方法基本都是对整个时间序列进行预测，而没有充分考虑到时间序列的随机性、周期性和趋势性的特点，这样的方法会造成信息的损失，导致预测的精准度有限。因此，本文采用 EEMD 这种具有自适应的且适用于处理非线性非平稳序列的分解方法，把 CPI 序列分解成频率不同的分量，再根据各个分量不同的内在特征分别建立适当的 ARIMA模型，最后将各分量预测结果叠加作为 CPI 的预测值，即本文的 EEMD - ARIMA 组合叠加预测法。为检验预测效果，本文运用 ARIMA 模型对 CPI 原序列进行预测作为对比。

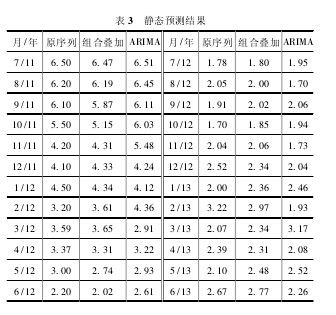
　　针对 EEMD - ARIMA 方法，对 IMF1 - IMF5 和余项分别建立 ARIMA 预测模型。表 3 列出了 24 期静态预测结果，即选取 2000 年 1 月至 2013 年 6 月 CPI 数据逐步预测2013 年 1 月至 2013 年 6 月 CPI 值。每预测完一期后，用实际值代替预测值对下一期进行预测，以此类推得出 24期预测值。从表 3 和图 4 可以看出，本文的 EEMD - ARIMA 预测方法与 ARIMA 预测方法相比，预测精度有明显提高。【表3.图4】

 

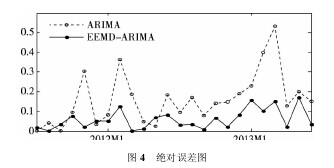
　　除个别月份外，EEMD - ARIMA 方法的绝对预测误差均小于 ARIMA 方法，说明 EEMD 分解可以分离出 CPI 中的随机性分量和周期性分量，从而可以更好地描述 CPI 波动的内在特征。总的来说，EEMD 分解对得到的各个IMF 和趋势项的特性，可以建立最合适的模型进行预测，同时充分考虑序列周期性、随机性和趋势性，从而提高预测精度。
　　
　　5 结 论
　　
　　本文基于 EEMD 方法，对我国 CPI 同比指数进行波动特征分析和短期预测。通过 EEMD 将 CPI 分解成频率 5 个不同本征模态函数和 1 个趋势项，进一步将其分为高频分量、低频分量和趋势项，这三个分量本质上代表着时间序列的随机因子、季节因子、循环因子和趋势因子。高频分量代表了 CPI 波动的随机性特征，反映了 CPI 的短期非均衡； 低频分量代表了 CPI 波动的周期性特征，反映了重大事件对 CPI 序列波动的影响，其平均周期较长，方差占序列波动的比重较大，说明 CPI 受重大事件的影响大； 趋势项主导 CPI 的长期走势，代表核心 CPI 的变动趋势。其次，利用经 EEMD 分解得到的不同特征分量，针对各分量不同的特征，建立相应的预测模型进行组合预测。组合预测结果与未分解直接用单一模型预测进行误差比较，研究发现分解后的预测效果更好。

　　参考文献：

　　[1] 王宏利 . 中国物件走势分析及其宏观调控 [J]. 世界经济，2005 （ 7） : 51 -59.
　　[2] 张成思 . 中国 CPI 通货膨胀率子成分动态传导机制研究[J]. 世界经济，2009 （ 9） : 3 -12.
　　[3] 谭本艳，柳剑平 . 我国 CPI 波动的长期驱动力与短期驱动力研究 [J]. 统计研究，2009 （ 1） : 50 -55.
　　[4] 王少平，朱满州，胡朔商 . 中国 CPI 的宏观成分与宏观冲击 [J]. 经济研究，2012 （ 12） : 29 -41.
　　[5] Huang N. E. ,Shen Z. ,Long S. R. The Empirical Mode De-composition and the Hilbert Spectrum for Nonlinear and Non - stationaryTime Series Analysis [J]. Proceedings of the Royal Society of Lon-don. 1998 （ 454） : 903 - 995.
　　[6] Zhang X. ,Lai K. K. ,Wang S. Y. A New Approach for CrudeOil Price Analysis Based on Empirical Mode Decomposition [J]. EnergyEconomics,2008 （ 30） : 905 - 918.
　　[7] 王晓芳，王瑞君 . 上证综指波动特征及收益率影响因素研究---基于 EEMD 和 VAR 模型分析 [J]. 南开经济研究，2012（ 6） : 82 -99.
　　[8] Wu,Z. H. and Huang,N. E. Ensemble Empirical Mode De-composition: a Noise - assisted Data Analysis Method [J]. Advances inAdaptive Data Analysis,2009,1 （ 3） :339 - 372.