对于定性指标,如方案灵活适应性、施工难度,很难直接给出隶属度。同时这些指标又是矿山建设必须考虑的因素,需要引入一种新的方法对其准确的计算。
这里采用二元对比排序法确定隶属度。具体方法如[12-13]:设U={u1,u2,…,un}为给定的论域,A为模糊概念,将ui与uj(i≠j)两元素进行比较,如果ui相对于uj具有A的程度值为cij,则uj具有A的程度值为cji.根据专家赋以模糊定量值,见表3.建立比较关系矩阵,由公式cji=fij/max(fij,fji)计算相对优先度函数cij,以cij为元素构造相对优先矩阵C,对矩阵C的每行取最小值,就可以得到各方案对该指标的隶属度。
2.4 综合评判由上述权重集W和隶属矩阵R,可以得到模糊综合评价集:

根据最大隶属原则,选择模糊综合评价集B=(b1,b2,…,bn)中最大的bj所对应的方案vj作为综合评判结果。
3实例应用
根据张家沟煤矿实际的地质条件和现具备的开采技术状况,将A1、A2、A3三个方案定为备选方案,各方面具体因素见表4.
3.1 计算各影响因素的权重
根据层次分析法的基本原理,结合专家打分,得到模糊判断矩阵A-B与层次权值单排序,见表5.
利用上文中公式和表5中各因素的权重值,经过计算得到λmax=1,CI=0,查表2可知对于3阶矩阵RI=0.58,计算得CR=0<0.1,可见判断矩阵B具有满意的一致性,因此求得的权重W=(0.286 0.250 0.571)可以在采矿方法优选时采用。类似的,可计算各个影响因素相对于评价准则的权重系数B1-U:B1=[1],CI1=0<0.1;B2-U:B2=[1],CI2=0<0.1;B3-U:B3=(0.310.193 0.04 0.04 0.31 0.067),CR3=0.083<0.1.
则可以得到层次总排序,见表6.
对总排序作一致性检验:CI=0.04,RI=0.753,CR=0.053<0.1,故符合一致性标准,因此层次总排序求得的权值向量W=(0.286 0.250 0.177 0.110 0.0230.023 0.023 0.177 0.038)可以在采矿方法选择中使用。
3.2 构建模糊综合评价矩阵
根据表4中所列采充总成本、最大暴露面积、采场生产能力、矿石损失率、矿石贫化率、采切比等影响采矿方法选择的6个定量指标,利用式(5)和式(6)计算得到隶属矩阵,正规化后为

对于表4中所列方案灵活适应性、通风条件、实施难度3个定性指标,利用上述二元对比排序法得到指标的优先度矩阵分别见表7、表8、表9. 可得3个定性指标的隶属度矩阵R7-9:
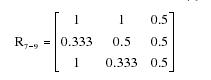
把定量隶属度矩阵R1-6与定性隶属度矩阵R7-9合并在一起,得到模糊综合评价矩阵R:

3.3 采矿方法模糊综合评判优选
利用以上所确定各因素的权向量W和模糊矩阵R,根据式(7)计算可得方案集A的模糊综合评判集为:
B=WR=(0.973 0.873 0.919)
由此可知方案A1的优先度大于方案A2和方案A3的优先度值,根据最大隶属原则,确定方案A1为该矿的最优采矿方法。
4结论
(1)张家沟煤矿采用利用层次分析法和模糊数学方法选择的方案A1,实践证明该采矿方法技术可靠、可操作性强、投产少、安全性好,达到了预期的优选目的。该矿从2007年到目前为止,每年的产煤量能确保在70万t以上,矿石损失率维持在15%以内,精矿品位达到55 %左右,取得了巨大的经济效益。可见,通过层次分析法和模糊数学法所选出的采矿方法更加科学、合理,具有非常好的实用性。
(2)在采矿方法选择中,大多数矿山通过历史经验和经济技术比较就能够选出比较满意的采矿方法,但对于一些开采技术条件相对复杂的矿山,在采矿方法传统决策的基础上,利用层次分析法确定各影响因素的权重,将多层次、复杂的目标分解为多个指标的若干层次,把具有模糊概念的定性指标的重要程度量化,减少了主观因素的影响,确保了评价结果的客观性。同时利用模糊数学理论对具有模糊性、不确定的信息进行全面和定量评价,减少了决策者的主观随意性,有效地提高了判断与决策的可靠性和准确性。
(3)目前利用层次分析法和模糊数学原理对备选方案进行优选在其他领域得到了广泛的应用,并且受到一致的好评,但是由于采矿工程本身的特殊性,在对各项权值分配及专家打分时,很容易受到对各项特征指标的限制;同时,当指标过多时,很难确定权重。如何克服还需要广大学者进一步研究。
参考文献:
[1] 肖福坤 , 张俊文 . 矿业系统工程 [M]. 江苏 : 中国矿业大学出版社 ,2010.96-97.
[2] 李俊芳。基于 AHP-FUZZY 多层次评判的城市轨道交通线网规划方案综合评价[J].武汉理工大学学报,2007,4(2):205-208.LI Junfang.Synthetic evaluation for urban rail transit line networkplanning scheme based on AHP-FUZZY method[J].Journal of WuhanEngineering University,2007,4(2):205-208.
[3] ALESIO Ishizaka,ASHRAF Labib.Review of the Main Developments inthe Analytic Hierarchy[J].Expert Systems with Application,2011,38(11):14 336-14 345.
[4] 王燕青,张秀艳。基于模糊层次分析法的民用机场安全风险管理[J].中国科学安全学报,2008,18(6)。WANG Yanqing,ZHANG Xiuyan.Risk management for civil airportssafety based on FAHP[J].Chinese Journal of Safety Science.2008,18(6):116-120.
[5] 邢剑,邢媛。基于 AHP 的 3G 无线宽带运营商选择方法[J].广西通信技术,2011(4):48-52.XING Jian,XING Yuan.3G wireless broadband operator selectionmethod based on APH[J].Guangxi Communications Technology,2011(4):48-52.
[6] 朱由创。基于层次分析和模糊数学的采矿方法选择[J].内蒙古煤炭经济,2014(12):131-133.ZHU Youchuang.Mining method choice based on AHP and fuzzymathematics [J].Inner Mongolia Coal Economy,2014(12):131-132.
[7] 刘玉龙,丁德馨,李广悦,等。层次分析法在铀矿山采矿方法选择中的应用[J].矿业研究与开发。2011,31(6):9-10.LIU Yulong,DING Dexin,LI Guangyue,Application of APH inoptimization of mining methods for uranium mine[J].Mining Researchand Development,2001,31(6):9-10.
[8] 孙小红 . 模糊数学与 Rough 集理论 [M]. 北京 : 清华大学出版社 ,2013,110-111.
[9] 董四辉,宿博。层次分析法的改进方法在煤矿安全评价中的应用[J].辽宁工程技术大学学报(自然科学版),2012,31(5):690-694.DONG Sihui,SU Bo.Improved analytic hierarchy process and itsapplication in coal mine safety assessment[J].Journal of LiaoningTechnical University(Natural Science),2012,31(5):690-694.
[10] 刘丹,王佳渊,彭关中。基于模糊层次分析法的导弹阵地防护效能评估[J].山西建筑。2007,33(1):72-73.LIU Dan,WANG Jiayuan,PENG Guanzhong.Missile position protectingefficiency assessment based on AHP and fuzzy mathematics[J].ShanxiArchitecture,2007,33(1):72-73.
[11] 叶海旺,常剑。基于模糊决策和层次分析法的采矿方法选择[J].武汉理工大学学报。2009,31(8):147-148.YE Haiwang,CHANG Jian.Choosing mining method based on fuzzydecision and analitic hierarchy process[J].Journal of wuhan universityof technology,2009,31(8):147-148.
[12] 谭玉叶,宋卫东,雷远坤,等。基于模糊聚类及层次分析法的采矿方法综合评判优选[J].北京科技大学学报,2012,34(5):493-494.TAN Yuye,SONG Weidong,LEI Yuankun,et al.Synthetic judgment formining method optimization based on fuzzy cluster analysis andanalytic hierarchy process[J].Journal of Beijing University of Scienceand technology,2012,34(5):493-494.
[13] 张小义,张红军。模糊数学在金川二矿区采矿方法优选中的应用[J].有色金属(矿山部分),2012,64(2):80-83.ZHANG Xiaoyi,ZHANG Hongjun.Application of fuzzy mathematicsin mining method optimization in Jinchuan N.2 minearea[J].Non-ferrousmetal(Mine Section),2012,64(2):80-83.



