落体法中摩擦力矩变化对转动惯量实验的影响

动力学论文第七篇：落体法中摩擦力矩变化对转动惯量实验的影响

 

　　摘要：为了分析刚体转动惯量实验测定中摩擦力矩变化对测量结果的影响, 本文对采用落体法测角加速度方法进行了实测检验。结果表明, 摩擦力矩随载物系统转速增大而显著增加, 系统空载测量时, 减速过程角加速度对应平均转速远大于加速过程平均转速, 如果不进行修正, 则导致计算结果偏低。而相同质量砝码拉动系统负载测量时, 加速过程和减速过程对应平均转速相对接近, 测量值主要受测量随机误差影响。上述结果有利于进一步开展转轴摩擦力矩随转速变化系统性的研究。

 

　　关键词：转动惯量; 摩擦力矩; 角加速度; 相对误差;

 

　　THE ERROR ANALYSIS IN MEASUREMENT OF RIGID BODY INERTIA BY THE FALLING BODY METHOD

 

　　GAO Feng GUO Changli BAI Bing

 

　　Department of Applied Physics , Xi'an University of Science and Technology

 

　　Abstract：In order to analyze the influence of the friction torque change on the measurement of rigid body inertia, the falling body method is used in the experimental analysis. It is indicated that the friction torque increases significantly with the increase of the system rotation speed, if the average rotation speed of the system in the deceleration process is much higher than that in the acceleration process, and if no correction is made, the calculation results are usually relatively small. At the same time, it is pointed out that the average rotation speed in the acceleration process and the deceleration process are relatively close to each other, the measuring value is mainly affected by the random error. The above results are helpful to further study the friction torque variations against the rotational speed.

 

　　测量刚体的转动惯量有着重要的意义, 其在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要的参量。对于形状规则的匀质刚体, 其转动惯量可直接用公式计算得到, 而对于不规则的刚体或非匀质刚体的转动惯量, 一般通过实验的方法进行测定。刚体的转动惯量实验测定的基本方法有扭摆法和落体法两种[1,2,3], 上述测定方法往往存在不同程度的缺陷影响测量结果精度。文献[4,5]提出了利用气垫的方法测转动惯量的思路, 不过测量过程容易使实验变的复杂。当前, 采用不同测量方法对比其测量精度及研究不同误差因素在转动惯量测量应用中具有重要的意义。本文通过详细的实验数据分析了落体法中摩擦力矩变化对实验结果的影响, 其结果有利于后期改进落体法中影响测量精度的误差因素。

 

　　1 落体法基本原理

 

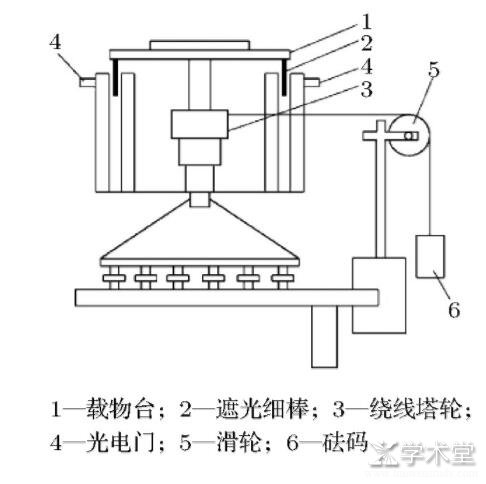
　　如图1所示, 在JM-3型智能转动惯量实验仪中, 载物台、塔轮构成一个可以绕中心轴转动的载物系统, 设它的转动惯量为J。半径为r的塔轮上绕一根细绳通过滑轮与质量为m的砝码相连, 当砝码由静止自由下落时, 拉动塔轮使载物系统转动, 滑轮及绳的质量忽略不计。

 

　

　　图1 转动惯量实验仪   

 

　　落体法可细分为测时间法、测角加速度法两种[6]。测时间法其测试量为不同质量m的砝码拉动塔轮转n圈的累计时间t, 拟合公式为m=k/t2+b, 采用作图法或最小二乘法拟合求得k和b, 由J=kgrt2/ (4nπ) 计算刚体转动惯量。测角加速度法的基本原理是在考虑转轴摩擦力矩的前提下, 通过测量仅在摩擦力矩作用下的减速情况的角加速度β1, 以及在砝码拉力力矩和摩擦力矩共同作用下的加速情况的角加速度β2, 由砝码下落的平动方程和载物系统转动方程联立求解得到载物系统的转动惯量

 

　　其中, β1为减速角加速度的绝对值。

 

　　文献[6]根据实测数据详述了测时间法和测角加速度法的优劣, 表明测角加速法可比测时间法的测量精度提高1?2个数量级, 具有明显优点。同时指出了采用角加速度法应注意:加速和减速对应的载物系统转速不能差别太大。这是因为, 转轴摩擦力矩与转速有关, 要保证摩擦力矩在加速或减速过程中基本一致, 需保证加减速过程的转速基本一致。采用一次过程测量β1和β2相比于分别测量法虽然提高了系统的稳定性 (详见文献[6]) , 但实际数据采集过程中, β1的对应的平均转速往往比β2对应的平均转速要高, 如果摩擦力矩增量明显, 会直接影响转动惯量测量精度。本文在下述内容中将针对摩擦力矩如何影响测量结果展开分析。

 

　　2 实验比较

 

　　JM-3智能转动惯量实验仪由MCS-51单片微型计算机等器件组成, 其电脑式毫秒计精度达到0.1 ms。根据光电门相邻脉冲计数时间间隔, 毫秒计可直接记录并存储运动过程中各角加速度值。同时, 为了保证记数正确, 加速过程变减速过程时毫秒计自动去掉5个相邻的角加速度值。本实验采用加速过程和减速过程同时测量的方法, 即砝码下落过程为加速过程, 砝码脱落以后为减速过程, 来获得原始测量角加速度各值。

 

　　考虑到启动时的摩擦力矩远大于正常转动时的摩擦力矩, 所以加速过程数据取样时舍去第一个值后依次取样相邻的6次β2, 减速过程取样为相邻的6次β1。具体操作为砝码质量m=50 g, 塔轮径r=2.0 cm时分别测量系统空载时的β1和β2及加待测圆环后系统负载时的β1和β2, 分别列于表1。控制载物系统其他变量, 仅改变砝码质量, 分别取100 g和150 g, 重复上述过程所测数据分别列于表2和表3。

 

　　表1 载物系统空/负载测得角加速度 (r=2.0 cm, m=50 g)     

 

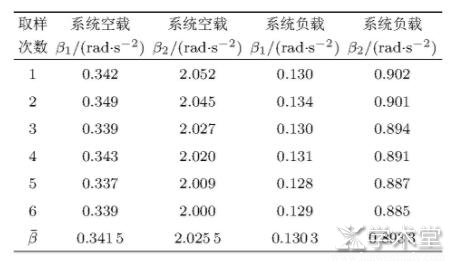
　　为减少因单次测量角加速度存在扰动引进新的统计误差, 各转动惯量的计算均取6次角加速度的平均值。表1?表3最后一行分别是各加减速过程6次取样值的平均值。令系统空载转动惯量为J1, 负载转动惯量为J2。将表1系统空载时的分别代入式 (1) 算得转动惯量J1=0.004 123 kg·m2。同理, 由表1数据计算得J2=0.009 556 kg·m2。改变砝码质量由表2和表3数据同理计算, 所测待测圆环的转动惯量及误差见表4第2?4行。

 

　　表2 载物系统空/负载测得角加速度 (r=2.0 cm, m=100 g)     

 

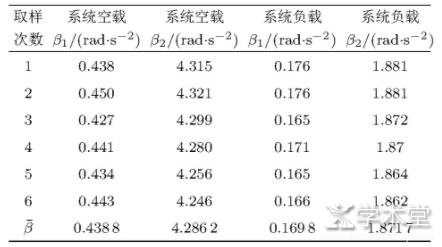
　　表3 载物系统空/负载测得角加速度 (r=2.0 cm, m=150 g)   

 

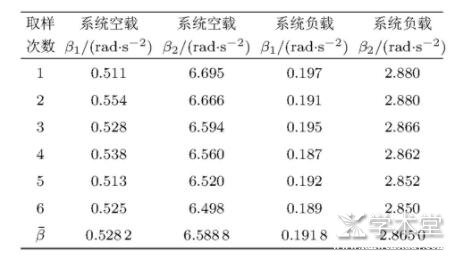
　　表4 测角加速度法测待测圆环转动惯量及误差 (待测圆环M=0.610 kg, D1=0.175 m, D2=0.200 m)     

 

　　

　　
        3 误差分析

 

　　测时间法由于摩擦力矩尤其是启动时的摩擦力矩无法估计会产生较大的误差。而测角加速度的方法中加速或减速过程都是正常转动以后的测量值, 与启动时的摩擦力矩无关, 因而误差较小, 表4中3种砝码质量下测角加速度方法相对误差都控制在近2%以内也说明这一点。但是, 摩擦力矩大小与载物系统转速有关, 由于加减速过程都是变速转动, 所以摩擦力矩在整个测量过程都是变量。例如, 表1?表3中系统空载减速过程的角加速度平均值分别为0.341 5 rad/s2, 0.438 85 rad/s2和0.528 2 rad/s2。其绝对值有很明显增加的趋势, 摩擦力矩对应不同转速并不是常数, 在常规测量中, 载物系统转速越高, 对应的摩擦力矩越大。所以摩擦力矩是否有效控制或抵消将直接影响测量结果精度, 接下来我们结合测量结果分别阐述摩擦力矩对测量精度的影响。

 

　　本文实验数据采用一次过程测量角加速量β1和β2, 即用砝码拉动, 先测外力矩和摩擦力矩共同作用下的加速情况的角加速度β2, 待砝码脱落后, 再测量减速过程的角加速度β1。这种方法首先消除了用手转动载物系统可能带来的系统不稳定性。但从表1?表3数据可以看出, β2值的大小相比β1高出约一个数量级, 而实际取样均为加速和减速情况的前段过程数据, 这表明, β1对应的平均转速要高于β2的平均转速。

 

　　式 (1) 计算中理论上要求加速和减速过程数据采集时转速基本一致, 由于减速过程转速较快摩擦力矩增加对应的β1要比理论值大, 因此式 (1) 需要修正为

 

　　其中, ?β1为修正量。β1对应的平均转速高于或低于β2的平均转速时, ?β1分别对应正值和负值。

 

　　一次过程测量角加速实验中β1对应的平均转速高于β2的平均转速时, ?β1分别对应正值。利用式 (1) 计算时β1未做修正, 则计算转动惯量较理论值偏小。另外, ?β1值的大小受下落砝码质量及载物系统转动惯量大小影响。系统转动惯量不变时, 砝码质量越大, 导致砝码脱落时刻系统获得的转速越大, ?β1修正量也应越大。表4第2?4行在砝码质量m分别为50 g, 100 g, 150 g时计算空载转动惯量J1分别为0.004 123 kg·m2, 0.004 112 kg·m2, 0.004 075 kg·m2, 随砝码质量的增加而减小。而当系统转动惯量较大时, 相同质量的砝码下落后不能达到较高的转速, 这种情况下是否修正的影响就会不太明显。表4第2?4行J2值的变化显示以随机误差为主。上述分析充分说明实验中摩擦力矩因系统转速变化, 即β1对应的平均转速高于β2的平均转速时对测量结果的影响。

 

　　表4第4列为不同砝码质量下J2-J1得到的待测圆环转动惯量实验测定值, 第5列为圆环理论计算值。比较第4, 5列可以发现, 第4列数值均大于第5列数值。因为J1受摩擦力矩变化影响严重, 所以计算值偏小;而J2的值变化以随机误差为主, 导致二者之差增大, 这和上面的分析是一致的。表4第6列分别给出了待测圆环实验测定值的相对误差, 整体误差可以控制在2%之内。但结果同样表明, 随砝码质量的增加, 误差程度出现增大的趋势。所以, 以减小摩擦力矩增量为目的的小质量砝码拉动测量操作能够有效提高实验测量精度。

 

　　4 结论

 

　　落体法测角加速度测量刚体的转动惯量在传统实验教学中往往忽略摩擦力矩随转速变化对实验结果的影响, 虽然测量结果能控制在较小的相对误差范围之内, 但不利于学生对实验中各种干扰因素的认知和了解。本文中通过改变砝码质量来改变系统转速, 可以清晰地给出, 当减速过程数据采集对应的平均转速远高于加速过程平均转速时, 由于摩擦力矩增大, 导致计算系统空载转动惯量的值相对理论值偏小, 这种偏差程度随下落砝码质量的增加而增大。其次, 载物系统负载较重时, 相同质量的砝码不能使减速及加速对应的平均转速差别过大时, 摩擦力矩变化对结果的影响就不是很明显。本文通过实测数据揭示了摩擦力矩变化对实验结果的影响, 进一步的分析将有利于开展转轴摩擦力矩随转速变化系统性的研究。

 

　　参考文献

 

　　[1]宋超, 潘钧俊, 叶郁文等.用三线摆方法测试物体转动惯量的误差问题.力学与实践, 2003, 25 (1) :59-61

　　[2]孟泉水, 班丽瑛, 朱金山.用复摆法测刚体转动惯量.西安科技大学学报, 2003, 23 (4) :478-480Meng Quanshui, Ban Liying, Zhu Jinshan.Measuring the rotational inertia of rigid body with the method of compound pendulum.Journal of Xi’an University of Science and Technology, 2003, 23 (4) :478-480 (in Chinese)

　　[3]王海林, 司嵘嵘, 李相银.落体法测量刚体转动惯量实验中引起测量值偏离的因素分析.物理实验, 2012, 32 (32) :25-30Wang Hailin, Si Rongrong, Li Xiangyin.Error analysis in measurement of rigid body rotational inertia by falling body method.Experiment in Physics, 2012, 32 (32) :25-30 (in Chinese)

　　[4]蔡静, 刘小廷, 李季平等.用气垫摆测物体的转动惯量.物理实验, 2000, 20 (6) :7-8

　　[5]陈淑清.用气垫转盘测转动惯量的数据处理及误差分析.物理实验, 2003, 22 (3) :13-15Chen Shuqing.Date processing and error analysis in measuring moment of inertia with air-cushion turntable.Experiment in Physics, 2003, 22 (3) :13-15 (in Chinese)

　　[6]郭长立, 李三庆.落体法测刚体转动惯量的测量方法比较.力学与实践, 2005, 27 (3) :69-72Guo Changli, Li Sanqing.Comparison of different methods of measuring rigid body inertia by the falling body law.Mechanics in Engineering, 2005, 27 (3) :69-72 (in Chinese)