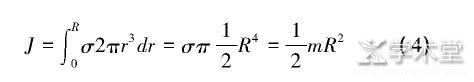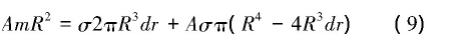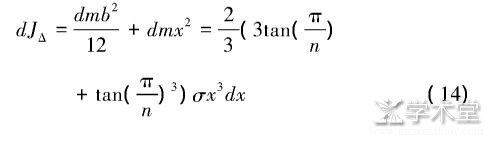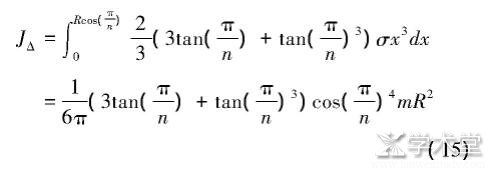三种计算圆盘类刚体转动惯量的方法探析

动力学论文第四篇：三种计算圆盘类刚体转动惯量的方法探析

 

　　摘要：刚体的转动惯量是大学物理刚体力学中的重点。研究采用了三种方法计算圆盘形状物体绕中心转动对称轴的转动惯量，即微元定义求解法、量纲分析法和等边n角形极限法。提出了后面两种巧妙的计算方法，引导学生在解决问题的时候开阔思维，激发其学习的积极性及对科研的探索精神。

 

　　关键词：圆盘; 转动惯量; 计算方法;

 

　　Three methods of calculating the moment of inertia of a disk

 

　　LAN Shan-quan

 

　　School of Physical Science and Technology,Lingnan Normal University

 

　　Abstract：The moment of inertia of rigid body is the focus of rigid body mechanics in university physics. In this paper,three methods are used to calculate the moment of inertia of a disk-shaped object about a central rotational axis of symmetry,namely,the method of solving the definition of micro element,the method of dimensional analysis and the method of limit of n-angle with equal sides. The last two ingenious calculation methods are put forward to guide students to broaden their thinking when solving problems,stimulate their enthusiasm for learning and explore the spirit of scientific research.

 

　　1 引言

 

　　转动惯量度量是刚体在力矩的作用下改变转动角速度的容易程度。它除了与刚体质量有关外，还与质量分布情况密切相关，也与转动轴的具体位置相关。转动惯量在刚体转动运动中的地位相当于质量在质点平动运动中的地位。而对于学生来说它又是一个新的物理量，所以转动惯量的引入、定义和计算都是教学的重点，求解常见刚体的转动惯量和相关讨论可见文献[1,2,3,4,5,6,7,8]。

 

　　本研究以圆盘为例，也适用于圆盘形状的其他物体(如圆柱)，计算了它们绕通过中心并且与盘面垂直的转轴转动的转动惯量[5,6,7,8]。具体介绍了三种计算方法，分别为:微元定义求解法、量纲分析法、等边n角形极限法。多种计算方法的讲解有助于加深学生的印象，提高其学习兴趣，更有助于开阔思维，激发其学习的积极性及对科研的探索精神。

 

　　2 圆盘转动惯量的计算

 

　　假设圆盘是匀质的，质量是m，半径是R，求它绕通过中心并且与盘面垂直的转轴转动的转动惯量。

 

　　2.1 微元定义求解法

 

　　解:第一步，求质量为dm，半径为r的细圆环绕转动对称轴的转动惯量dJ。

 

　　因为圆环上任何一点到转轴的距离都相等，所以等价。可以把它们集中于一点来考虑，从而变成了求质点的转动惯量。由定轴质点转动的转动惯量定义可以直接得到:

 

　　第二步，求圆盘转动惯量J。

 

　　把圆盘从中心点到最外围分为无数个细小圆环，计算各个圆环的转动惯量并求和。应用微积分的思想把求和变积分。

 

　　圆盘面密度为:

 

　　距离中心为r的圆环的质量为:

 

　　圆盘转动惯量为:

 

　　2.2 量纲分析法

 

　　解:圆盘绕其中心对称轴转动具有圆柱对称性，又由转动惯量的定义可知，它的量纲是质量和长度的平方，所以圆盘的转动惯量必定正比于它的总质量和半径的平方。把比例系数设为待定值A，从而可以写出圆盘的转动惯量为:

 

　　再在圆盘的最外围划出一个细小的圆环，圆环的宽度为dr，由此把圆盘分为两部分，即外围圆环和内侧半径为(R-dr)的圆盘。不难求出外圆环的质量为σ2π(R-dr)dr，而内圆盘的质量为σπ(R-dr)2。

 

　　从而可知外圆环的转动惯量为:

 

　　内圆盘的转动惯量为:

 

　　联立上面三式得:

 

　　令其中的dr为无穷小，并只保留一阶无穷小，上式简化为:

 

　　带入圆盘面密度可以算出:

 

　　最后得到圆盘的转动惯量为:

 

　　2.3 等边n角形极限法

 

　　解:把圆盘等分为n个扇形，连接每个扇形的底点，得到n个等腰三角形。当n趋于无穷大时，绕圆盘中心轴的转动惯量就等于n个等腰三角形绕圆盘中心轴的转动惯量。

 

　　第一步，计算顶角为2π/n的等腰三角形绕圆盘中心轴的转动惯量。

 

　　把等腰三角形平行于底边等间距分为无数个小长条，距离顶点为x，厚度为dx的小长条的长度为:

 

　　它的质量为:

 

　　由平行轴定理得该小长条绕圆盘中心轴的转动惯量为:

 

　　对上式从0到三角形底边高积分得等腰三角形绕圆盘中心轴的转动惯量为:

 

　　第二步，对n个等腰三角形的转动惯量求和，得到所求的圆盘转动惯量:

 

　　上式略去高阶项得:

 

　　上面三种方法所得结果一致。

 

　　3 结语

 

　　本研究采用三种计算方法得到了圆盘类刚体的转动惯量。三种方法中，第一种用到了微积分的思想，并且需要先求出圆环的转动惯量表达式;第二种用到了极限思维，量纲分析法很巧妙，也需要先知道圆环的转动惯量表达式。该方法在研究中很有用，就转动惯量的计算而言，还可以用在其他类型刚体上;第三种也用到了极限思维，虽然过程有些复杂，但是最是巧妙，其中的物理模型和思路都很清晰，并且求得了任意等腰三角形状刚体绕过等腰三角形顶点并与平面垂直的转轴转动的转动惯量。通过上面圆盘转动惯量的计算，展示了只要思维开阔、具有探究精神，就能够找到巧妙且有趣的方法解决所遇到的物理问题。

 

　　参考文献

 

　　[1]叶松.匀质三角薄板转动惯量的计算[J]．赤峰学院学报(自然科学版)，2018,34(07):9-10.

　　[2]李化南.刚体定轴转动讲授心得[J]．赤峰学院学报(自然科学版)，2008,24(04):33-34.

　　[3]赵强，韩春杰.刚体转动惯量的求解讨论[J]．物理通报，2014,(05):19-21.

　　[4]张金锋，刘建军，公丕锋，等.基于均质球对称刚体转动惯量的计算[J]．吉林师范大学学报(自然科学版)，2016,37(01):84-85,156.

　　[5]何艳，邓磊，谢艳丁，等.均质柱形刚体转动惯量的计算[J]．高师理科学刊，2016,36(10):46-48.

　　[6]杨小云.常见均匀刚体转动惯量的计算[J]．科技教育，2018,29(184):184-185.

　　[7]王建伟.刚体转动惯量的研究性学习[J]．喀什大学学报，2016,34(03):61-64.

　　[8]温亚芹.刚体转动惯量计算方法研究[J]．黑龙江科学，2019,10(06):40-42.