在高等数学教学中体现数学建模思想的方法

　　1 数学建模在煤矿安全生产中的意义
　　
　　在瓦斯系统的研究过程中，应用数学建模的手段为矿井瓦斯构建数学模型，可以为采煤方案的设计和通风系统的建设提供很大的帮助；尤其是对于我国众多的中小型煤矿而言，因为资金有限而导致安全设施不完善， 有的更是没有安全项目的投入，仅仅建设了极为少量的给风设备，通风系统并不完善。 这些煤矿试图依靠通风量来对瓦斯体积分数进行调控，这是十分困难的，对瓦斯体积分数进行预测更是不可能的。 很多小煤矿使用的仍旧是十分原始的采煤方法，没有相关的规划；当瓦斯等有害气体体积分数升高之后就停止挖掘，体积分数下降之后又继续进行开采。 这种开采方式的工作效率十分低下。

　　只要设计一个充分合理的通风系统的通风量，与采煤速度处于一个动态的平衡状态，就可以在不延误煤炭开采的同时将矿井内的瓦斯气体体积分数控制在一个安全的范围之内。 这样不仅可以保障工人的安全，还可以保证煤炭的开采效率，每个矿井都会存在着这样的一个平衡点，这就对矿井瓦斯涌出量判断的准确性提出更高的要求。

　　2 煤矿生产计划的优化方法
　　
　　生产计划是对生产全过程进行合理规划的有效手段，是一个十分繁复的过程，涉及到的约束因素很多，条理性很差。 为了成功解决这个复杂的问题，现将常用的生产计划分为两个大类。

　　2.1 基于数学模型的方法
　　（1）数学规划方法 这个规划方法设计了很多种各具特点的手段，根据生产计划做出一个虚拟的模型， 在这里主要讨论的是处于静止状态下所产生的问题。 从目前取得的效果来看，研究的方向正在逐渐从小系统向大系统推进，从过去的单个层次转换到多个层次。

　　（2）最优控制方法 这种方式应用理论上的控制方法对生产计划进行了研究， 而在这里主要是针对其在动态情况下的问题进行探讨。

　　2.2 基于人工智能方法
　　（1）专家系统方法 专家系统是一种将知识作为基础的为计算机编程的系统， 对于某个领域的繁复问题给出一个专家级别的解决方案。 而建立一个专家系统的关键之处在于， 要预先将相关专家的知识等组成一个资料库。 其由专家系统知识库、数据库和推理机制构成。

　　（2）专家系统与数学模型相结合的方法 常见的有以下几种类型： ①根据不同情况建立不同的数学模型，而后由专家系统来进行求解；②将复杂的问题拆分为多个简单的子问题， 而后针对建模的子问题进行建模， 对于难以进行建模的问题则使用专家系统来进行处理。 在整体系统中两者可以进行串行工作。

　　3 煤矿安全生产中数学模型的优化建立
　　
　　根据相关数据资料来进行模拟，而后再使用系统分析来得出适合建立哪种数学模型。 取几个具有明显特征的采矿点进行研究。 在煤矿挖掘的过程中瓦斯体积分数每时每刻都在变化，可以通过通风量以及煤炭采集速度来保证矿中瓦斯体积分数处在一个安全的范围之内。 假设矿井分为地面、地下一层与地下二层工作面，取地下一层两个矿井分别为矿井 A、矿井 B,地下二层分别为矿井 C、矿井 D. 然后对其进行分析。

　　3.1 建立简化模型
　　3.1.1模型构建表达工作面 A 瓦斯体积分数x·1=a1x1+b1u1-c1w1-d1w2（1）式中 x1---A 工作面瓦斯体积分数；u1---A 工作面采煤进度；w1---A 矿井所对应的空气流速；w2---相邻 B 工作面的空气流速；a1、b1、c1、d1---未知量系数。

　　很明显 A 工作面的通风量对自身瓦斯体积分数所产生的影响要显着大于 B 工作面的风量，从数学模型上反映出来就是要求 c1>d1.同样的 B 工作面（x·2）和工作面 A 所在的位置很相似，也就应该具有与之接近的数学关系式
　　
　　【2】

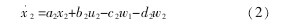
　　式中 x2---B 工作面瓦斯体积分数；
　　u2---B 工作面采煤进度；
　　w1---B 矿井所对应的空气流速；
　　w2---相邻 A 工作面的空气流速；
　　a2、b2、c2、d2---未知量系数。

　　CD 工作面（x·3、x·4）都位于 B2层的位置，其工作面瓦斯体积分数不只受到自身开采进度情况的影响，还受到上层 AB 通风口开阔度的影响。 在这里，C、D 工作面瓦斯体积分数就应该和各个通风口的通风量有着密不可分的联系； 于是 C、D 工作面瓦斯体积分数可以表示为【3】

　　
　　式中 x3、x4---C、D 工作面的瓦斯体积分数；
　　e1、e2---A、B 工作面的瓦斯体积分数；
　　a3、b3、c3、d3---未知量系数：
　　f1、 f2---A、B 工作面的瓦斯绝对涌出量。

　　3.1.2系统简化模型的辨识这个简化模型其实就是对于参数的最为初步的求解， 也就是在一段时间内的实际测量所得数据作为流通量，对上面方程组进行求解操作。而后得到数学模型，将实际数据和预测数据进行多次较量，再加入相关人员的长期经验（经验公式）。 修正之后的模型依旧使用上述的方法来进行求解，因为 A、B 工作面基本不会受 C、D 工作面的影响。

　　3.2 模型的转型及其离散化
　　因为这个项目是一个矿井安全模拟系统， 要对数学模型进行离散型研究， 这是使用随机数字进行试数求解的关键步骤。 离散化之后的模型为【1】

　　
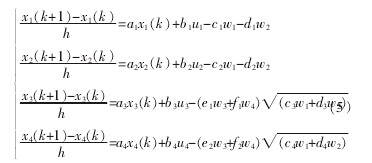
　　在使用原始数据来对数学模型进行辨识的过程中，ui表示开采进度，以 t/d 为单位，相关风速单位是 m/s,k 为工作面固定系数，h 为 4 个工作面平均深度。 为了便于将该系统转化为计算机语言，把开采进度 ui从初始的 0~1 000 t/d 范围，转变为 0 ~1, 那么在数字化采煤中进度单位 1 即表示 1 000 t/d, 如果 ui=0.5 就 表示每日产煤量500 t. 诸如此类，工作面空气流通速度 wi的原始取值范围是 0~4 m/s ,对其进行数字化，其新数值依旧是 0~1,也就表示这 wi取 1 时表示风速为 4 m/s,若 0.5 表示通风口的开通程度是 0.5,也就是通风口打开一半（2 m/s ），wi如果取 1 则表示通风口开到最大。

　　依照上述分析来进行数字化转换， 数据都会产生变化，经过计算之后可以得到新的参数数据，在计算的过程之中使用 0~1 的数据是为了方便和计算机语言的转换，在进行仿真录入时在 0~1 之间的一个有效数字就会方便很多。 开采进度 ui的取值范围0~1 表示的是每日产煤数量区间是 0~1 000 t ,而风速 wi取值 0~1 所表示的是风速取值在 0~4 m/s这个区间之内。

　　3.3 模型的应用效果及降低瓦斯体积分数的措施
　　以上对煤矿生产中的常见问题进行了相关分析，发现伴随着时间的不断增长瓦斯涌体积分数等都会逐渐衰减， 一段时间后就会变得微乎其微，这就表明这类资料存在着一个衰减周期，经过长期观测发现衰减周期 T≈18 h. 而后，又研究了会对瓦斯涌出量产生影响的其他因素，发现在使用炮采这种方式时瓦斯体积分数会以几何数字的速度衰减，使用割煤手段进行采矿时瓦斯会大量涌出，其余工艺在采煤时并不会导致瓦斯体积分数产生剧烈波动。 瓦斯的涌出量伴随着挖掘进度而提升，近乎于成正比，而又和通风量成反比关系。 因为新矿的瓦斯体积分数比较大，所以要及时将煤运出，尽量缩短在煤矿中滞留的时间，从而减小瓦斯涌出总量。

　　综上所述，降低工作面瓦斯体积分数常用手段有以下几种：①将采得的煤快速运出，使其在井中停留的时间最短；②增大工作面的通风量；③控制采煤进度，同时也可以控制瓦斯的涌出量。

　　4 结语
　　
　　应用数学建模的手段对矿井在采矿过程中涌出的瓦斯体积分数进行了模拟及预测，为精确预测矿井瓦斯体积分数提供了一个新的思路，对煤矿安全高效生产提供了帮助，有着重要的现实意义。

　　参考文献:

　　[1]陈 荣强 ,姚建辉 ,孟祥龙。 基于芯片控制的煤矿数控液压站的设计与仿真[J]. 科技通报，2012,28（8）：103-106.
　　[2]陈红，刘静，龙如银。 基于行为安全的煤矿安全管理制度有效性分析[J]. 辽宁工程技术大学学报：自然科学版，2009,28（5）：813-816.
　　[3]李莉娜 ,胡新颜 ,刘春峰。 煤矿电网谐波分析与治理研究 [J]. 煤矿机械，2011,32（6）：235-237.
　　[4]冯 伟东。 煤 炭采样设备研究及选型 [J]. 煤 炭技术 ,2013,32（9）：45-46.