原标题:生产管理中产品结构数据存贮模型研究

随着计算机技术的进步,计算机已越来越多的用于辅助生产管理。在企业的整个生产活动过程中,产品结构数据是一种重要的资源。产品结构是指产品的装配结构或产品的组成情况,具体地说就是组成产品所需的零部组件以及它们之间的关系。产品数据是指组成产品所需零部件的数据和描述这些零部组件之间的关系所需的数据的总和川。产品结构数据以什么样的形式存贮到计算机中去,主要取决于产品结构的特点。
研究工作是以某热工仪表厂生产调节阀系列产品的中型机械制造企业为试验基地进行的。
1、产品结构数据的分层存贮法
该厂生产的调节阀系列产品主要分五大系列44个品种,按不同的规格、型号共有近两万个不同的产品。其中相同系列产品通用件大量存在,数据存贮冗余度高,数据重复严重,因此合理地设计产品结构数据的存贮,建立优化的存贮模型十分重要。
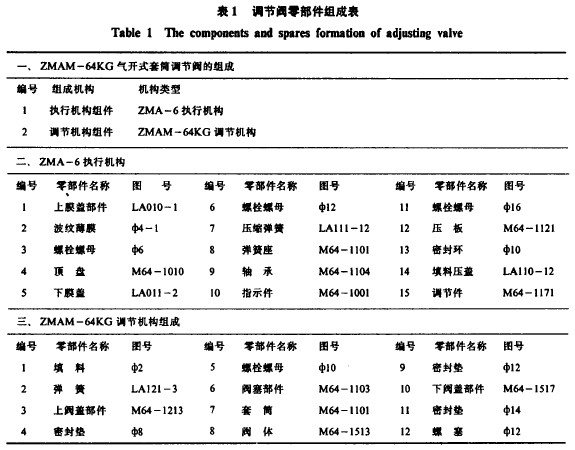
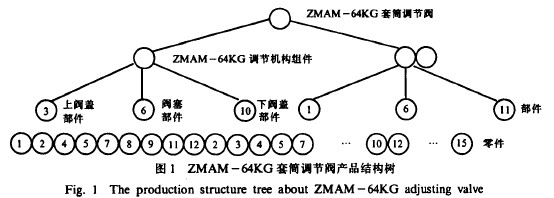
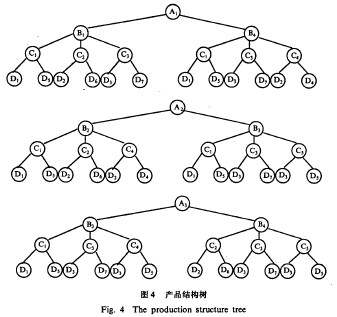
表1给出了该厂生产的气开式气动薄膜套筒调节阀(ZMAM一64KG)产品的零部件组成表。由表可知,产品结构数据之间一种复杂的多级层次关系,这种关系可以用图1所示的产品结构树形象地表示出来。
按照树的定义,图1所示产品结构树中的产品就是根结点,树中各子树的根结点组部件为树的分支结点,零件为树的叶结点。对于这样一种有层次关系的产品结构树,如果采用树结构的基本存贮方法存贮是不能令人示意的。因为只考虑单个产品本身的结构无法解决不同产品,组件中相同组件、部件的通用问题,使得数据冗余现象严重。浪费了存贮空间。
数据的冗余是由于数据间的相关性造成的,数据间的联系越紧密,数据的重复存贮越严重。为了消除数据间的相关性,实现存贮的共享,文中提出了产品结构数据的分层存贮法和层次矩阵存贮法。
在分层存贮法中,将产品结构树中的一株子树分离出来,作为一株独立的树,从而把一个多级层次的产品结构树分成多个两层的产品结构子树来存贮。分层存贮结构解决了通用件的重复存贮的问题。
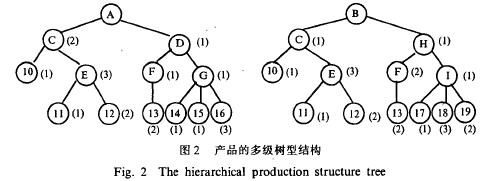
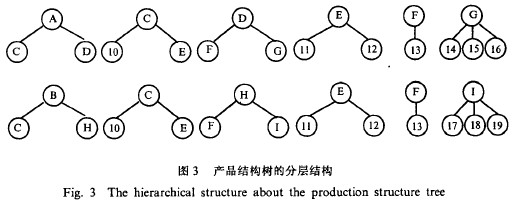
例如,图2给出了两棵产品结构树通用的抽象结构。它们可以被分解成图3所示一组子树。
这样,产品A和B就可以转化成分别存贮各自独立的子树。这些子树均是两层,可以用线性表来存贮。
从图3可以看出,产品A和B的结构中组件C、部件E和F三株子树相同,在分层存贮结构中,只需存贮一次,这就解决了数据的不必要的重复存贮。
在分层存贮结构中,结点数据项的个数与结点所包含下层子结构点个数有关,某一构件结点数据项个数Xi为该构件所包含下一级组成的个数Pi的两倍加1,即Xi=2Pi+1.各层结点之间通过链指针实现连结。
由于该企业的产品由组件,部伯,零件等组成,共四个层次,作如下假设:(l)该企业共有产品n种,组件n种,部件n2种,零件n3种;(2)每个产品由P1种组件组成,每个组件由P2种部件组成,每个部件由P3种零件组成每个零件包含P4属性。据此,我们可以计算出全。
部产品结构数据包含的信息数量为:产品结构信息:n,组件结构信息:n×Pi,部件结构信息:n×P1×P2,零件结构信息:n×P1×P2×P3.每个信息至少包含两个数据项内容,因此存贮全部产品结构数据共需存贮单元个数为:2n×(1+P1+P1×P2+P1×P2×P3)。
用分层存贮法存贮全部的产品结构数据,实际存贮的信息数量为:产品结构信息:n,组件结构信息:n1,部件结构信息:n2,零件结构信息:n3.共需存贮单元件数为:(2P1+1)×n+(2P2+l)×n1+(2P3+l)×n2+P4×n3.
即使在分层存贮结构中已经消除了通用的组部件的重复存贮,使由于通用件每出现在产品中都必须给以标识说明,所以实际上仍然有冗余存在。于是我们在本文中又提出了更佳的存贮方法一层次矩阵存贮法。
2、产品结构数据的层次矩阵存贮法
在产品结构数据的存贮中要存贮的不是某个单独的产品,而是企业所生产的全部产品。所有产品的结构树集合是一个丛,丛中不同树又有公用子树,矩阵元素恰好能表示这种关系。
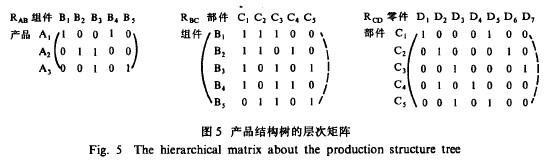
在多级树型结构产品的全体数据中,为每一层有直接从属关系(即层数之差为l)的数据建立一个相关矩阵,称为层次矩阵。以图4所示的产品A,,A2,A3的结构树为例,其层次矩阵可用图5形式表示。
这里,R(AB),R(AC),R(CD)分别表示产品一组件矩阵、组件一部件矩阵,部件一零件矩阵。
图中行代表某一级构件(产品或组件或部件),列代表其下一级构件(组件或部件或零件),元素R(ij)表示行i代表的构件Xi与列j代表的下一级构件Yj之间的关系。若Rij=0,则Xi不包含Yj,且数量为Rij.
如果产品品种很多,包含的零部组件的数量会相当大,因此层次矩阵是大型的矩阵。同时一种产品或组部件不能包含所有的下一级构件,而只能是其中的若干个,极小的一部分,所以层次差异阵又将是稀疏的矩阵。作为木型稀疏的产品结构层次矩阵若采用矩阵的一般存贮方法,将因存贮大量无意义的零元素而浪费空间。因此,进一步提出矩阵的压缩存贮技术。
(l)大型稀疏层次矩阵的压缩存贮。
压缩存贮技术就是把稀疏矩阵的非零元素的数值及相对应的行列索引同时存人[2].用三个长度为L的一维数组表示:YSSZ:存放非零元素的数值;YSHH二存放非零元素在原矩阵中的行号:YSLH:存放非零元素在原矩阵中的列号。其中L是稀疏矩阵中非零元素的个数。一般方法存贮一个m×m阶的稀疏矩阵,需存贮单元m×n个。而采用压缩存贮,而非零元素个数为L时,所需存贮单元数为3×L个。
(2)大型稀疏层次矩阵优化压缩存贮技术。
在优化压缩存贮结构中,仅存放稀疏矩阵非零元素的行号或列号,而行号或列号正负变换表示非零元素的存贮位置。这种结构只需两个一维数组来表示:SZ(K):逐行按列(或逐列按行)序存人非零元素的数值,长度为非零元素个数L;JS(K):非零元素位置检索数组,按SZ中顺序存人非零元素列序J(或行序I),当对应元素换行(列)时,加负号表示,长度与SZ相同。这样,存贮一个有L个非零元素的m×n阶稀疏矩阵需2×L个存贮单元。
3、产品结构数据存贮模型空间占用分析[3]
该厂可能生产的产品近20,000种,由于产品中通用件的大量存在,实际上组成产品组件的总数近5,000种,部件和零件的个数分别近2,000种和4,000种。又通过对产品结构的分析得知,每个产品包含2个组件:执行机构组件和调节机构组件;每个组件下面一般包含4个部件,每个部件包含5个零件;而每个零件用5个属性表示。这样,根据假设就有:
n=20,000,n1=5,000,n2=2,000,n3=4,000,P1=2,P2=4,p3=5,P4=5,于是,全厂产品结构数据存贮总信息量为:2x20,000(l+2+2×4+2×4×5)=2,040,000;采用分层存贮法存贮信息需存贮数量为:(2×2+l)×20,000+(2×4+l)×5,000+(2×5+l)×2,000+5×4,000=187,000:
采用矩阵的压缩存贮结构信息需存贮数量为:3×20,000×2+3×5,000×4+3×2,000×5=210,000,采用矩阵的优化压缩存贮结构存贮信息需存贮数量为:2×20,000×2+2×5,000×4+2×2,000×5=140,000.由此可见,分层存贮法将信息压缩了近11倍(2,040,000/187,000=11),矩阵压缩存贮的信息压缩程度为9~10倍(2,040,000/210=9.6),而矩阵的优化压缩存贮信息压缩的效果最突出,在15倍左右(2,040,000/140,000=15)。
4、小结
在大规模的数据存贮技术中,存贮空间和存取时间两个方面的优化是相互关联和相互制约的,分层存贮法和矩阵存贮法在降低数据存贮冗余度和提高存取速度和维护的可靠性方面取得了较好的统一,尤其适用于多品种小批量生产的企业解决品种多变、环境多变条件下的数据存贮问题。
【参考文献】
[1]Francis N D,Neelamkavil J.ComPuter Aided Production Planning in a Type Factory. Economics ComPutation and Economic Cybernetics Studies and Research,1980,3(14);
[2]杨绍棋,谈根林。稀硫矩阵一算法及其程序实现。高等教育出版杜,1986
[3]李莲治。姜文清,郭福顺。数据结构。大连理工大学出版社,1989