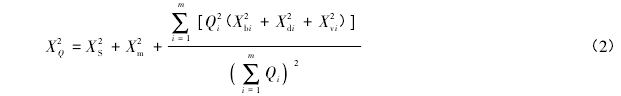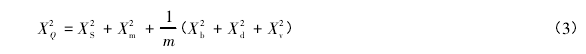摘要: 目前,测流不确定度通过误差试验或通过经验数值来确定,但这些方式存在着工作量大或不确定估计不足等局限性。为解决此问题,对基于实测数据和统计理论的插值方差估计法在不同测流条件下进行了验证,选取白河、襄阳和沙洋 3 个流量站进行了实测数据的不确定度分析,同时对白河站进行了 Monte Carlo 试验,比较插值方差估计法得到的不确定度与真实误差的差异。结果表明,插值方差估计法能较好地反映水位变化的影响,插值方差估计法所得到的不确定度与真实测流误差的相关系数达 0. 64,与断面水位变化的 Spearman 相关系数达 0. 79,高、中水位情况下插值方差估计法的不确定度估计结果较为合理,低水位情况下偏高。
关键词: 流量测量; 不确定度; 插值方差估计法; Monte Carlo 方法。
流量测量是水文测验中十分关键的部分。目前,大部分情况下,河流断面的流量数据是通过测量水位并根据水位-流量关系曲线换算而来。为了提高水位-流量关系曲线的准确性,国内外学者针对水位-流量关系研究方法进行了大量探讨。近年来,国内学者在水位-流量关系的确定方面,提出了单位线修正法[1]、综合单位线法、起涨水位法、落差指数法和下游水位参数法等多种计算方法[2].在水位-流量关系曲线拟合模型中,参数的推断则常有最大似然估计、最小二乘法[2]、贝叶斯方法[3-4]和水位流量双变量耦合演算模型[5]等方法,然而,这些方法无法规避单次流量测量不确定性带来的误差。文献[6]( ISO 748-2007) 提出了一系列基于实验和经验的测速、测深、测宽不确定度赋值表,由此可通过不确定度传递公式计算出单次流量测量的不确定度。在中国,评估不确定度的过程则相对复杂。最近修订的 《河流流量测验规范》( 简称“国标”)[7]要求,对于每个承担单次流量测量任务的水文站,均需进行误差试验,并通过误差试验来确定测速、测深、测宽的不确定度分量。然而,ISO 方法和国标方法都有其局限性: ISO 方法中,80%左右的不确定度来自于测量垂线数量不足[8]; 国内已有许多研究证实单次洪水即可使河道断面形状发生重大变化[9-11],国标所要求的误差试验将消耗大量的人力物力。在国标的指导下,国内相关研究往往限于误差试验的结果分析及测速垂线的布置手法。在国际上,文献[12]( ISO 25377-2007) 提供了测流不确定度的详细理论推导过程,将各种产生不确定度的因素纳入其中,但并不利于解决实际问题[12].文献[6]提供了适用于工程实际的不确定度计算方法及分量参考值,但参考值的代表性存疑,测线及测点数量引起的不确定度分量所占比例过大。针对文献[6]的缺陷,Le Coz 等[4]提出 Q+方法,后被 Despax 等[8]改进为 FLAURE 方法,这两种方法致力于提高 ISO 方法对测线和测点数量有限导致的不确定度分量的估计准确性。虽然上述两种方法的代表性及准确度相较 ISO 方法有所提高,但由于引入了通过经验确定的系数,使用门槛也相应提高。
Cohn 等[13]于 2012 年提出了用插值方差估计法( Interpolated Variance Estimator,文中用 IVE 方法表示) 来评估单次流量测量的不确定度,利用美国 Illinois 州 Fox 河的声学多普勒流速剖面仪( Acoustic Doppler CurrentProfilers,ADCP) 测流数据分析了 IVE 方法估计测流不确定度随垂线数目变化的情况。但在 Cohn 等[13]观测的时间段内,Fox 河平均流量仅 16. 4 m3/ s,缺乏代表性。本文着力于探索 IVE 方法用以估计不同条件下( 流量较大,高低水位时流量差距较大,断面形状较复杂) 测流不确定度时的性能,选取汉江白河站、襄阳站、沙洋站高、中、低水位的典型情况,对比分析国标和 IVE 方法计算的不确定度,并利用 Monte Carlo( MC) 试验对 IVE 方法进行检验,以判断 IVE 方法在分析形状复杂断面时的可靠性。
1 资料和方法。
1. 1 中国目前主要的测流及不确定度确定方法。
根据现行《河流流量测验规范》( GB 50179-2015) ,中国目前应用最广的测流方法即为流速-面积法[7],通过测速垂线对断面的流量进行分区计算并求和,其基本计算公式如下[6-7]:
式中: Q 为断面流量; m 为垂线数目; Ai、vi、bi、di分别为第 i 条垂线所代表的面积、平均流速、宽度以及平均水深; bi= ( xi+1-xi-1) /2,xi+1和 xi-1为第 i+1 和第 i-1 条垂线到岸边的距离。
由误差传递原理,文献[6]中将流量测量的不确定度计算公式表示如下:
式中: XQ为单次流量测验总不确定度; XS为校准测速、测宽和测深仪器之后残留的系统误差; Xm为测量垂线数量有限导致的误差; Xb i、Xd i、Xv i分别为第 i 条垂线测宽、测深及测速中的随机误差,%; Qi为第 i 条垂线所代表的流量[7].
在国标中,通过假设测流各部分的流量相等( 即等流量布线) ,并且各部分流量内各项源误差分别取等值[7]
,可将式( 2) 简化为:
根据流速的测定过程,第 i 条垂线流速的不确定度可以表示为[7]:
式中: Xci为仪器引起的不确定度; Xei为垂线水流脉动引起的不确定度; Xpi为计算规则及测点数不足引起的不确定度。