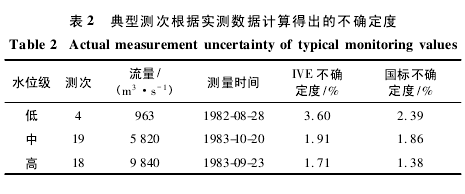
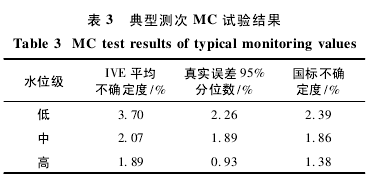
3. 2 MC 试验结果。
对白河站各测次利用 1. 4 节介绍的方法构造河流断面,并进行 MC 试验。在 MC 试验中,测宽不确定度Xb取为 2%[14],系统误差 XS取 1%.在分析真实误差时,取真实误差分布的 95%分位数进行分析,舍弃超过的 5%数据,使统计更具平均意义。在国标中,随机误差、未定系统误差以及允许误差均要求按照置信水平为 95%的不确定度来描述[7].IVE 方法在同一测次的 MC 试验中得出的不确定度有一定的随机性,波动幅度不大,取平均值进行分析。在已有研究中,IVE 方法的不确定度与真实误差的 95%置信水平相近[13].因此,选择真实误差的 95%置信度进行分析,有利于真实误差与国标不确定度、IVE 不确定度之间进行比较。
【图4】
图 4 中,y 轴为 IVE 确定的不确定度,x 轴为真实误差的 95%分位数。真实误差与 IVE 不确定度之间存在一定的线性回归关系,相关系数为 0. 36.同时存在着一个与回归线距离较远的点( 第25 测次的 MC 试验结果) .考虑到第 25 次属于枯水位级的特殊情况,将其去除后进行线性回归分析,相关系数提升至 0. 64.国标方法计算得到的不确定度与真实误差的 95%分位数相近。因缺少部分实验数据,本文采用了黄陵庙站的误差试验数据进行计算,因此,国标不确定度可能有一定的偏差。国标不确定度与真实误差 95%分位数的Spearman 相关系数为 0. 76,IVE 不确定度平均值与真实误差的 95%分位数的 Spearman 相关系数为 0. 79.
从白河站测次中选取第4、第19、第18 测次分别作为低、中、高水位的典型测次进行 MC 试验。表2 所示为典型测次根据实测数据计算得出的不确定度,表 3 所示为典型测次 MC 的实验结果。从 MC 试验结果来看,IVE 计算低水位级的不确定度偏高,中高水位则比较合理,同真实误差比较接近,而国标方法则相反。
4 结 论。
随着测流技术的发展和测流要求的提高,流速-面积法测流时测量的垂线数大大提高,IVE 方法得以应用。IVE 方法的统计分析特性使它更像一个黑盒方法,在分析的过程中得到测深不确定度和测速不确定度,而非测深和测流中的各误差分量。
IVE 方法在反映测流不确定度与水位之间的关系方面比国标方法好。国标方法分别考虑了高、中、低水位的情况,但并不能反映同一水位级中水位变化导致的不确定度变化。无论与国标相比还是与 ISO 方法相比,IVE 方法都存在不确定度偏大的情况。因此,IVE 方法可以认为是一种偏安全的不确定度分析方法。
从 MC 试验的分析结果来看,除第 25 测次之外,IVE 所计算的不确定度与真实误差存在明显的线性关系。
第 25 测次属于枯水位级,在枯水位情况下,IVE 方法的效果仍需进一步探讨。分析 MC 试验中高、中、低水位测次的典型情况结果表明,高、中、低水位时 IVE 估计不确定度均偏大,但低水位时偏大的程度较大。
由于 IVE 方法不需要进行误差试验,相比国标方法而言更加方便,可以作为河道剧变之后的临时方案对国标中的不确定度计算方法进行补充。IVE 方法也可以用在没有条件进行误差试验的情况,以便为后续工作提供不确定性分析的基础。
国标和 ISO 的不确定度估计方法都是基于误差试验或经验。本文通过对基于实测数据和统计原理的 IVE方法进行验证,证明了这类方法的应用价值。从 Monte Carlo 试验结果来看,IVE 方法仍有改进空间,尚需进一步研究。
参考文献:
[1] 包为民,司伟,沈国华,等。 基于单位线反演的产流误差修正[J]. 水科学进展,2012,23( 3) : 317-322. ( BAO W M,SI W,SHEN G H,et al. Runoff error updating based on unit hydrograph inversion[J]. Advances in Water Science,2012,23( 3) : 317-322. ( in Chinese) )。
[2] 万凤鸣,龙立华,张悦。 单值化处理长江中游主要断面水位流量关系研究[J]. 长江科学院院报,2012,29( 12) : 5-9. ( WANF M,LONG L H,ZHANG Y. Single valued processing of stage-discharge relation in the main cross section of Middle Reaches ofYangtze River[J]. Journal of Yangtze River Scientific Research Institute,2012,29( 12) : 5-9. ( in Chinese) )。
[3] 顾西辉,张强,陈晓宏,等。 基于贝叶斯方法的水位流量关系: 以东江干流为例[J]. 武汉大学学报( 理学版) ,2014( 4) :356-362. ( GU X H,ZHANG Q,CHEN X H,et al. Stage-discharge relationship based on Bayesian methods: a case study of EastRiver[J]. Journal of Wuhan University ( Natural Science Edition) ,2014( 4) : 356-362. ( in Chinese) )。
[4] LE COZ J,RENARD B,BONNIFAIT L,et al. Combining hydraulic knowledge and uncertain gaugings in the estimation of hydro-metric rating curves: a Bayesian approach[J]. Journal of Hydrology,2014,509: 573-587.
[5] 包为民,周俊伟,江鹏,等。 水位流速耦合演算模型研究[J]. 水科学进展,2015,26( 6) : 795-800. ( BAO W M,ZHOU J W,JIANG P,et al. Study of water-level and flow-velocity coupled routing model[J]. Advances in Water Science,2015,26( 6) : 795-800. ( in Chinese) )。
[6] International Standards Organization. Hydrometry-measurement of liquid flow in open channels using current-meters or floats: ISO748-2007[S]. Geneva: International Standards Organization,2007: 23-27.
[7] 水利部。 河流流量测验规范: GB 50179-2015[S]. 北京: 中国计划出版社,2015. ( The Ministry of Water Resources of thePeople's Repulic of China. Code for liquid flow measurement in open channels: GB 50179-2015[S]. Beijing: China PlanningPress,2015. ( in Chinese) )。
[8] DESPAX A,PERRET C,GARON R,et al. Considering sampling strategy and cross-section complexity for estimating the uncer-tainty of discharge measurements using the velocity-area method[J]. Journal of Hydrology,2016,533: 128-140.
[9] 孙东坡,刘明潇,张晓雷,等。 冲积性河流河床冲淤调整对洪水泥沙过程的响应: 以黄河游荡型河段为例[J]. 水科学进展,2014,25( 5) : 668-676. ( SUN D P,LIU M X,ZHANG X L,et al. Alluvial river adjusting response to the flood-sediment process:for the wandering reach of Yellow River as an example[J]. Advances in Water Science,2014,25( 5) : 668-676. ( in Chinese) )。
[10] 李洁,夏军强,邓珊珊,等。 近期黄河下游游荡段滩岸崩退过程及特点[J]. 水科学进展,2015,26( 4) : 517-525. ( LI J,XIA J Q,DENG S S,et al. Recent bank retreat and characteristics in the braided reach of the Lower Yellow River[J]. Advances inWater Science,2015,26( 4) : 517-525. ( in Chinese) )。
[11] 李志威,王兆印,李文哲,等。 卵石沙洲发育与冲刷试验[J]. 水科学进展,2014,25( 6) : 797-805. ( LI Z W,WANG Z Y,LI W Z,et al. Experimental study of development and erosion of gravel mid-channel bar[J]. Advances in Water Science,2014,25( 6) : 797-805. ( in Chinese) )。
[12] International Standards Organization. Hydrometry-hydrometric uncertainty guidance: ISO/TS 25377-2007 [S]. Geneva: Interna-tional Standards Organization,2007: 6-15.
[13] COHN T A,KIANG J E,MASON Jr R R. Estimating discharge measurement uncertainty using the interpolated variance estimator[J]. Journal of Hydraulic Engineering,2012,139( 5) : 502-510.
[14] 成金海,张年洲,黄化冰。 黄陵庙水文站流量误差试验研究[J]. 长江工程职业技术学院学报,2000( 1) : 10-14. ( CHENG JH,ZHANG N Z,HUANG H B. Study of flow test at Huanglingmiao Station[J]. Journal of Changjiang Vocational University,2000( 1) : 10-14. ( in Chinese) )。
[15] 刘伟林,郭爱军。《河流流量测验规范》有关水位级划分理论的商榷[J]. 长江工程职业技术学院学报,2011,28( 4) : 24-26. ( LIU W L,GUO A J. Discussion about the theory of water level partition in river discharge measurement criterion[J]. Journalof Changjiang Vocational University,2011,28( 4) : 24-26. ( in Chinese) )