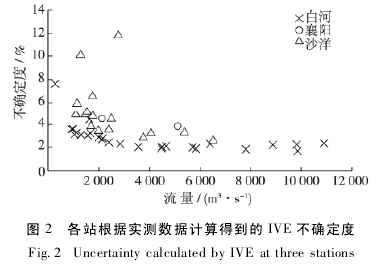
根据白河、襄阳、沙洋 3 站的实测流量数据计算得到的 IVE 不确定度如图 2 所示。从测次较多的白河及沙洋两站来看,IVE 计算不确定度体现出了中、高水位不确定度较为稳定,低水位不确定度偏大的情况。这种情况可能有两个原因,一是低水位情况下一般会减少测流垂线数量,二是测速及测深的系统绝对误差并不会随着水位降低而减小。3 个水文站 IVE 计算不确定度存在着一定出入。在流量相近的情况下,沙洋站不确定度高于白河站。襄阳站两个测次均属于高水位情况,不确定度也相近,但高于沙洋站及白河站高水位情况下的不确定度。3 个水文站的计算结果说明除水位及垂线数外,其他因素诸如地形、流速分布等也会影响计算的结果。因篇幅所限,选取测次数较多并覆盖高、中、低水位级的白河站进行详细分析,并对比 IVE 方法与国标方法的计算结果。
国标计算测流不确定度计算公式参考式( 5) .由于无法进行流量测验误差实验,式( 5) 中各不确定度分量的取值参考黄陵庙水文站在 1997 年开展的流量Ⅰ、Ⅱ、Ⅲ型误差试验及当时长江大站各水文站仪器、测深和测宽误差试验的最大值[14].黄陵庙水文站隶属于水利部长江水利委员会水文局,坐落于湖北省宜昌市夷陵区。黄陵庙水文站位于长江葛洲坝与三峡大坝之间,白河水文站位于长江支流汉江上,两站的断面类型和测量条件类似,因此,选取黄陵庙作为参考。文中除了国标计算不确定度的分量取值参考黄陵庙水文站之外,MC 试验的单次测深、测速误差也是根据黄陵庙水文站的误差试验确定。采用黄陵庙水文站的流量Ⅰ、Ⅱ、Ⅲ型误差试验进行计算,势必与实际情况有所出入,但由于黄陵庙水文站与白河水文站存在诸多相似性,在本文中,对比较的结果影响不大。
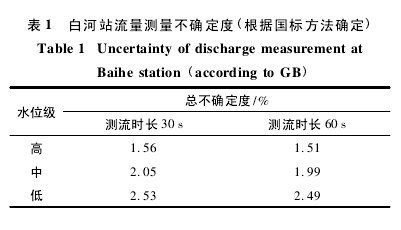
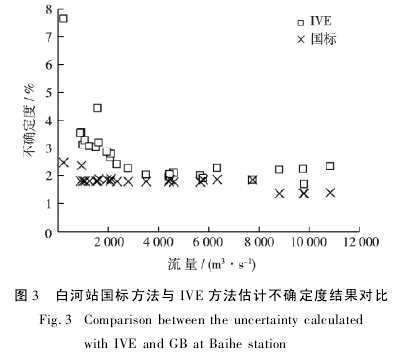
由于黄陵庙水文站在Ⅲ型误差试验中,最多只进行了 20 线的试验,而白河站所用的实测数据测线数在38 线至 64 线之间。在下述分析中,选择将 20 线的Ⅲ型不确定度代入计算总不确定度。因国标方法计算不确定度的过程中,同水位级下计算结果仅受垂线数影响,同时因数据中垂线数都较大,计算结果变化幅度小,因此,表 1 中仅展示各水位级下的总不确定度最大值。白河站的高、中、低水位级根据国标法取181. 00 m、173. 00 m、172. 00 m[15].水位级确定时考虑了白河站来水时间较短,采用值根据国标法计算值进行了调整,因此,最终确定的水位级中,低水位级可能出现流量大于多年平均流量的情况。IVE 方法参考式( 12) ,为与国标结果进行合理比较,Xd和 Xv使用 IVE 方法计算,XS和 Xb则根据国标中使用的值代入。图 3为国标方法与 IVE 方法的不确定度计算结果对比。
IVE 方法的计算结果与流量的 Spearman 相关系数为 - 0. 84,国标方法与流量的 Spearman 相关系数为-0. 58,二者都表现出负相关性,即不确定度随流量 / 水位降低而升高的特性。当 Q = 253 m3/ s 时,IVE 计算得出的不确定度达到 7. 67%.