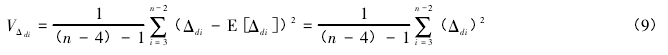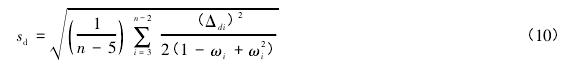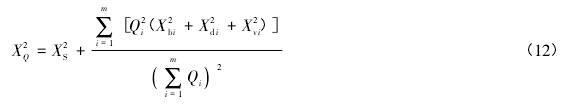同时,Δdi的方差也等于样本的方差,则:
通过对比式( 8) 和式( 9) ,可以得到 sd的计算公式如下:
根据式( 10) ,IVE 方法确定的第 i 条垂线测深的随机不确定度可以表示如下:
测速的随机不确定度计算方法与测深类似。由于 IVE 方法将 Xm合并进 Xdi和 Xvi的确定过程中,式( 2) 中的 Xm可以省略,IVE 方法的不确定度计算公式如下:
IVE 方法是一种基于统计理论的测流不确定度评估方法,适用条件为测量断面的测线与测点数量足够多,能够满足统计理论的基本要求。测流技术的发展,如 ADCP 等新型技术的应用,使得 IVE 方法能够普及。
1. 3 Monte Carlo( MC) 试验。
利用水文站实测数据,对每个测次进行 1 000 次 MC 试验,并从中选出高、中、低水位的典型测次进行分析。根据实测数据构造河流断面的思路如下:
( 1) 利用已知实测水深,对垂线中的空隙进行插值。每两个垂线间可以取 50 个构造垂线;( 2) 对每个插值垂线的深度乘上一个随机系数,以模拟自然情况下的不规则河床。对实测垂线则不进行调整;( 3) 构造垂线的平均流速取相邻两个实测垂线平均流速的线性插值;( 4) 根据以上测深及平均流速,将其作为实际情况,求出“真实流量”;( 5) 对原测线及测点进行 MC 试验。因测量水深及流速一定为正数,因此,测量随机误差系数选择为服从期望为 1 的 Gamma 分布随机数。
1. 4 Spearman 相关系数。
Spearman 相关系数,又称秩相关系数,用来评估单调函数描述两个变量之间关系的效果。在没有重复数据的情况下,如果一个变量是另外一个变量的严格单调函数,则二者的 Spearman 相关系数即为 1 或-1.Spearman 相关系数适用于以下情况: ① 数据的测量值未知,只有数据的排序信息已知; ② 数据之间为非线性相关。因此,Spearman 相关系数度量两变量之间联系强弱的效果更为准确。
本文研究的问题中,流量的实际值未知,同时估计的不确定度与实际测量之间的关系未知,因此,在分析真实误差与国标和 IVE 方法计算所得不确定度的相关性时,采用 Spearman 相关系数对 MC 试验结果进行分析。
2 实际案例。
本文运用 IVE 方法计算了汉江上白河站、襄阳站、沙洋站多次测流的不确定度。在对 3 个水文站进行简单分析的基础上,取实测数据较多,同时涵盖高、中、低水位的白河站数据进行深入分析并进行了 MC试验。
白河水文站是汉江上的重要水文测站,建于 1936 年,位于陕西省白河县。白河站上游流域面积为59 115 km2,白河站多年平均流量为747 m3/ s.本文使用白河站 1982-2006 年以来部分流量测量数据,共 26测次,测流方法为流速仪法,大部分测次选取的垂线数目为 46 线至 64 线之间。襄阳水文站建于 1929 年,位于湖北省襄阳市。在丹江口水库蓄水运用以后,由于主要来水来沙条件的改变,襄阳水文站水文特性逐步发生了变化,涨冲落淤幅度减小。沙洋水文站建于 1929 年,位于湖北省沙洋县。沙洋附近河道冲刷剧烈,上、下游两岸崩塌严重,沙滩、沙洲常年游荡冲淤不定。白河站、襄阳站、沙洋站虽同属汉江流域,但其断面形状、冲刷情况、水文特性各有不同,具有一定代表性。
3 结果及分析。
3. 1 国标和 IVE 方法计算结果。