计量经济学论文

您当前的位置：学术堂 > 经济学论文 > 计量经济学论文 >

计量经济学课程论文（教授热荐10篇）

来源：学术堂 作者：万老师
发布于：2019-11-25 共6900字

　　计量经济学是一门分析研究具有随机性特性的经济变量关系的学科，以济理论和统计资料为基础，运用数学、统计学方法与电脑技术，以建立经济计量模型，本篇文章主要给大家介绍几篇计量经济学课程论文，供给大家作为一个参考。

计量经济学课程论文教授热荐10篇之第一篇：计量经济学课程教学中的"四步法"

　　摘要："四步法"可以将计量经济学的原理和方法的核心呈现出来， 让晦涩难懂的厚厚的一本计量经济学教科书变得"越来越薄", 从而收获良好的理论教学效果。本文主要对"四步法"在模型和参数的显著性检验以及计量经济学检验中的具体应用进行了探讨， 旨在为学生学习和掌握其他所有的假设检验方法提供思路。

　　关键词：四步法； 课程教学； 计量经济学；

计量经济学

　　一、引言

　　《计量经济学》是一门面向经济学类各专业开设的专业必修课，1998年教育部高等学校经济学学科教学指导委员会确定计量经济学为经济学门类各专业的八门核心课之一。著名计量经济学家、诺贝尔经济奖获得者克莱因教授指出："在大多数大学和学院中，计量经济学的讲授已经成为经济学课程中最权威的一部分",对其他专业课的学习起到非常重要的作用。

　　但从教学实践上来看，各普通高校普遍存在着"学生难学"和"教师难教"的双重困境，因而引发了教师们的广泛关注和讨论，学者们从计量经济学的教学理念、教学模式、教学方法等各方面进行了大量的研究。比如，王乃静和李国锋（2001）、黄雪燕 （2006） 、李锐（2009）在教学过程中结合Eviews、R软件等应用软件探究了计量经济学教学的难点问题；胡新艳和陈文艺（2006）提出了"探究（Exploration）-讨论（Discussion）-实践（Practice）"教学模式；万冰魂等（2018）将成果导向教育（Outcome-based Education）理念引入计量经济学课程教学，从培养目标、教学内容、教学方法和考核方式4个方面设计了OBE改革的具体内容；叶霖莉（2017）和王文静（2017）则提出了问题导向式教学（Problem-based Learning）与案例教学（Case-based Learning）双轨教学模式以及刘冬萍（2018）基于任务驱动式教学（Task-driving Teaching）及问题导向式教学（Problem-based Learning）的"三线一体"教学模式试图改进传统计量经济学讲授式教学的弊端。

　　这些研究对提升计量经济学教学效果具有很好的参考价值。但是，计量经济学毕竟是一门理论性和实践性都很强的课程，学生只有牢牢掌握了计量分析的原理和方法，才能灵活地运用其解决实际的经济学问题。在有限的课时内，用计量经济学软件来教授计量经济学，可能产生这样一种误导：学习计量经济学就是学会软件的操作，既不知道输出结果是如何形成的，也不知道如何解释输出结果，更不知道基于输出结果提出相应的更有意思的问题（王少平等，2011）。我们也不应该在各种教学模式下迷失了正确的方向，因为计量经济学教学的核心是引导和启发学生掌握好计量分析的基本原理和基本方法。鉴于此，笔者在对大学本科生计量经济学教学内容进行系统分析和探究的基础上，运用"四步法"将计量经济学的基本原理和方法的核心内容呈现在学生面前，让晦涩难懂的厚厚的一本计量经济学教科书变得"越来越薄",收获了良好的理论教学效果。

　　二、"四步法"在计量经济学教学中的实施

　　计量经济学教学的主要内容包括：线性与非线性回归分析、多重共线性、异方差性和自相关性等内容，其中线性回归分析是各种计量分析的基础。一个完整的线性回归分析包括建立模型、估计参数和检验模型。因为教学大纲只要求学生能依据经济理论建立相应的计量经济学模型，参数的估计方法相对来说也比较简单，所以这部分内容对学生来说并不难掌握。但是，包括模型的显著性检验、参数的显著性检验以及多重共线性、异方差性和自相关性的各种检验，内容繁多且容易混淆，学生在学习过程中总觉得很困难，不容易掌握。因此，笔者对显著性检验和包含多重共线性、异方差性和自相关性检验的计量经济学检验进行了系统的分析和探究，提出了行之有效的"四步骤"法。

　　1. 显著性检验的"四步法"

　　在具体教学中，我们首先引入假设检验的基本思想，即假设检验本质上是一个带概率性质的反证法，并且将假设检验归纳为"四步骤"或戏谑地称之为"假设检验四步走":

　　（1）提出原假设H0,备择假设H1;

　　（2）构造检验统计量并计算统计量的值；

　　（3）给定显著性水平α，查出临界值；

　　（4）判定：依据小概率事件发生拒绝原假设进行判断。

　　传统回归分析中的假设检验主要包括模型的显著性检验F检验和参数的显著性检验t检验，两者在定义上是完全不同的两种检验，但是我们可以把这两种检验都用上述"四步骤"表示出来。假设总体线性回归模型的形式为：Yi=β0+β1X1i+…+βkXki+ui （i=1, 2,…，N），其中Y是被解释变量，Xj=（j=1, 2,…，k）是解释变量，ui为随机误差项，βj （j=0, 1, 2,…，k）为回归参数。根据定义，模型的显著性检验F检验的待检验假设为H0β1=β2=…=βk=0,而参数βj的显著性检验t检验的待检验假设为H0:βj=0.

　　因此，基于以上的假设，模型的显著性检验---F检验可以写为：

　　（1）提出原假设H0:β1=β2=…βk=0,备择假设H1:β1, β2, …βk中至少有一个不为零；

　　（2）构造并计算统计量的值，其中ESS为回归平方和，RSS为残差平方和；

　　（3）给定显著性水平a,查出临界值Fa;

　　（4）判定：如果F>Fa则拒绝原假设，如果F≤Fa则不能拒绝原假设（依据小概率事件发生拒绝原假设归纳）。

　　类似地，参数的显著性检验---t检验也可以表示为以下四个步骤：

　　（1）提出原假设H0:βj=0,备择假设H1:βj≠0;

　　（3）给定显著性水平a,查出临界值tα/2;

　　（4）判定：如果则拒绝原假设，如果则不能拒绝原假设（依据小概率事件发生拒绝原假设归纳）。

　　很容易可以看出，模型的显著性检验和参数的显著性均可以从本质上统一为"假设检验四步走".所不同的是两种检验的待检验假设不同，F检验和t检验分别形成了不同的原假设和备择假设，并且运用服从不同分布的统计量（分别是F统计量和t统计量）对其进行检验。而一旦检验统计量的分布确定了，则后面两步均是给定一个显著性水平，依据小概率事件发生拒绝原假设进行判定。

　　2. 计量经济学检验的"四步法"

　　我们在包含异方差检验、自相关检验和多重共线性检验在内的三大计量经济学检验的教学过程中，将每一种看似不相同的检验归纳为一个本质上完全相同的模块（或步骤）。由于篇幅限制，本文仅以异方差性的White检验和自相关性的BG检验为例，说明"四步法"在计量经济学检验教学中的应用。

　　假设线性回归模型Yi=β0+β1Xi+ui （i=1, 2, …， N）中，误差项的方差不再是一个常数或者说会随着观测值Xi的变化而变化，即ui的方差满足：var （ui）=σi2=h （Xi），说明存在异方差性。异方差性的White检验的原假设为Ho:满足同方差性，备择假设为H1:存在异方差。毋庸置疑，异方差的检验必然要通过一个"假设检验四步走"进行推断。但是White检验的检验统计量是一个服从卡方分布的LM统计量，该统计量的计算需要构造一个辅助回顾模型：σi2=α0+α1Xi+α2Xi2+εi,然后通过该辅助回归模型的判定系数R2来计算LM统计量的值，并且要能够估计该助回归模型得到R2的值，需要先估计出原模型的残差值u赞i,以u赞i2代替σi2才能进行估计。这就意味着，异方差性的White检验最终是进行一个"假设检验四步走",但在此之前要首先估计原模型和一个辅助回归模型，具体步骤如下：

　　估计原模型，得出原模型的残差平方u赞i2.

　　估计辅助回归模型u赞i2=α0+α1Xi+α2Xi2+vi,得出辅助回归模型的R2.

　　（1）提出原假设Ho:满足同方差性，备择假设H1:存在异方差；

　　（2）计算拉格朗日乘子统计量LM=n×R2, n为辅助回归模型的样本容量；

　　（3）给定显著性水平α，查出临界值Xa2;

　　（4）判定：如果LM>Xa2则拒绝原假设，如果LM≤Xa2则不能拒绝原假设（依据小概率事件发生拒绝原假设归纳）。

　　假设线性回归模型Yi=β0+β1Xi+ui （i=1, 2, …， N）中，误差项ui存在q阶自相关性即满足ui=ρ1ui-1+ρ2ui-2+…+ρqui-q+εi,则自相关性的BG检验的待检验假设为H0:无q阶自相关性，BG检验也可以表示为类似White检验的步骤：

　　估计原模型，得出原模型的残差平方u赞i.

　　估计辅助回归模型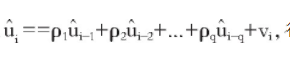得出辅助回归模型的R2.

　　（1）提出原假设H0:无q阶自相关性，备择假设H1:存在q阶自相关性；

　　（2）计算拉格朗日乘子统计量LM=n×R2, n为辅助回归模型的样本容量；

　　（3）给定显著性水平α，查出临界值Xa2;

　　（4）判定：如果LM>Xa2则拒绝原假设，如果LM≤Xa2则不能拒绝原假设（依据小概率事件发生拒绝原假设归纳）。

　　与显著性检验相比，这两个不同的计量经济学检验方法在估计了原模型和相应辅助回归模型之后，最终的判定均是依据"假设检验四步走",除了待检验假设不同以外，假设检验的思想和步骤完全相同。显而易见，计量经济学教学的"四步法"就是要体现"假设检验四步走"在各种检验方法中的核心地位。这种教学方式可以引导和启发学生将基本原理和方法的核心呈现出来，让厚厚的一本计量经济学教科书变得"越来越薄",从而获得良好的教学效果。

　　三、结语

　　计量经济学教学的"四步法"是以"假设检验四步走"为核心的教学方法，目的是引导和启发学生掌握好计量分析的基本原理和基本方法，激发学生学习枯燥的计量理论的兴趣，同时有效地提高计量经济学理论教学的效果。由于篇幅原因，本文没有详细罗列出所有检验方法的"四步骤"法，但是所有的假设检验方法都是可以通过"假设检验四步走"实施，只是不同检验的待检验假设不相同，当我们选定了检验统计量以后，均只需要依据小概率事件发生拒绝原假设就可获得最终的结论。

　　参考文献
　　[1]万冰魂， 周恩德， 李雪涛。基于OBE理念的计量经济学教学改革研究[J].决策与信息， 2018 （12） :26-31.
　　[2]胡新艳， 陈文艺。EDP教学模式在计量经济学教学中的应用[J].高等农业教育， 2006 （4） :58-60.
　　[3]叶霖莉。PBL+LBL双轨教学模式在计量经济学教学中的应用探讨[J].湖北经济学院学报 （人文社会科学版） , 2017 （3） :135-137.
　　[4]王文静。 PBL&CBL教学法在计量经济学教学实践中的应用[J].统计与管理， 2017 （9） :48-51.

计量经济学课程论文教授热荐10篇之第二篇：计量经济学课程理论与实践研究

　　摘要："学而时习之， 不亦说乎？", 学得道理并适时的加以实践练习， 是一件令人心生喜悦的事。这种强调知行合一、学以致用的观点， 自古以来就是正确的。然而， 现阶段学习计量经济学的现状却仍停留在理论层面， 缺乏解决实际问题的能力， 计量经济学的理论知识教授了很多数据分析方法， 显然将其与现实生活的实际相结合是必要的， 加强实验教学、案例教学、重视实际问题建模、重视计量经济学软件应用， 对实现计量经济学的理论与实践的结合具有重要意义。

　　关键词：计量经济学理论； 实践应用；

　　一、计量经济学理论与实践中存在的问题

　　计量经济学是经济理论、统计学、数学、计算机的结合， 因为其强大的功能和众多实用的方法已经成为经管类专业基础课程之一， 正是因为这个特点， 计量经济学的学习会使部分同学望而生畏， 因为在这几门学科结合之下产生的计量经济学理论难度不容小觑， 而在这几门学科都有较好的学习基础的同学也为数不多， 这就造成了在计量经济学实际学习过程中会遇到很多问题。

计量经济

　　大多数老师比较重视理论知识的传授， 在实际生活中计量经济学的实践应用也有很多障碍， 其原因有三， 一是课时的限制， 因为计量经济学理论具有一定难度， 讲解需要花费很多时间， 在这样的情况下很难再展开诸如问题建模等实践教学， 二是在大多数计量经济学教材中都不重视数据来源和建模的方法介绍， 而将重点放在如何检验模型中了， 这对于在实际生活中应用计量经济学解决问题形成了知识障碍， 三是计量经济学软件应用不到位， 大多数计量经济学教材中， 只给出计量模型的结果， 而结果是如何计算出来的却没有详细的介绍， 回归模型和计算结果之间的处理过程的缺失， 也就是软件应用的不到位， 增大了学生对这门课程的理解模糊性。

　　二、计量经济学课程性质分析

　　（一） 多学科知识理论交叉的性质。

　　计量经济学是经济理论、统计学、数学三者相结合的产物， 所以它既有文科的形式， 也兼具理科的性质， 这种特点一方面增加了计量经济学理论知识的丰富性， 另一方面也增加了学习难度， 并且也要求任课教师兼具经济学、数学和统计学等相关知识， 甚至还需要具有计算机操作的能力， 而目前具有这些能力的老师并不是很多， 有许多数学专业或是经济学专业出身的老师担任计量经济学的讲授往往会造成知识的片面性， 所以， 计量经济学教学水平和质量还有待于进一步的提高。

　　（二） 较强的实际应用性。

　　一般的数理经济学模型重视研究经济变量间的理论关系， 并用确定性的方程加以描述， 与此不同的是， 计量经济学重视研究经济变量间的定量关系， 用随机性的方程加以描述， 因此它具有很大的随机性。因为在计量经济学模型中引入了一个随机误差项μ。所以给计量经济模赋予了极大的魅力和实际应用性。

　　首先， 在实际生活中， 确定性的经济变量关系几乎是不存在的， 由于各种复杂的原因， 经济系统中总会带有一定的不确定性， 计量经济学模型中的随机干扰项或剩余项可以代表这种不确定性。其次， 由于收集变量伴随着经济成本， 必须在保证经济性的前提下取舍变量， 这时随机干扰项可以代表众多细小的影响因素， 既保证了模型的严谨性， 也带来了经济上的节约， 因此具有极强的实际应用性。

　　（三） 对专业性软件的依赖性。

　　由于计量经济学数字庞大、数据庞多的特点， 采用手工计算往往是不经济且不可行的， 在一元回归模型的情况下可能还可以应用EXCEL帮助计算， 然而对于多元， 尤其是两元以上的情况， 普通的表格软件显然不能满足要求， 所以计量经济学模型的估计和分析需要利用专业的计量经济分析软件配套计算机完成。比如STATA、SPSS、GAUSS、EVIEWS等专业软件， 尤其是EVIEWS软件， 由于其强大的数据处理功能和简便实用的特点， 已经成为计量经济学学习的首选， 所以在讲授计量经济学理论和检验方法的同时， 还应当适当地介绍一些计量经济软件。而要熟练地使用计量经济学软件， 仅仅依靠教师课堂教学是不足够的， 还需要学生课后进行练习。然而在实际的教学考核中， 大多数情况下并不将软件的应用能力作为考察的重点， 这就使得大多数情况下忽视软件应用能力， 进而降低计量经济学对于实际问题的实践解决能力。

　　三、计量经济学理论与实践问题解决方法

　　（一） 计量经济学理论问题解决方法。

　　由于计量经济学理论知识的复杂性和综合性， 为了更好地理解理论知识， 首先可以恰当处理整体知识与核心知识点之间的关系， 使在有限课时限制的情况下， 让同学了解更多的计量经济学知识， 为今后的学习和生活奠定理论基础， 其次， 在老师教学和学生学习的过程中， 应当杜绝片面的思想， 不能仅仅依靠数学或者经济学方面的知识， 要注重综合多元的思想， 真正把计量经济学学活， 真正发挥计量经济学独特的作用。

　　（二） 计量经济学实践问题解决方法。

　　计量经济学在实践方面遇到应用性不高的原因主要是数据建模问题和软件应用问题， 因为对收集数据方法和建模方法的不重视， 使得在开始应用计量经济学的时候就遇到了鸿沟， 如果不能有效的收集数据， 不能正确的设定模型， 即使检验方法烂熟于胸， 也难免会有"英雄无用武之地"的困境， 而对于软件的不重视也降低了计量经济学的实用性。

　　（三） 明确数据来源。

　　在实际的教学和学习中， 应当重视传授和学习收集数据的渠道和方法， 为实际应用提供支撑性条件。

　　（四） 重视传授建模方法。

　　由于大多数实际教学中直接给出问题模型， 造成了学生对于这一技能的空白， 填补这一方面的空白首先是引起重视， 然后结合现有的经济学理论， 分析模型设定形式的理由， 从而掌握方法。

　　（五） 加强实验教学、案例教学和软件教学。

　　首先应该把计量经济学的实验课程和软件应用技能化为重点考察对象， 从根本上上改变轻视实验课程和软件应用的现状， 其次加强案例教学， 使计量经济学更好的结合实际生活中的问题， 并增加教学的可操作性。

　　四、结语

　　?计量经济学的学习不应该只停留在理论层面， 而忽视实践作用， 处理好理论与实践中存在的问题， 才能真正在实际生活中发挥其应有的作用， 本文归纳整理了一些在计量经济学学习过程中存在的问题， 探讨了计量经济学的学科性质， 在此基础上， 提出了一些解决问题的方法， 希望能对今后的计量经济学学习产生一些影响。本文只是结合具体的教学内容进行了初步的探索， 许多深层次的理论和实践问题还有待于进一步的研究和探讨。

　　参考文献
　　[1]庞皓。计量经济学 （第三版） .科学出版社， 2014, 6.
　　[2]张晓峒。计量经济学基础 （第四版） .南开大学出版社， 2014-12-1.
　　[3]达摩达尔·N·古扎拉蒂。计量经济学基础·上册 （第五版） .中国人民大学出版社， 2011-6-1.
　　[4]杰弗里·M·伍德里奇。计量经济学导论·现代观点 （第五版） .中国人民大学出版社， 2015-5-1.
　　[5]李子奈， 潘文卿。计量经济学学习指南与练习 （第四版） .高等教育出版社， 2015-9-1.

计量经济学课程论文推荐范文10篇
相关内容推荐
相关标签：
返回：计量经济学论文
Copyright© 2006-2020 学术堂提供海量学术论文范文 版权所有