屈光不正大体分为近视、远视及散光。由于角膜屈光力(43D)占眼球屈光系统总屈光力的 70%左右,因此自上世纪 70 年代起兴起角膜屈光手术矫正屈光不正,先后经历了放射状角膜切开术(radialkeratotomy,RK)、准分子激光角膜切削术(photore-fractive keratectomy,PRK)、准分子激光角膜原位磨镶术(laser-assisted in situ keratomileusis,LASIK)、准分子激光上皮瓣下角膜磨镶术(laser-assisted ep-ithelial keratomileusis,LASEK)、Epi-LASIK(准分子激光机械法上皮瓣下角膜磨镶术)、飞秒激光制瓣LASIK、全飞秒激光手术等,至今已有 40 余年历史。
目前,数百万的角膜屈光手术后患者已进入中老年阶段,由于罹患白内障导致他们视力再次下降进而寻求白内障手术。然而,相比普通白内障患者而言,由于角膜屈光术后患者对术后视力期望值更高,而这些患者人工晶状体(intraocular lens, IOL)度数计算难度更大、准确性更低,因此角膜屈光术后白内障手术面临更多挑战。目前,有大量文献提出了关于这个难题的一些应对措施或变通方案,一些研究也对现行的计算方法作了深入分析。而且,我们还可以从互联网上获得帮助,如 Ken Hoffer医生的网站免费提供包含所有现用公式的电子数据表格下载;美国白内障与屈光手术学会(ASCRS)网站免费提供多种计算公式的在线计算服务;近日,亚太地区白内障与屈光手术医师协会(APACRS)推出了一款“屈光手术后生物测量计算”的在线计算器,使 Graham Barrett 的真正 K 值公式计算成为现实。面对以往文献中已提出的各种各样的屈光手术后 IOL 度数计算方法,本文不再重复汇总,而是主要分析问题出现的原因及如何用现有的计算方法去解决。
1 生物学测量
合并屈光不正尤其是高度近视眼被认为是特殊的眼睛,因为其涉及到 IOL 度数计算和患者对手术结果的高期望值,因此,我们应考虑到所有会影响到手术效果的潜在因素,比如测量误差。对于眼轴长的眼睛,尤其合并后巩膜葡萄肿的,眼轴测量误差是引起 IOL 度数计算偏差的最主要因素,应在最大程度上予以避免。光学测量法的应用使这一问题迎刃而解。因此,应对屈光手术后的患者使用光学法(或浸润式超声检查)测量眼轴,而非接触式超声检查。
2 角膜屈光手术后眼的特殊性
2.1 人工晶状体度数计算误差的来源 从本质上说,IOL 度数计算的误差主要来自三方面:角膜曲率半径测量误差、角膜屈光指数误差和 IOL 度数计算公式误差。
角膜屈光力是计算 IOL 度数的一个重要参数,但是目前还没有任何一种仪器可以直接测量角膜的屈光力。角膜曲率计或角膜地形图是通过测量角膜曲率半径从而推导出角膜的屈光力。由这两种仪器的测量原理可知,它们测量的并不是真正的视轴中央角膜曲率半径,而是视轴中央外 3 mm 左右区域的角膜曲率半径。LASIK 术后角膜激光切削区的周边部曲率半径较中央小,因此,推导出的角膜屈光力会比实际值偏大,导致选择的 IOL 度数偏低,患者术后出现远视漂移。这种角膜曲率半径的测量误差通常在近视性激光术后出现,但在远视性激光术后并不常见,目前仍缺乏相关的合理解释。
传统的角膜曲率计或角膜地形图是通过单纯测量角膜前表面曲率半径得出角膜屈光力,并没有考虑到角膜后表面的屈光性质。只有当角膜前、后表面曲率的比值固定时,才能由角膜前表面半径推出后表面半径或由角膜前表面屈光力推出后表面屈光力,从而避免产生角膜屈光指数误差。角膜前、后表面曲率之比称为角膜屈光指数(keratometer in-dex, KI),它可以通过以下公式把测量的角膜前表面曲率半径 Rant 转换为角膜屈光力 K:K=KI/Rant。
但是,激光角膜屈光手术后由于前表面曲率改变,而后表面曲率相对恒定,导致 KI 发生变化,不再遵从1.337 5(正常角膜的 KI 值),由此推算出来的 K 值也是不准确的。
此外,出现 IOL 度数计算误差另一来源是 IOL度数计算公式误差,典型代表是第三代 IOL 计算公式:Hoffer Q、Holladay-1、SRK/T,它们是通过 Ks 来推测有效晶体位置(effective lens position,ELP)。Ks即角膜曲率半径,它在一定程度上可代表眼前节的几何性质:角膜曲率扁平时则 ELP 小,角膜曲率陡时则 ELP 大。这个概念在 Fyodorov 和 Kolonko提出第一个 IOL 度数计算公式时就曾用到过。然而,屈光手术后角膜表面形状发生了变化,Ks 不再能代表眼前节的几何特性,近视准分子激光角膜切削术后角膜前表面曲率变平,导致错误地推算出偏小的ELP,使近视性屈光术后患者出现远视漂移;相反,远视准分子激光角膜切削术后角膜前表面曲率变陡,导致错误地推算出偏大的 ELP,使远视性屈光术后患者出现近视漂移。
2.2 误差的影响 如果不对这些产生误差的来源加以控制,其结果就是近视性屈光手术后出现远视漂移(可达 3D)以及远视性屈光手术后出现近视漂移。
角膜曲率半径测量误差取决于角膜曲率仪器的测量范围和激光切削区的范围。Haag-Streit 和Zeiss 角膜曲率计的传统测量范围分别为 3.4 mm 和2.5 mm。近年来随着现代准分子激光技术的发展,激光切削区面积在逐渐增加,大大降低了角膜曲率半径测量引起的误差,甚至只有零点几个屈光度。
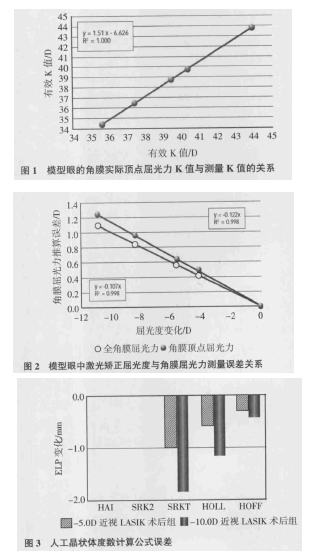
角膜屈光指数误差和 IOL 公式误差造成的影响可以通过模型眼计算加以评估。以往,近视模型眼是由 Gullstrand 模型眼拉长玻璃体长度并保持眼前节不变转化而来。准分子激光手术是通过改变角膜前表面曲率从而改变屈光状态。图 1~3 介绍了早期文献中提出的两种模型眼,并引入了另外两种屈光度在-4D 至-8D 左右的模型眼。图 1 显示的是模型眼的矫正曲率,可以由传统意义上的“测量”K值(=3 375/Rant,Rant 即角膜前表面曲率半径,mm)推导出有效(顶点屈光度)K 值。图 2 显示的是角膜屈光力误差与眼屈光度变化的函数。图 3 是关于不同的 IOL 度数计算公式误差引起的有效晶体位置改变。
图 1 是把近视性激光矫正术后患眼假设为正常眼,测量其角膜曲率,结果显示测量的角膜 K 值从 44D 变为 38D 时,实际上是从 44D 变为 37D。图2 是把目标屈光度的变化与角膜屈光力推算误差联系起来:对于 10D 的屈光变化,角膜屈光力推算误差介于 1.1D 与 1.3D 之间(取决于 10D 是总角膜屈光力还是顶点屈光力)。图 3 通过模拟 ELP 变化表示了 IOL 的计算公式误差。由基础光学可知 IOL 移位 1 mm 可分别在短眼轴眼(21 mm)、正常眼(23.5mm)和长眼轴眼(27 mm)引起 1.9D、1.2D 和 0.6D 的屈光改变。对于一个近视-10D 的患者采用 SRK/T公式,在图 3 中的模拟 ELP 改变将近 2 mm,相当于正常至长眼轴眼的屈光度改变了 1.2~2.4D。
总之,在屈光手术后 IOL 计算误差的来源中,角膜曲率半径测量误差的影响相对较小,与角膜曲率仪器测量范围和激光切削区范围相关。最大的误差来自角膜屈光指数和 IOL 计算公式误差,前者取决于需矫正的屈光不正度数,后者与使用的 IOL 计算公式有关。
因此,没有一种全能的方法可以解决屈光手术后 IOL 度数计算中存在的所有问题,包括测量仪器和使用的计算公式问题,更难的是需解决测量仪器的设计、激光切削区和计算公式的改变问题。所以未来的 IOL 度数计算公式会不同于现有的计算公式。
3 现有的解决方法及发展方向
鉴于上述多重误差的影响,在过去的 10 余年间,国际上推出了 20 余种 IOL 度数计算方法来改善角膜屈光术后 IOL 度数计算准确性。如计算屈光手术后有效角膜屈光力的公式,由于修正了角膜屈光指数误差,能精确计算有效角膜屈光力,可作为计算测量所得的总角膜屈光力或后顶点屈光力的直接函数(图 1),也可作为目标屈光力的函数(图 2)。此外,一些学者还通过与目标屈光力有直接或间接关系的参数变化达到计算有效屈光力的目的。
然而,仅仅得到矫正角膜屈光力值对屈光手术后 IOL 度数计算是远远不够的,因为 IOL 度数计算公式的误差仍然存在。解决这个问题的一种方法是Aramberri 的双 K 值矫正法,即用屈光术前的 K 值(或一个平均常数)计算有效 IOL 位置,另一种方法是选择不通过角膜曲率半径计算 ELP 的公式,如Shammas 公式和 Haigis 公式(它们仅需要矫正角膜屈光指数误差)。
此外,文献中还提出了得到 IOL 度数推荐值的许多方法,比如通过屈光手术前的数据计算得到目标屈光度的变化值或 IOL 度数的公式等。
这些解决方法的共同之处是都需要原始数据和/或附加测量和/或特殊的测量指标。然而,患者屈光术前原始参数往往因时间过于久远而遗失或即便有,参数的准确性也有待商榷(多年前角膜屈光术前角膜曲率测量仪器落后)。另外,屈光术后晶状体核硬化或近视性眼轴延长也导致那些需要原始数据的计算公式计算误差。考虑到以上缺陷,近年一些新的只需要白内障术前现有屈光参数的计算方法应运而生,例如 Haigis-L、Shammas、Wang-Koch-Maloney 方法等,研究显示这些改良公式较传统的临床病史法有更好的预测准确性。
Haigis使用 Haigis-L 公式对 278 只准分子激光手术后的患眼进行了 IOL 度数计算,其中有 222只眼术前为近视,56 只眼术前为远视。近视眼的预期平均计算误差为(-0.08±0.71)D,远视眼的预期平均计算误差为(-0.06±0.77)D,两组的误差绝对值中位数分别是 0.37D 和 0.40D。IOL 植入术后,近视组有 98.6%在预期值±2D 内,82.9%在预期值±1D内,59.9%在预期值±0.5D 内,而远视组的各比例分别为 96.4%、82.1%和 58.9%。Gale 等曾建议正常眼 IOL 植入术后应有 55%在预期屈光度±0.5D 以内,85%在预期屈光度±1.0D 以内。Haigis 的研究结果显示误差在±0.5D 内的比例高于 Gale 的建议值,误差在±1.0D 内的比例与 Gale 的要求大致相同。这说明经 Haigis-L 公式计算的屈光手术后患眼的屈光结果与正常眼相比,并无很大差异。
McCarthy 等对 LASIK/PRK 矫正近视术后行白内障手术的 173 只眼进行了研究,他们对比了 25对角膜屈光力调整公式和 IOL 度数计算公式组合的结果,发现有 5 对组合效果最佳,Masket/HofferQ、 临床经验法/Hoffer Q、Latkany Flat -K/SRK -T、Shammas 法和 Haigis-L 公式,这 5 种计算方法的平均预期屈光度误差分别为(-0.18±0.87)D、(-0.27±1.04)D、(-0.37 ±0.91)D、(-0.10 ±1.02)D、(-0.26 ±1.13)D;Wang 等用 ASCRS 角膜屈光术后 IOL 度数计算器对 72 只眼进行了研究,发现使用不参考原始数据的计算方法比使用术前 K 值的计算方法能得到更好的结果,他们研究结果显示 Shammas公式和 Haigis-L 公式的预期屈光度误差分别为(-0.24±0.81)D、(0.18±0.81)D。
笔者在 2012 年比较了 Holladay 人工晶状体(intraocular lens,IOL)度数计算软件(Holladay IOLConsultant Program,HICP) 及 ASCRS 角膜屈光术后IOL 度数计算软件中 8 种 IOL 度数计算方法(包括HolladayIIIOL -MasterK、HolladayIIFlatK、Wang -Koch -Maloney、Shammas、Haigis -L,ASCRS -Aver-age、ASCRS-Min 及 ASCRS-Max) 对无临床病史资料的近视准分子激光角膜屈光术后 IOL 度数计算准确性,显示 HolladayIIFlatK 方法 IOL 度数预测准确 性 更 优 于 Wang -Koch -Maloney、Shammas 及Haigis-L,由于研究例数(62 眼)有限,该研究结果仍有待进一步大宗数据支持。屈光手术后 IOL 度数的计算仍然是一项挑战。
本文详细分析了造成 IOL 度数计算偏差的来源(角膜曲率半径、角膜屈光指数和 IOL 计算公式误差),通过模型眼计算评估了各个来源误差对总体误差的影响,并总结了文献中提到的尽量减少现有计算方法误差的途径。新一代不依赖原始屈光参数的IOL 度数计算方法如 Haigis-L 公式、Shammas 法等已显示出更好的 IOL 度数计算准确性。相信随着这些不需要患者原始数据就能计算屈光手术后 IOL度数的方法的不断完善,不需原始数据便可对屈光手术眼进行 IOL 度数计算的时候指日可待。
参考文献:
[1] Klein B E, Klein R, Lee K E, et al. Incidence of age-related cataractover a 15-year interval the Beaver Dam Eye Study [J]. Ophthalmol-ogy, 2008,115(3):477
[2] Seitz B, Langenbucher A, Nguyen N X, et al. Underestimation of in-traocular lens power for cataract surgery after myopic photorefrac-tive keratectomy [J]. Ophthalmology, 1999,106(4):693
[3] Masket S, Masket S E. Simple regression formula for intraocular lenspower adjustment in eyes requiring cataract surgery after excimerlaser photoablation [J]. J Cataract Refract Surg, 2006,32(3):430
[4] Hoffer K J. Intraocular lens power calculation after previous laser re-fractive surgery [J]. J Cataract Refract Surg, 2009,35(4):759
[5] Naseri A, McLeod S D. Cataract surgery after refractive surgery [J].Curr Opin Ophthalmol, 2010,21(1):35
[6] Wang L, Hill W E, Koch D D. Evaluation of intraocular lens powerprediction methods using the American Society of Cataract and Re-fractive Surgeons Post-Keratorefractive Intraocular Lens Power Cal-culator [J]. J Cataract Refract Surg, 2010,36(9):1466
[7] Hoffer/Savini tool. Available at: (accessed 4September 2011)
[8] ASCRS Post -refractive surgery IOL calculator. Available at: (accessed 4 September 2011)
[9] Biometry calculation post refractive surgery. Available at: www.a-pacrs.org (accessed 4 September 2011)
[10] Graham B. True-K formula[R]. In: ASCRS Eye World Meeting Re -porter, under“Advanced phaco techniques”, 1 July 2008
[11] Fyodorov S N, Kolonko A I. Estimation of optical power of theintraocular lens[J]. Vestnik Oftalmologic (Moscow), 1967,4:27
[12] Savini G, Carbonelli M, Barboni P, et al. Clinical relevance of radiusof curvature error in corneal power measurements after excimer lasersurgery [J]. J Cataract Refract Surg, 2010,36(1):82
[13] Haigis W. Intraocular lens calculation after refractive surgery [J].European Ophthalmic Review, 2012,6(1):21
[14] Koch D, Wang I. Calculating IOL power in eyes that have had re-fractive surgery [J]. J Cataract Refract Surg, 2003,29(11):2039
[15] Jin H, Holzer M P, Rabsilber T, et al. Intraocular lens power calcu-lation after laser refractive surgery[J]. J Cataract Refract Surg, 2010,36(1):87
[16] Savini G, Barboni P, Zanini M. Intraocular lens power calculationafter myopic refractive surgery. Theoretical comparison of differentmethods [J]. Ophthalmology, 2006,113(8):1271
[17] Geggel H. Pachymetric ratio no-history method for intraocular lenspower adjustment after excimer laser refractive surgery[J]. Ophthal-mology, 2009,116(6): 1057
[18] Aramberri J. Intraocular lens power calculation after corneal refrac -tive surgery: double K method[J]. J Cataract Refract Surg, 2003,29(11):2063
[19] Shammas H J, Shammas M. No -history method of intraocular lenspower calculation for cataract surgery after myopic laser in situ ker-atomileusis [J]. J Cataract Refract Surg, 2007,33(1):31
[20] Haigis W. Intraocular lens calculation after refractive surgery formyopia: the Haigis-L formula[J]. J Cataract Refract Surg, 2008,34(10):1658
[21] Diehl J W, Yu F, Olson M D, et al. Intraocular lens power adjust-ment nomogram after laser in situ keratomileusis [J]. J Cataract Re-fract Surg, 2009,35(9):1587
[22] Awwad S T, Kelley P S, Bowman R W, et al. Corneal refractive pow-er estimation and intraocular lens calculation after hyperopic LASIK[J]. Ophthalmology, 2009,116(3): 393
[23] Feiz V, Mannis M, Garcia -Ferrer F, et al. Intraocular lens powercalculation after laser in situ keratomileusis for myopia and hyper-opia: a standardized approach[J]. Cornea, 2001,20(8):792
[24] Walter K A, Gagnon M R, Hoopes P C, et al. Accurate intraocularlens power calculation after myopic laser in situ keratomileusis by-passing corneal power [J]. J Cataract Refract Surg, 2006,32(3):425
[25] Kalyani S D, Kim A, Ladas J G. Intraocular lens power calculationafter corneal refractive surgery[J]. Curr Opin Ophthalmol, 2008,19(4):357
[26] Wang L, Booth M A, Koch D D. Comparison of intraocular lens pow-er calculation methods in eyes that have undergone LASIK [J]. Oph-thalmology, 2004,111(10):1825
[27] Olsen T. Calculation of intraocular lens power: a review[J]. ActaOphthal Scand, 2007, 85(5):472
[28] Gale R P, Saldana M, Johnston R L, et al. Benchmark standards forrefractive outcomes after NHS cataract surgery[J]. Eye, 2009,23(1):149
[29] McCarthy M, Gavanski G M, Paton K E, et al. Intraocular lens powercalculations after myopic laser refractive surgery: a comparison ofmethods in 173 eyes [J]. Ophthalmology, 2011,118(5):940
[30] Yang R, Yeh A, George M R, et al. Comparison of intraocular lenspower calculation methods after myopic laser refractive surgerywithout previous refractive surgery data [J]. J Cataract Refract Surg,2013,39(9): 1327