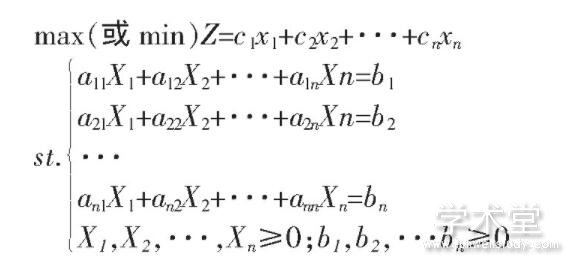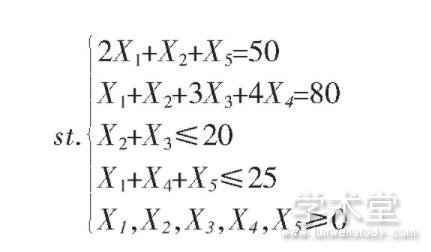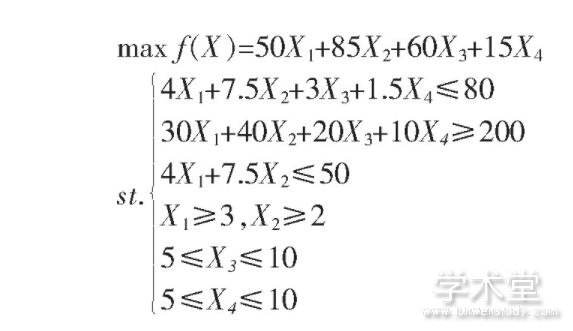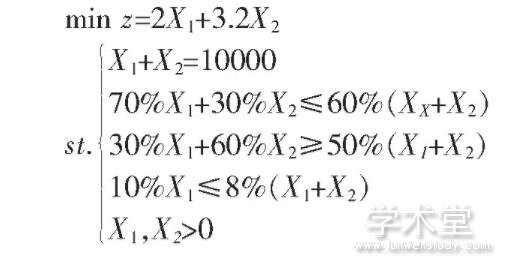数学与生活论文第五篇:实际生活中线性规划数学工具的使用分析
摘要:线性规划是一种充分利用有限资源达到最优化的数学方法,在满足某些约束条件下,求出目标函数的最优解,该文首先阐述了线性规划的定义,然后对线性规划在实际生产生活中的应用进行了具体介绍,如合理下料问题、投资问题、集合料问题用线性规划选择了最优方案。
关键词:线性规划; 实际生活; 应用;
On the Application of Linear Programming in Practical Life
CAO Yaqun
Anhui Technical College of Water Resources and Hydroelectric Power
Abstract:Linear programming is a mathematical method to make full use of limited resources to achieve optimization. Under certain constraints, the optimal solution of objective function is obtained. This paper first expounds the definition of linear programming, and then introduces the application of linear programming in practical production and life.For example, the problem of reasonable cutting stock, investment and transportation are optimized by linear programming.
1 什么是线性规划
线性规划是运筹学的重要分支,是合理分配及利用有限资源,以取得最佳经济效益的一种优化方法。它采取的是在一系列条件约束下,获得最优值的数学理论[1]。线性规划是一种数学规划方法,满足约束条件下,让目标函数取得最优值。它要解决的问题通常约束条件及目标函数是线性关系,约束条件是不等式或者等式,目标函数取极值。线性规划在管理学、建筑学、经济学等领域都有着广泛的应用,例如:下料问题、库存问题、运输问题等。线性规划都有一定的形式,标准形式如下:
2 线性规划在实际生活中的应用
在我们的实际生活中,可以利用线性规划解决很多问题以减少人们的工作量、节约经费,提高工作效率[2]。生活中一些常见问题,比如两种不同型号材料的配比问题、话费选用套餐问题等,都可以用线性规划这种统筹方法找到最优解。下面,我们就以生活中某些常见问题为例,说明线性规划在实际生活中的应用。
2.1 线性规划在合理下料问题中的应用
合理下料问题是线性规划模型中的典型问题,建筑施工中,需要大量的各种各样的原材料,比如:钢材、木材、铝合金、砂、石、塑钢等建筑材料,而生产厂家只能提供一定规格的原材料,实际施工时要裁减才能得到所需要的规格,这样必然会产生残料,造成一定的损失和浪费,所以,合理下料,尽量减少产生残料,这让建筑企业能够减少成本投入,获得更高的经济效益[3]。下面,选用一个例子来说明线性规划在下料问题中的实际应用。
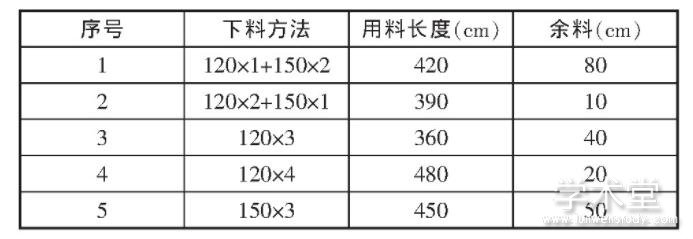
问题:要把20根4 m长和25根5 m长的同规格钢材,截成1.5 m的50根,1.2 m的80根,如何下料废料最少?(所有下料方法见表1)
表1 下料方法
解:设用以上五种方法分别各用X1,X2,X3,X4,X5,次,则min f(X)=80X1+10X2+40X3+20X4+50X4
运用LIND0软件,解得X1=0,X2=20,X3=0,X4=10,X5=10,即方法2用20次,方法4用10次,方法5用10次,废料最少为900 cm。
2.2 线性规划在广告投放问题中的应用
如今,随着人民生活水平的不断提高,几乎每家都有电视,电视的普及率已经相当高了。尤其是目前手机、电脑等电子产品的普及更是让人们感受到科技的力量。鉴于此,很多商家将目光投向了各种应用媒体平台的广告时段,目的就是增加自己的产品在人们视线中的出现频率。各个广告投资商需要根据具体情况,弄清楚各个媒体平台播放广告的时间及所需资金,以便获得更大的利润[4]。接下来我们用实际生活中的例子进行举例分析。
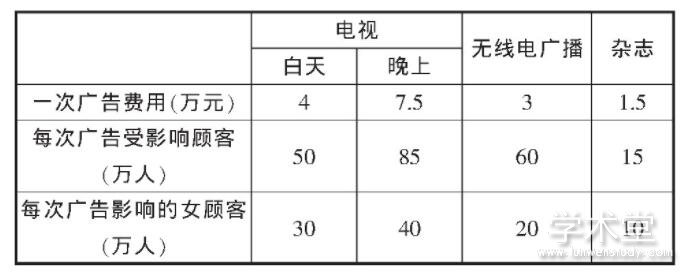
问题:某商家在投入资金不超过80万元的条件下,需要保证至少有200万女性观众观看广告,其中在电视台投入的广告费用不超过50万元,电视台在白天至少播出3次,在晚上至少播出2次,无线电广播和杂志的广告播放次数均不低于5次且不超过10次,广告市场调查结果如表2所示,问要想获得理想的广告效果应该如何安排播放次数。
表2 广告市场调查结果
解:设电视台的广告在白天的播放次数为X1次,晚间的播放次数为X2,无线电广播播放X3次,杂志的广告刊登为X4次。则:
运用LIND0软件,解得X1=3,X2=3,X3=10,X4=10,此时,总观看人数是1 155万人,女性观看人数是510万人,总支出是79.5万元。
2.3 在集合料问题中应用
解决集合料问题必须满足一定的条件,如种类、含量等,用数学语言表达各个条件,就是线性规划模型中的约束条件,要求所用的运输费用最省,用数学语言表达,就是线性规划模型中的目标函数,在集合料问题中,有很多不同方案被选择,优化目的就是从众多方案中选出一个最优方案[5]。
问题:某个筑路工地铺设道路基层,需要10 000 m3集合料,准备从两个弃土堆取混合料,已知弃土堆A的材料成分为:砾石含量70%,砂含量30%,弃土堆B的材料成分为:砾石含量30%,砂含量60%,粘土含量10%,集合料的成分含量要求为:砾石含量60%,砂含量50%,粘土含量8%。从弃土堆A取料的装载运输费为2元/m3,从弃土堆B取料的装载运输费为3.2元/m3。问应如何取料才能使总的运输费用最少?
解:设从弃土堆A、B取料数量分别为X1、X2m3,则:
解得:X1=3 333 m3,X2=6 667 m3即从弃土堆A取料3 333 m3,从弃土堆B取料6 667 m3,这样配料装卸运输费用最少为28 000元。
3 结语
线性规划是有力的数学工具,它的重要目标就是规划出各种“最优”,即如何用最佳的方式分配有限的资源,以获得最佳经济效益,如施工建筑下料问题中节约了材料,尽量减少残料的发生,合理下料,投资广告问题中获得预期的广告效果,集合料问题中如何取料运输费用最少,线性规划在诸如这些生活中的具体应用还有很多很多。
参考文献
[1]曹亚群,朱俊.线性规划在物流工程中的应用[J].宿州学院学报,2010,11(25):30-31.
[2]王茹,黄亚辉.线性规划在实际生产生活中的应用[J].科技创新导报,2018(9):155-156.
[3]赵云翔,陈建锋.线性规划在施工下料中的应用[J].杨凌职业技术学院学报,2004,3(1):24-25.
[4]杨晓波.线性规划在物流管理中的应用[J].产业与科技论坛,2014,13(21):57-58.
[5]陈广斌.线性规划在道路交通集合料中的应用[J].科技信息,2010(7):116.
点击查看>>数学与生活论文(精选论文8篇)其他文章