期货交易所与监管层多主体博弈模型的构建

　　一、引言

　　多层次资本市场体系日臻健全，随着期货市场创新步伐加快，市场功能也得到了进一步的发挥，各交易所之间的竞争也更加激烈，争取新品种上市交易就成了交易所新的经济增长点。在激烈的竞争中，中国证监会 （以下简称监管层） 作为品种资源的拥有者，不得不面对多家交易所采取不同的策略，期货交易所与监管层间的信息博弈也就在所难免。若干年来，学者们在研究信息博弈过程中，不断提出诸如子博弈精炼纳什均衡[1]、联盟博弈[2]、信号博弈[3]等新的方法和思路，部分学者针对多主体间的因果关系建立了各种博弈模型，使得策略均衡问题得以初步解决，信息博弈的研究不断深入[4-6]。近几年来，围绕期货市场信息博弈中的多主体、多层次和多阶段重复、混合博弈等问题，学者们开展了多方面的探讨。张玉智、赵佳琪(2014)以期货和现货两个市场的微观和宏观两个层次为背景，设计了内核信息流动双层多主体博弈模型，分析宏观博弈战略，为监管层提供决策依据。罗剑(2008)曾就期货交易者之间的演化博弈、机构间合作的演化博弈以及期货监管部门监管主导和期货法治秩序演化机制等问题进行了深入讨论[7]。张玉智、曹凤岐(2009)建立监管层与交易所、监管层与期货公司、监管层与投资者、期货公司与投资者以及投资者之间的信息博弈模型分析期货市场过度投机动因。刘洋(2010)界定了农产品期货市场信息博弈当事人参与信息流动的角色，构建出农产品期货市场监管层与期货交易所信息博弈模型[8]。翁东东、陈春春、孔德议(2011)从演化博弈理论的视角论证了期货市场联合操纵行为演化的方向和路径。刘敬伟、蒲勇健(2012)认为建立博弈联盟以集中把握资金和信息对于期货市场多空双方的博弈策略至关重要[9]。张瑞(2012)构建动态博弈模型，提出由于期货公司之间存在综合实力及市场策略等横向差别，导致手续费比例存在较大差异。张玉智、张秀莲(2013)将期货市场信息生态环境分为开放、收敛和真空三类，并从信息生态环境优化视角解析了期货市场组织者和监管层间博弈演化问题。

　　从文献成果来看，建立的期货市场博弈模型多只是针对不同参与主体展开相关研究，尚未涉及到期货交易品种这一稀缺资源在作为分配者的监管层与作为品种资源争夺者的交易所之间产生的多主体博弈问题。因此，构建基于交易品种竞争的期货交易所与监管层的多主体博弈模型就十分必要。该博弈模型可以进一步解释资源有限条件下一个分配者与多个争取者之间的多主体博弈，因此具有普遍的分析意义。

　　二、基于品种竞争的交易所与监管层多主体信息博弈的产生

　　根据 《期货交易管理条例》 和 《期货交易所管理办法》 的有关规定，期货交易所开发新品种，需经申请后进行长期可行性论证，并报监管层审核，获批复后才可有条件上市交易。监管层是品种资源的所有者，交易所是品种资源的使用者。如果仅有一家交易所，那么监管层和交易所间的目标就是一致的，即他们的目标都是上市新品种的利用率最大化，交易所获得最大收益，整个期货行业也获得最大收益，不存在利益的外部溢出问题。但是，目前我国有中国金融期货交易所、上海期货交易所、大连商品交易所和郑州商品交易所，除中国金融期货交易所专营金融期货外，当其余三家交易所并行争取新交易品种时，就存在一个将有限的品种资源分配到三家交易所的问题。

　　监管层的职责就是将有限的资源在三家交易所之间合理分配，实现整个期货行业的收益最大化；而交易所的目标则是争取到足够的品种资源，使本交易所的收益最大化。但是在品种资源有限的条件下，整个期货行业的收益最大和交易所的收益最大往往会出现冲突。为了实现整个期货行业收益最大化，有时需要将品种资源在多个交易所间进行不均衡分配，于是产生了基于交易品种竞争的期货交易所与监管层之间的博弈。

　　博弈论是研究决策主体的行为发生直接相互作用时的决策及其均衡问题[10]。在一个博弈过程中，博弈要素主要包括参与人、策略空间、信息、支付函数、均衡五个方面。文章构建的信息博弈模型中，参与人是指决策主体和策略制定者，包括监管层和三家期货交易所，共四个参与人；策略空间是指监管层和交易所可能采取的全部决策的集合，是参与人进行博弈的工具和手段；信息是指监管层及交易所掌握的对手的策略选择及可能获得的收益信息等知识；支付函数是指监管层与交易所实施策略后获得的利益和效用水平；均衡是指所有参与人的最优策略组合。博弈按照参与人决策和行动的先后顺序可以分为静态博弈和动态博弈，参与人同时决策并行动的称为静态博弈，参与人先后、依次决策并行动的称为动态博弈；博弈按照参与人对对手的策略空间、信息及支付函数的了解程度可以分为完全信息博弈和不完全信息博弈。由于文章假设信息资源可以共享，博弈主体可以调整博弈策略，由监管层先确定品种资源的分配方案后，各家交易所再采取行动，每个参与人都可以选择自己的最优策略，所有参与人选择的策略构成策略组合，且没有任何参与人有积极性打破这种均衡，因此构建的是完全信息动态博弈模型，即子博弈精炼纳什均衡。

　　三、交易所与监管层多主体博弈模型的构建
　　
　　以往研究文献关于多主体博弈的研究中鲜有涉及到基于资源的有限性构建的一个分配者与多个争取者之间的多主体博弈问题。马骏(1995)建立了中央政府和地方政府间财政关系的动态博弈模型[11]。文章参考该模型的设计过程，以交易所和监管层为例，构建了期货交易所与监管层之间的多主体博弈模型，并对这种类型的多方主体博弈进行定性和定量分析。

　　1. 基本假设

　　在期货监管业务中，通常由监管层负责上市品种资源调配，多个交易所分别负责本交易所上市品种的争取。为方便分析，文章提出以下假设条件。

　　假设条件 1：在期货市场只有监管层负责品种资源调配，有两个分别负责市场 1 和市场 2 的交易所 X 和交易所 Y。这样就可以构建出一个基于品种资源有限条件的一个分配者和两个争夺者之间的三方博弈模型。在该模型中包括一个监管层与两家交易所共三个参与人，三个参与人对期货市场的信息和对手方可能选择的策略和获得的效用等信息都了解。监管层的目标是将有限的品种资源总量 N，在市场 1 和市场 2 之间进行合理分配，实现整个期货行业的总收益最大化；而交易所的目标则是争取到足够的品种资源，实现本交易所收益最大化。由于是监管层先确定品种资源的分配方案，交易所再进行策略选择，因此属于完全信息动态博弈。

　　假设条件 2：品种资源总量不能够充分满足市场 1 和市场 2同时获得最大收益，即在一个市场的品种资源需要得到充分满足的条件下，另外一个市场的品种资源需求不能够被充分满足。

　　只有满足该假设条件，才会存在两家交易所和监管层三者之间的博弈。

　　假设条件 3：交易所 X 和交易所 Y 都是“理性经济人”，即当本交易所的品种资源充分满足的条件下均会采取合作策略。各家交易所明确在本交易所品种资源不能充分满足的条件下，如果选择不合作的方式可能会争取到更多的品种。若所有的交易所都采用合作策略，就只存在监管层的策略选择问题。

　　只有满足该假设条件，才存在交易所与监管层之间的博弈。

　　假设条件 4：无论哪个市场获得的收益都属于整个期货行业的总收益，所以对于交易所要求本交易所品种资源获得最大收益的动机，就可以解释为，交易所可以按照一定量的比率获得市场收益份额。

　　2. 模型构建

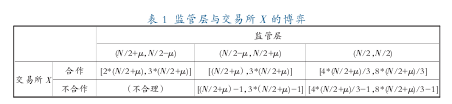
　　文章假定监管层有 N 个单位的品种资源总量，而每个交易所需要获得的能够充分满足的品种资源总量设为 N/2+μ （μ 为固定常量），不能够充分满足交易所需要的品种资源总量设为N/2-μ，为简单起见，监管层可以选择三种分配策略：(N/2+μ，N/2-μ)、(N/2-μ，N/2+μ)以及(N/2，N/2)，括号内分别表示分给交易所 X 和交易所 Y 的品种资源量。然而面对监管层的分配策略，交易所有两种策略，即积极合作与消极接受，也可以合作与不合作。

　　假定监管层认为两个交易所都采用合作策略，那么当每个市场得到 N/2+μ 个单位的品种资源时，市场的收益为 2 倍品种资源投入，即 2*(N/2+μ)。而品种资源不能充分满足交易所需求的条件下，资源投入的收益率下降，当每个市场得到 N/2-μ 个单位的品种资源时，市场的收益为充分满足条件下市场收益的1/2，即 2*(N/2+μ)/2=(N/2+μ)；当每个市场得到 N/2 个单位的品种资源时，市场的收益为充分满足条件下市场收益的 2/3，即4*(N/2+μ)/3。但是，若监管层采用(N/2+μ，N/2-μ)或(N/2-μ，N/2+μ)分配策略，得到 N/2-μ 个单位品种资源的交易所可能会采取不合作策略，对应的市场获得的收益可能会比预测得少，假定为选择合作策略下获得的市场收益 -1。

　　假设无论监管层选择何种策略，交易所 Y 都采取合作策略，因此可以构造出如表 1 所示的博弈模型。

　　3. 博弈分析

　　对于监管层来说，策略(N/2，N/2)不是一个理性的选择。此时两个市场品种资源的供给都不能充分满足，所以两个市场的收益率都很低，整个期货行业的总收益低于将品种资源充足供给一个市场所能带来的收益。所以，监管层只需要在(N/2+μ，N/2-μ)或(N/2-μ，N/2+μ)这两种策略中做出选择，这两种选择对于监管层来说是没有区别的。但对于交易所 X 来说(N/2+μ，N/2-μ)显然优于(N/2-μ，N/2+μ)，所以对于监管层以及交易所 X和交易所 Y 这三个参与人来说，此时的纳什均衡就是[(N/2+μ，N/2-μ)，合作，合作]。

　　同理，无论监管层选择何种策略，交易所 X 都采取合作策略时，对交易所 Y 来说，博弈的纳什均衡就是[(N/2-μ，N/2+μ)，合作，合作]。

　　但是，当交易所 X 获得了 N/2+μ 个单位的品种资源，而交易所 Y 只能获得 N/2-μ 个单位的品种资源时，交易所 Y 可以采取不合作策略，那么监管层就得不到预期的 3*(N/2+μ)个单位的收益，这将成为交易所 Y 要求得到更多品种资源的砝码。

　　四、交易品种资源的合理配置

　　在实际期货市场的监管和运作过程中，期货交易品种资源的配置对交易所乃至整个期货行业收益的影响要更加复杂，如何在资源有限的情况下对期货交易品种进行合理配置，是期货交易所和监管层都应关注的一个问题。

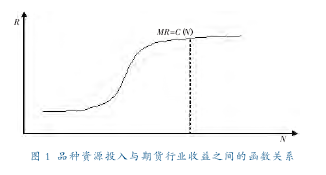
　　假设监管层对期货市场的所有投入可以只用一种资源即交易品种来表示，依据“边际效用递减规律”，在实际期货市场的监管和运作过程中，期货交易品种资源的配置对交易所、乃至整个期货行业收益的影响要更加复杂，如何在资源有限的情况下对期货交易品种进行合理配置，是期货交易所和监管层都应关注的一个问题。随着交易品种资源投入量 N 的增加，资源投入的收益 R 是变化的，资源投入的边际收益率 MR 先增加后减少。交易品种资源投入量 N 与期货行业收益 R 之间的函数关系如图 1 所示。

　　设交易所 X 所得到的品种资源总量为 NA，则该交易所的收益 RA是 NA的函数 CA(NA)，即RA=CA(NA)；交易所 Y 所得到的交易品种资源总量是 NB，其收益 RB是 NB的函数 CB(NB)，即 RB=CB(NB)；期货行业的总收益则应为 RAB=RA+RB=CA(NA)+CB(NB)。

　　考虑到实际中每家交易所均有要求本所收益实现最大化的动机以及采取[合作，合作]策略的积极性，上述期货市场总收益公式过于理论化，这里文章借鉴马骏中央与地方财政关系政策模型中的收益比例设定，令交易所 X 和交易所 Y 的收益按照固定的比例 rA和 rB(0燮rA，rB燮1)归整个期货行业所有 （实际中各交易所的收益都是属于整个期货行业的，可以假定 rA和 rB的值相当大，接近于 1）。

　　基于此，整个期货行业的收益可以用以下数学公式表示：RAB=rA×NA×CA(NA)+rB×NB×CB(NB) (1)同时，监管层必须保证每个交易所都能安全驾驭新增品种风险，不能由于某一个交易所不能驾驭新增交易品种的市场风险从而对整个期货行业造成损失。所以每家交易所的交易品种资源分配必须大于各自的一个下限 N*A和 N*B，即 NA叟N*A，NB叟N*B并且各交易所分配的交易品种资源之和必须要小于交易品种资源的总量 N0。因此，可以得到约束条件：

　　NA+NB燮N0(2)NA叟N*A(3)NB叟N*B(4)根据公式(1)构造整个期货行业收益的拉格朗日函数：R*AB=rA×NA×CA(NA)+rB×NB×CB(NB)+λ(NA+NB-N0) (5)其中，λ 为固定常数，由此可以得到整个期货行业收益最大化的一阶条件为：

　　rA[CA(NA)+NA×CA'(NA)]+λ=0 (6)rB[CB(NB)+NB×CB'(NB)]+λ=0 (7)NA+NB-N0=0 (8)公式(6)和(7)去掉λ得到：rA[CA(NA)+NA×CA'(NA)]=rB[CB(NB)+NB×CB'(NB)] (9)由于假定 rA和 rB接近于 1，因此可以直接设 rA=1，rB=1，可以得到：CA(NA)+NA×CA'(NA)=CB(NB)+NB×CB'(NB) (10)公式(8)实际上是期货交易品种资源总量的约束条件：NA+NB=N0(11)若能得到交易所 X 和交易所 Y 的交易品种资源投入市场后的收益函数 CA(NA)、CB(NB)及各交易所的 rA和 rB，则由公式(10)和公式(11)就可以求出交易品种资源最佳分配解。

　　五、结论

　　目前三家期货交易所中大连商品期货交易所上市交易品种16 种，上海期货交易所上市交易品种 12 种，郑州商品交易所上市交易品种 15 种。2014 年 5 月 8 日出台的 《国务院关于进一步促进资本市场健康发展的若干意见》 （国发[2014]17 号）中提出健全多层次资本市场体系，以提升产业服务能力和配合资源性产品价格形成机制改革为重点推进商品期货市场建设，陆续推出大宗资源性产品期货品种，开发商品期权、商品指数、碳排放权交易工具，增强期货市场服务实体经济的能力，可见，今后商品期货市场建设的重点将主要集中在新品种的开发与交易上，各家交易所为保证自身收益最大化，必将展开激烈的品种资源争夺战。而作为品种资源分配者的监管层则应在考虑期货品种上市效率的前提下，引导各期货交易所通过竞争寻找优势品种，实现期货品种资源的有效配置，满足实体经济的个性化需求，提高期货行业的整体收益。

　　文章设计了基于交易品种竞争的期货交易所与监管层间的多主体博弈模型，该模型将博弈理论引入了多层次资本市场体系的监管中来，给出了多市场监管中上市交易品种资源分配问题的一种解决方案。虽然该模型只是针对单一品种资源的竞争问题进行分析，没有涉及到多种资源间的替代关系，模型存在有待完善之处，但对资源有限条件下，一个分配者与多个争取者间的多主体博弈问题的分析做出了有益尝试。近年来，地方政府纷纷向中央政府争取资源，高等院校纷纷向有关机构争取科研项目，中小企业纷纷向主管部门争取补贴经费，这都涉及到资源有限情况下一个分配者与多个争取者之间的多主体博弈。该模型的构建为资源拥有者和资源分配者之间的博弈提供了最佳策略选择模型，具有普遍的研究意义。