日本的货币政策与经济周期的相关性分析

　　3 泡沫经济危机的货币政策因素分析

　　3.1 日本的货币政策与经济周期的相关性分析

　　本节用定性分析与定量分析相结合的方法，来考察日本货币政策的变化与经济周期波动之间所存在的关系，为研究泡沫经济危机的成因奠定基础。

　　3.1.1 定性分析

　　本小节主要考察日本政府在“广场协议”后历次实行的货币政策是顺经济周期--在经济繁荣（衰退）时实行宽松（紧缩）的货币政策，还是逆经济周期--在经济繁荣（衰退）时实行紧缩（宽松）的货币政策。

　　从1983年10月开始，日本银行为应对日元升值的压力，一直保持着5.0%的再贴现率，以维持较宽松的金融环境，推动了经济的快速增长。但1985年9月“广场协议”的签订引起日元剧烈升值，经济开始下滑，日本政府实行了扩张性的货币政策，从1986年1月至12月连续四次降低再贴现率，由5.0%降至3.0%,以维持日元汇率稳定并刺激国内需求。1986年是第6次经济周期的萧条期，而宽松的货币政策显然是逆经济周期的，该政策使日本经济从1986年年底开始复苏。

　　1987年已经进入第7次经济周期的复苏阶段，而日本银行于2月再次降低再贴现率，从3.0%降至2.5%,这是顺经济周期的货币政策，经济开始加速高涨，这也是泡沫经济的形成时期。受“黑色星期一”事件的影响，本打算从1987年11月逐步提高利率的日本银行将2.5%的超低再贴现率一直保持到1989年4月。1987年末到1988年末是第7次经济周期繁荣时期，此期间的货币政策仍然是宽松的，是顺经济周期的，这便推动了泡沫经济的迅速膨胀。

　　1989年初，日本经济开始进入第7次周期的衰退阶段，此时，由于经济泡沫化问题越来越严重，日本政府开始控制泡沫，大幅度紧缩货币政策，将再贴现率连续五次上调，从2.5%调至1990年8月6.0%的高点。此阶段紧缩的货币政策是顺经济周期的，该政策的实施直接刺破了高涨的泡沫，加速了经济周期的衰退。

　　从1991年开始，经济增长速度急剧下滑，1991年到1993年仍然处于第7次经济周期的衰退和萧条时期。而1991年7月起，日本政府为了恢复经济，扩大内需，再次放松银根，五次大幅度下调再贴现率，由6.0%下调至1993年9月的1.75%水平。显然该货币政策是逆经济周期的，但此时已无法挽救泡沫经济崩溃所带来的衰退。日本从此进入了长期低增长率阶段。

　　1.75%的再贴现率水平一直维持到1995年3月，虽然日本经济开始回升，但日元汇率仍不断降低，于是，日本银行再度连续两次降低再贴现率，并将再贴现率长期保持在0.5%的水平。此次扩张的货币政策顺应了第8次经济周期的扩张时期。1997年之后，经济转入收缩期，日本银行将隔夜拆借利率下调到0.25%,此时的货币政策是逆经济周期的。

　　由于经济出现负增长以及不良债权问题的严重性，日本银行开始实施零利率政策。隔夜拆借利率经过两次下调，降至1999年3月的0.03%,这表示金融市场中实际利率为零。零利率政策一直持续到2000年8月，此阶段处于第9次经济周期的扩张时期，该政策是顺经济周期的。

　　2000年8月，在经济回暖的情况下，日本银行调高了隔夜拆借利率，从0.03%调至0.35%,该货币政策是逆经济周期的。2001年，日本经济转入第9次周期的衰退期，日本银行又开始放松银根，将再贴现率降至0.35%,同时，将隔夜拆借利率降至0.15%,此时的政策是逆经济周期的。

　　在此之后，日本银行通过公开市场操作等措施继续实施数量宽松的货币政策。第10次经济周期的扩张期和收缩期对应了该宽松政策的顺周期性和逆周期性。2006年日本经济回暖，进入第11次经济周期的扩张期，日本银行于3月开始实施的紧缩的货币政策显然是逆经济周期的。

　　“广场协议”后，日本银行除了在第9次经济周期的衰退时期实行了紧缩的货币政策，其他时期主要采用了扩张性的货币政策，长时期维持着较低的利率。表3-1显示了各时期货币政策的顺或逆周期性。

　　3.1.2 定量分析

　　3.1.2.1 模型介绍和变量选取

　　本小节拟用向量自回归（VAR）模型，来分析日本货币政策变化与经济周期波动的相关性。VAR模型将多个方程联立到一起，在每个方程中，内生变量都对模型中所有内生变量的滞后值进行回归，以此考察各内生变量之间的动态关系。

　　含有个 N 变量滞后k期的VAR模型可表示为：

　　模型中方程右侧的每一项都是内生变量的滞后项，它们与tu 是渐近不相关的，因此，用最小二乘法估计每个方程所得到的参数估计值均具有一致性。

　　建立VAR模型不必依据严格的经济理论，只需正确选择有相互关系的变量并确定最优的滞后期。最优滞后期的选择通常依据LR（似然比）检验、AIC信息准则和SC准则三种方法共同来确定。其确定原则是：选择同时使AIC值和SC值最小的滞后阶数，否则，参照LR检验值来确定最优滞后期。所建立的VAR模型必须是稳定的才可以使用，其稳定性要求AR特征多项式的k   N个特征根的倒数必须全部位于单位圆内。

　　本文用贷款利率、货币供应量和GDP这三个经济变量来建立VAR模型，贷款利率（用LR表示）和货币供应量（用M表示）作为货币政策的代表量，GDP（用G表示）作为经济周期的代表量。数据来源于世界银行所公布的1960年到2010年之间的年度数据，详细数据见附录。

　　由于货币供应量和GDP的数据位数过大，所以将时间序列M和G先进行对数化操作，得到序列LNM和LNG.

　　3.1.2.2 单位根检验

　　建立模型之前一般都要对所选取的时间序列进行单位根检验，判断其是否平稳。本文采用ADF检验方法来检验LR、LNM、LNG三个时间序列变量的平稳性。

　　表3-2给出了用EViews软件操作得出的检验结果：

　　从表中可以看出，三个变量的ADF统计量在1%、5%以及10%的显着水平下，均大于临界值，接受了存在单位根的原假设，说明三个时间序列都是不平稳的。

　　对于不平稳的时间序列，一般会通过差分变换来使其满足平稳性。因此，本文分别对LR、LNM、LNG三个序列取一阶差分，得到三个差分序列DLR、DLNM、DLNG,然后检验这三个差分序列的平稳性，ADF检验结果如表3-3所示：

　　从表中的数据可知，一阶差分得到的三个新变量的ADF统计量在1%、5%以及10%的显着水平下，都小于临界值，存在单位根的原假设被拒绝，可见，差分序列DLR、DLNM、DLNG是平稳的。也就是说，LR、LNM、LNG这三个变量都是一阶单整的。

　　3.1.2.3 协整检验

　　几个非平稳的时间序列的线性组合可能是平稳的，也就是说，这几个变量之间可能存在协整关系。

　　从表中可以看出，在特征根迹检验中，每一行的迹统计量都大于临界值，也即不存在协整向量、最多有1个特征向量和最多2个特征向量的原假设在5%的显着性水平上都被拒绝了。同样在最大特征根检验中，每一行的最大特征根统计量都大于临界值，三行中的原假设在5%显着水平上也都被拒绝了。这两种检验方法都接受了至少存在3个协整向量的备择假设，表明LR、LNM、LNG这三个时间序列之间存在着协整关系。表3-5给出了Johansen协整检验所输出的标准化协整系数。

　　3.1.2.4 模型建立

　　本文选取DLR、DLNM、DLNG这三个平稳的差分时间序列构建VAR模型，这需要确定最优的滞后阶数。表3-6给出了用DLR、DLNM、DLNG三个时间序列数据构建VAR模型时，不同判断准则下最优滞后阶数的选择结果。

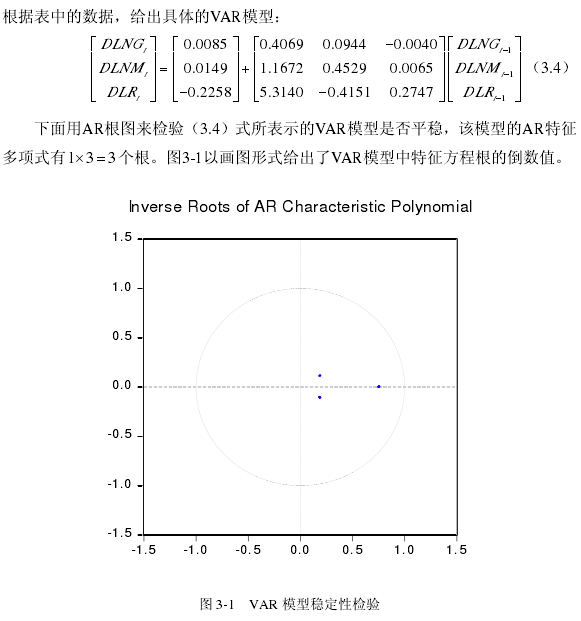
　　从图中可以看出所有根的倒数的模均小于1,位于单位圆之内。因此，可以确定由DLR、DLNM、DLNG这三个时间序列构建的一阶滞后VAR模型是稳定的。

　　3.1.2.5 Granger因果检验

　　判断一个变量的变化是否是另一个变量变化的原因，是分析经济变量相关性的常见问题，本小节用Granger因果检验来判断DLR、DLNM、DLNG这三个经济变量之间是否存在因果关系。Granger因果检验的思想：如果Y 影响 X ,或者Y 是 X 的原因，此时Y 的变化必然先于 X 的变化，即根据Y 的过去值对 X 进行回归时，如果加上 X 的过去值，能显着增强回归的解释能力。表3-8给出了对DLR、DLNM、DLNG这三个变量进行Granger因果检验的结果。

　　从表中的检验结果可知：

　　（1）当DLNM作为被解释变量时，DLNG的2值为10.96908,在1%显着水平下拒绝了DLNG不是DLNM格兰杰原因的原假设，即序列DLNG是序列DLNM统计意义上的的格兰杰原因；（2）当DLR作为被解释变量时，DLNG的2值为4.077256,在5%显着水平下拒绝了DLNG非DLR格兰杰原因的原假设，即DLNG在格兰杰意义下也影响DLR的变动。（3）当DLNG作为被解释变量时，DLNM的2值为5.174691,在5%显着水平下也拒绝了原假设，即DLNM在格兰杰意义下可以解释DLNG的变动，但DLR对DLNG的格兰杰影响不显着。

　　综上所述，在格兰杰意义下，GDP增长率的变化能够显着影响货币供应量的变动和贷款利率的变化；反之，货币供应量的变动率也能够解释GDP的变化，但贷款利率对GDP的影响不显着。因此，日本货币政策的变化与经济周期的波动是相互影响的，但周期的波动更显着地先行于货币政策的变化，日本货币政策的实施或者货币政策产生的作用，显着滞后于经济周期的波动，货币政策的有效性较低。

　　3.1.2.6 脉冲响应分析

　　用脉冲响应函数可以分析某内生变量的随机扰动项发生一个冲击时，对其他内生变量及整个系统的影响。

　　本小节通过绘制脉冲响应函数图，分别考察给予变量DLNG、DLNM、DLR一个新信息脉冲对另外两个变量产生的影响。脉冲响应函数图中，纵坐标表示变量对脉冲的响应程度，横坐标代表滞后期。

　　第一，DLNM、DLR对DLNG冲击的脉冲响应分析。

　　（1）图3-2给出了DLNM对DLNG冲击产生的脉冲响应。给DLNG施加一个正向的冲击后，会在当期给DLNM带来负向影响，但DLNM的响应很快转为正向，响应程度在在第2期达到最高点0.030149.之后响应程度逐渐下降，随着滞后阶数的增加，DLNM的响应趋向于0.

　　（2）图3-3给出了DLR对DLNG冲击产生的脉冲响应。DLR在当期迅速做出了负向响应，并很快转为正向响应，其响应程度也在第2期达到最高点0.130173.之后DLR的响应与DLNM的响应一样逐渐下降，并趋向于0.

　　DLNM、DLR对DLNG冲击的脉冲响应结果说明，GDP的变动对货币供应量和贷款利率带来了较为相同的影响，GDP的正向变动会立即引起货币政策反方向的变化，但由于政策时滞的影响，政策产生的效应变为正向。也就是说，货币政策在很大程度上加强了经济周期的波动幅度。

　　第二，DLNG对DLNM和DLR冲击的脉冲响应分析。

　　（1）图3-4给出了DLNG对DLNM冲击产生的脉冲响应。在当期给DLNM施加一个正向冲击后，DLNG没有立即做出响应，但之后响应程度剧烈上升，并在第2期达到正向最高点0.008009.之后DLNG的响应缓慢下降，随着滞后阶数的增加，响应程度趋向于0.

　　（2）图3-5给出了DLNG对DLR冲击产生的脉冲响应。在当期给DLR施加一个正向冲击后，DLNG同样没有变动，之后出现了负向响应，其程度在第2期达到负向最高点-0.002434.之后DLNG的响应程度逐渐趋向于0.

　　DLNG对DLNM和DLR冲击的脉冲响应结果说明，日本的货币政策在当期实施后，其效力的产生存在一年的时滞，在第2期对GDP的变动产生影响。