运用时间序列的建模方法对CPI指数序列拟合预测

　　一、引言

　　CPI 指数，即消费者物价指数（Consumer Price Index），英文缩写为 CPI,是反映与居民生活有关的产品及劳务价格统计出来的物价变动指标，是用来判断是否出现通货膨胀的重要衡量标准，如果 CPI 指数上升较为缓慢温和，则说明经济增长稳定，没有通货膨胀或通货膨胀轻微。

　　受全球金融危机的影响，2008 年 8 月份开始，我国 CPI 指数一路下滑，自 2009 年 4 月份开始更是出现了连续 3 个月的同比负增长。短短 1 年时间，CPI 指数从 2008 年 4 月份的同比上涨 8. 5%变为 2009 年 4 月份同比下降 1. 5%.ARMA模型，即自回归移动平均（auto regression movingaverage）模型，许多学者将其运用于经济、旅游、能源、医学、环境等众多领域并获得了较好的成果.

　　本文选择1990年1月至2013年11月共 287 个月的中国 CPI 指数为研究对象，应用乘积模型进行分析，运用时间序列的建模方法对该 CPI 指数序列进行拟合、预测分析，主要目的是给居民的消费行为和政府的政策决策提供支撑。

　　二、基于 SAS、Eviews 软件的实证分析

　　（一）绘制序列时序图

　　我们用相关统计分析软件绘制序列时序图，时序图显示该序列前面一段时间有明显的一个峰谷，显然不平稳.

　　（二）差分平稳化

　　对原序列作1阶12步差分，希望提取原序列趋势效应和季节效应，得到差分后序列时序图，该时序图显示差分后序列类似平稳.

　　（三）模型定阶

　　为进一步进行平稳性判断，在此考察差分后序列自相关图的性质，并估计拟合模型的阶数。

　　自相关图显示延迟12步自相关图系数显着大于2倍标准范围，这说明差分后序列中仍蕴含着非常显着的季节效应。延迟 1 步、2步的自相关系数也大于2倍标准差，这说明差分后序列还具有短期相关性.

　　同样，观察偏自相关图得到的结论和上面的结论一致.我们可以用单位根检验进一步对差分后的数据进行检验其平稳性。Tau 统计量的 P 值显着小于 0. 05,可以认为序列显着平稳。我们用 SAS 在 identify 后面添加 minic 选项，根据 BIC 信息量最小原则，得出ARMA（2, 0）模型最优，即AR（2），所以尝试拟合ARMA模型，拟合效果不理想，拟合残差通不过白噪声检验。说明简单的 ARMA 模型并不适合于拟合这个序列。考虑到该序列既具有短期相关性又具有季节效应，短期相关性不能简单、可加性地提取，因而估计该序列的季节效应和短期相关性之间具有复杂的关联性。这时，通常假定短期相关性和季节效应之间具有乘积关系，尝试使用乘积模型来拟合序列的发展.

　　乘积模型的构造原理如下：

　　当序列具有短期相关性时，通常可以使用低阶 ARMA（p, q）模型提取；当序列具有季节效应，季节效应本身还具有相关性时，季节相关性可以使用以周期步长 S 为单位的 ARMA（P, Q）模型提取。

　　由于短期相关性和季节效应之间具有乘积关系，所以拟合模型实质为假设短期相关和季节效应之间具有乘积关系，模型结构如下ARMA（p, q）和 ARMA（P, Q）的乘积。综合前面的 d 阶趋势差分和D 阶以周期 S 为步长的季节差分运算，对原观察值序列拟合的乘积模型完整的结构如下：

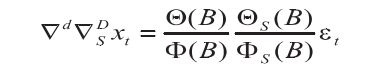
　　该乘积模型简记为 ARMA（p,d,q）×ARMA（P,D,Q）s.回到模型的定阶阶段，考虑到差分后序列短期相关性显着，尝试拟合乘积模型 ARMA（1,1,1）×ARMA（0,1,1）12.

　　（四）参数估计使用条件最小二乘法估计方法得到参数估计值，如图：

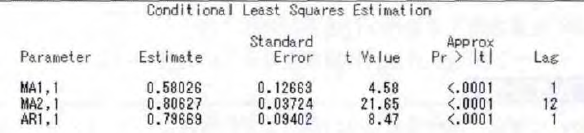
　　（五）模型检验对拟合模型进行检验，上图显示该模型通过参数显着性检验（因为 P 值显着小于 0. 05），同时，模型也通过了残差白噪声检验。

　　（六）最终模型由 SAS 结果可知拟合模型的口径为：

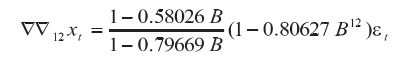
　　将序列拟合值和序列观察值联合作图，可以直观地看出该乘积模型对原序列的拟合效果良好。

　　三、模型的预测

　　为了验证模型预测的准确程度，我们现对2013年9月到11月年过去的三个月进行预测，并用真实值与预测值进行比较，结果如下所示：2013年9月预测值为102. 8470%,实际值为103. 1%;2013 年 10 月预测值为 103. 2154%,实际值为 103. 2%;2013 年 11 月预测值为 103. 5808%,实际值为 103. 0%.由结果可知，模型的预测效果是良好的。

　　利用此模型对 2013 年 12 月、2014 年 1~4 月份的全国 CPI 指标进行预测，预测结果如下：2013年 12 月的 CPI 为 103. 7530%;2014 年 1 月的 CPI 为103. 8944%;2014 年 2 月 的 CPI 为 104. 0915%;2014 年 3 月 的 CPI 为104. 3359%;2014 年 4 月的 CPI 为 104. 6792.

　　四、结论及建议

　　通过采用本文选择1990年1月至2013年11月共287个月的中国 CPI 指数的月度数据建立结构模型，实证考察了我国 CPI 波动，得到了以下结论。

　　一方面， 由模型预测值可看出，在未来的一段时间内 CPI 将会持续保持在102左右，环比增长率将保持在2%以上，数据基本符合市场预期，物价总体回落趋势已形成。究其原因，可能是由于国内总需求增长速度下降，对 CPI 的推动作用减弱。因受全球经济下滑的影响，我国进出口总额也将出现一定程度下滑，影响CPI的波动.

　　另一方面，由预测结果可知，我国今年出现通货膨胀的可能性不大，中国CPI之所以出现走低状况，可能是由于宏观调控的力度过渡所致，政府应给予相应的适度刺激政策，并全面准确地跟踪监测价格运行情况，及时把握和应对可能出现的价格新情况；同时，调整国民收入分配政策，使收入分配适当向居民倾斜，健全社会保障体系，增加居民消费信心，促进消费需求增长；最后，及时有效地落实房地产调控政策，稳定居住价格.

　　参考文献

    [1]何晓群。多元统计分析[M].北京：中国人民大学出版社，2012.
　　[2]王燕。应用时间序列分析（第二版）[M].北京：中国人民大学出版社，2008.基金项目：基于 ARMA 乘积模型的 CPI 指数分析及预测。