基于COVID-19传播机制的SEIR数学模型构建应用

　　摘    要：　目的 针对新型冠状病毒肺炎(coronavirus disease 2019,COVID-19)感染进行数学建模,预测疫情的发展趋势,并为该病的防控提供参考。方法 采用SEIR模型进行数学建模,收集自2020年01月10日至2020年02月28日中国国家卫健委公布的当前感染人数、治愈人数和死亡人数的数据,对模型进行参数估计;并针对模型中不同参数的变化,预测疾病未来发展趋势。结果 根据COVID-19传播机制,建立了SEIR模型,并基于国家卫健委公布的数据,通过fmincon和lsqnonlin函数对建立的数学模型进行分阶段拟合,感染人数和移出人数的相关性分别为99.9%和99.8%,预测的误差率分别为0.67%和0.89%。结论 基于中国近一个月来COVID-19发病率数据,本研究建立了精准度较高的数学模型,通过数学模型的精确分析和有效预测,结果提示对潜伏期人群和感染人群进行严格隔离,同时不断提高患者的移出率,可有效控制该传染病疫情。

　　关键词：　新型冠状病毒肺炎; 数学建模; 参数估计; 预测; 控制策略;

　　Abstract：　Objective The aim of this study was to propose a mathematical modeling for the coronavirus disease 2019(COVID-19) epidemic to predict the development trend of the epidemic, which will provide guidance to the epidemic prevention and control. Methods The mathematical modeling was performed using the SEIR model, and the data of the current number of infections, cures, and deaths issued by the National Health Commission of China(NHCC)from January 10, 2020 to February 28, 2020 were collected. Parameters of the model were estimated, and the trend of the epidemic was forecasted in terms of different parameters. Results Based on transmission mechanism of the COVID-19, a SEIR model was proposed. According to data published by NHCC, the parameters of mathematical model were estimated in different stages by fmincon and lsqnonlin functions. The correlations of the infected people and the removed were 99.9% and 99.8%, respectively. The prediction error rates were 0.67% and 0.89%, respectively. Conclusions Based on the data of COVID-19 in China issued by NHCC, this study established a mathematical model with effective prediction. The results suggest that the exposed and the infected population should be strictly isolated. At the same time, with continuously improving the removal rate of patients, the epidemic will be effectively under control and terminated.

　　自2019年12月武汉报道不明原因的肺炎病例以来截至到2020年2月28日,中国累计感染病例79 251人。造成本次新型冠状病毒肺炎(coronavirus disease 2019,COVID-19)的病毒命名为新型冠状病毒(severe acute respiratory syndrome coronavirus 2, SARS-CoV-2),其传染源为新型冠状病毒感染的患者,而无症状的感染者也可能成为传染源。新型冠状病毒传播途径主要是呼吸道飞沫和接触传播。人群普遍是新型冠状病毒的易感人群,且老年人及有基础疾病者感染后病情较重。流行病学研究这类急性传染病的一种重要的方法是数学建模。

　　自从本次疫情暴发,已有研究相继对COVID-19进行了数学建模和预测分析[1,2,3,4,5,6,7,8,9]。其中Wu等[4]基于建立的SEIR模型,预测了COVID-19的基本再生数为2.68,并预测截至2020年1月25日,武汉感染人数将为75 815。同时,研究者也预测了从武汉输入到重庆、北京、上海、广州和深圳的感染者的数量。但是,该研究报道的预测数据与目前国家卫健委发布的武汉感染人数不太一致,相差数量较大。本研究基于COVID-19传播机制重新建立SEIR数学模型,并结合国家卫健委发布的全国感染的人数,对模型参数进行估计,旨在得到更为精确的数学模型,为控制COVID-19疫情提供参考依据。
 

　　1、 资料与方法

　　1.1、 研究方法

　　研究传染病最经典的模型为SIR仓室模型,该模型由Kermack和McKendrick在1927年研究黑死病时提出[10]。SIR模型把人群分成三类:易感者(Susceptible),指缺乏免疫能力的未感染者;感染者(Infective),指患病的人,具有传染性,可感染易感者;移出者(Removed),指死亡或者治愈者。其基本模型为:

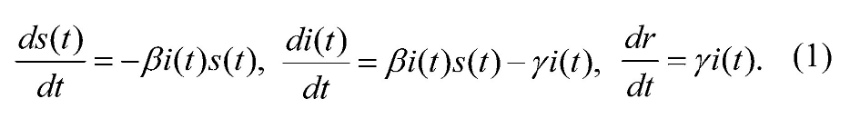
　　模型(1)中s(t),i(t)和r(t)分别是易感人群,感染人群和移出人群,β是感染率,γ是恢复率。

　　随着研究的深入,研究者逐渐认识到一些传染病感染人群后,出现症状需要一定的时间,并将这段时间称之为潜伏期。因此,有人提出以下SEIR模型:

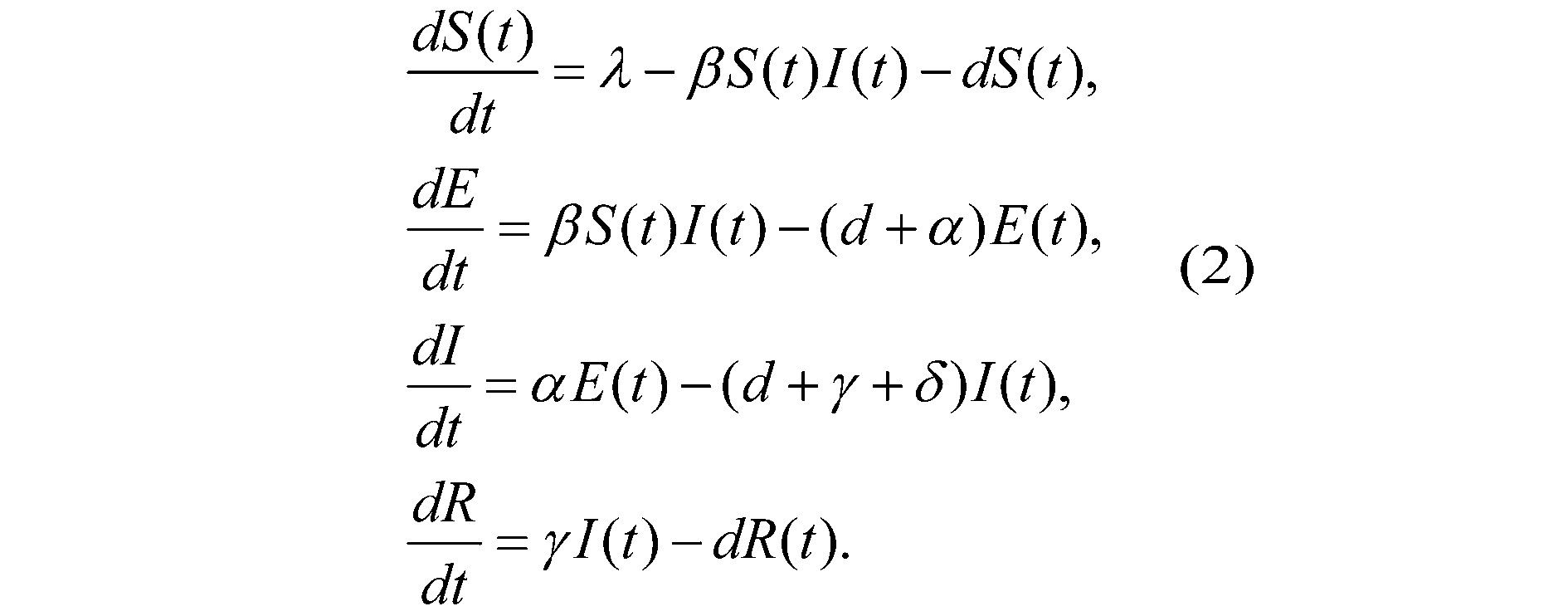
　　基于上述模型,本研究将人群分成易感者(S),暴露者(E),感染者(I)和恢复者(R)四类人群。根据经典SEIR传染病传播机制,本文采用了如图1所示的传播模式。

　　图1 SEIR传染病传播机制

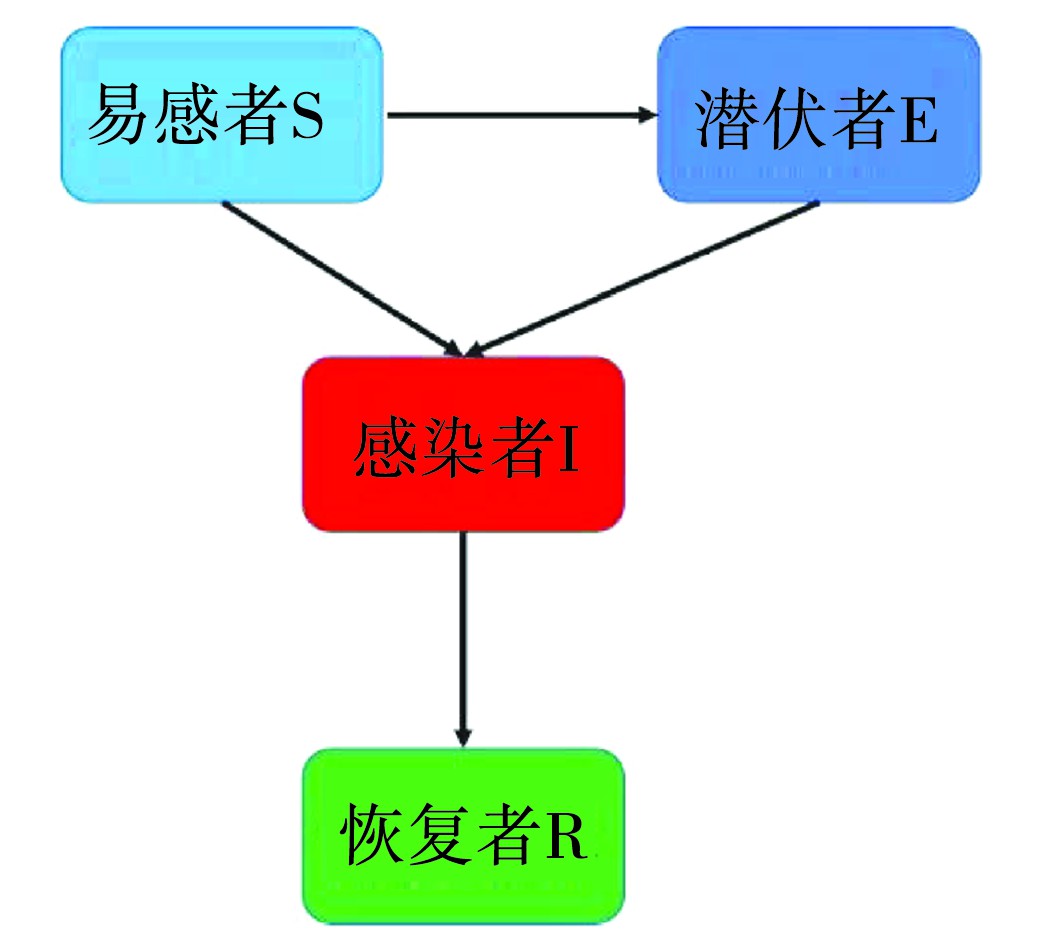
　　Figure 1 The transmission mechanism of SEIR infectious disease

　　在本次疫情中,在短期时间内,忽略了新生儿和全体人群的自然死亡率。鉴于该疾病在潜伏期亦有传染性,本研究建立如下数学模型:

　　公式(3)中S(t)表示易感人群,E(t)表示潜伏期人群,I(t)表示当前感染人群,R(t)表示移出患者人群。r表示感染者平均每天接触易感者的人数,β表示感染者感染易感人群的概率,r2表示潜伏者平均每天接触易感者的人数,β2表示潜伏者感染易感人群的概率,δ潜伏者转化为感染者概率,γ表示移出率,N(t)是全部人群的总和。

　　表1 调查对象基本情况

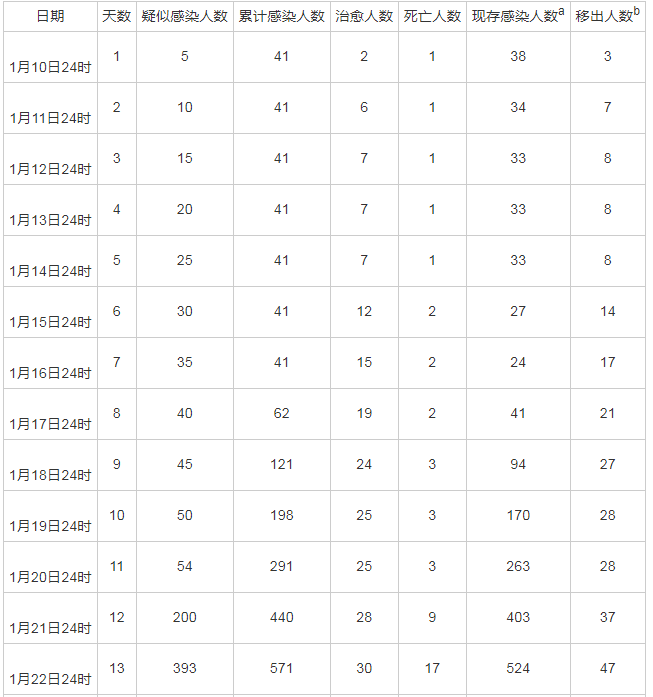
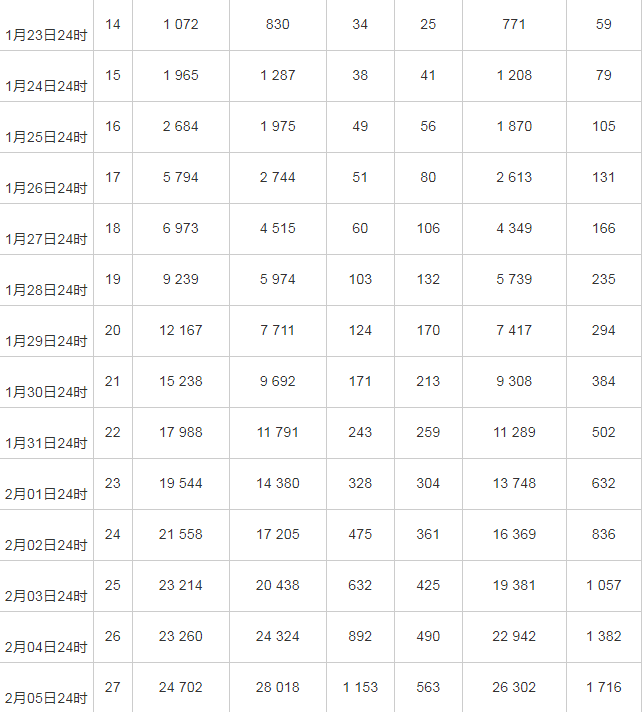
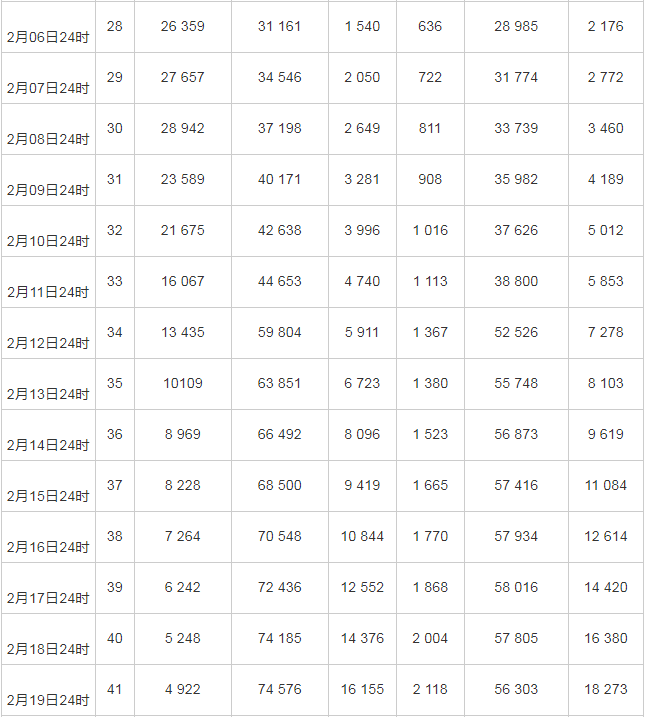
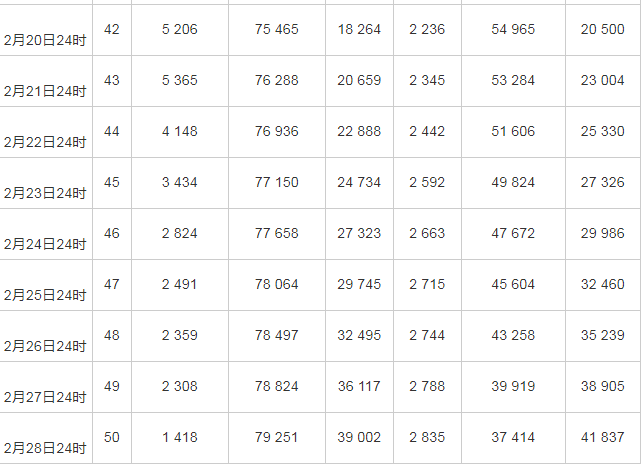
　　注:a现存感染人数=累计感染人数-治愈人数-死亡人数; b移出人数=治愈人数+死亡人数。

　　接下来,本研究将根据国家卫健委发布的每日24时当前感染人数,治愈人数和死亡人数的数据对模型进行参数估计,得到精准度较高的数学模型。基于国家卫健委公布的数据,统计结果见表1。

　　基于上述数据,采用matlab 2017b的fmincon和lsqnonlin函数对参数进行估计。因为国家采取了多种措施进行防治,因此本研究采用多阶段拟合。

　　2、 结果

　　2.1、 模型参数估计和预测

　　基于表1,采用数据驱动建模,因为本次疫情发展中,国家采取了一系列的措施,比如建立火神山医院、雷神山医院、方舱医院、武汉封城、居家隔离、派遣医疗队等,本研究共分为六个阶段,对模型的参数进行拟合,具体如下:

　　第一阶段:本次疫情从1月10日到1月22日,没有采取任何隔离措施,初始人数为:全国人数1.4×109,易感者为(1.4×109-41-2)人,潜伏者0人,感染者41人,治愈者2人。感染者每天接触人数为r=20,传染概率为β=0.043,即βr=0.86,与文献[7]预测的0.8接近。潜伏者每天接触人数为r2=20。因为潜伏期传染概率低于确诊患者的传染概率,故设为β2=0.025。潜伏者转化为确诊患者的概率为δ=0.079[11],移出率为γ=0.001[12]。

　　第二阶段:1月23日,开始采取针对性隔离措施。但是因为床位和隔离力度有限,此时确诊感染者每天平均接触人数为r=2,潜伏者平均每天接触人数为r2=7。同时,国家派了大量医疗队,移出率得到提高,为γ=0.006 5。此时的调控定义为干预措施1。

　　第三阶段:自2月5号开始,随着进一步加强确诊率并及时进行小区、社区、农村街道的防控管理,感染者每天的平均接触人数下降到r=0.1,潜伏者接触人数为r2=2,移出率达到γ=0.02。此时的调控为干预措施2。

　　第四阶段:自2月12号开始,国家将临床诊断方法用于COVID-19的确诊,因此调整当前确诊人数为52 526,确诊感染者每天的平均接触人数下降到r=0.01,潜伏者接触人数为r2=2,移出率为γ=0.023。潜伏者转化为确诊患者的概率为δ=0.12。

　　第五阶段:从2月18日开始,随着进一步筛查以及派遣更多的医疗队支援武汉,参数如下:r=0.01;β=0.004 3;r2=0.5;β2=0.002 5;γ=0.04;δ=0.04。

　　第六阶段:从2月23日开始,参数如下:r=0.01;β=0.004 3;r2=0.5;β2=0.002 5;γ=0.04;δ=0.04。

　　基于上述六个阶段,得到的临床统计数据和数学模型结果,见表1、图2。本文采用2020年01月10日作为起始点,2020年02月15日24时的数据作为训练集,进行模型参数估计,感染人群和移出人群拟合的相关性分别为99.9%和99.8%。以2020年2月16日24时到28日24时数据作为验证,结果见表2。经计算,感染人群的平均预测误差为0.67%,移出人群的平均预测误差为0.89%。

　　2.2、 参数对疫情的影响

　　2.2.1、改变移出率对疫情的影响(γ)

　　第51天开始(2020年2月29日),其余参数保持不变,改变移出率γ(γ=0.03,0.05,0.07,0.09),对感染人群和移出人群的影响,探索对本次COVID-19疫情的影响。 图3中的绿色线是国家2020年1月23号开始进行隔离和治疗,称为干预措施1,其中的黑色线是2020年02月05开始进一步加强隔离和投入更多医疗资源,称为干预措施2。实线表示当前的移出率。从图3看到,当移出率γ=0.03时,COVID-19患者会持续200天以后才会消失,随着移出率由0.03增加到0.09,感染人数消失的时间也会相应的缩短。例如,当移出率γ=0.03时,感染人数到第200天还存在,当移出率γ=0.09时,第125天时感染的人数已经消失,因此提示:如果能提高患者的移出率,本次疫情得到有效的控制的时间将提前至少75 d。图4是在不同移出率条件下,移出者人数变化趋势。移出率越高,SEIR系统达到稳定的时间越短,这也和图3感染人数消失的时间越早是相对应的。

　　2.2.2、 感染者的隔离率对疫情影响(r)

　　本节研究感染者的隔离率(r)对疫情影响,实线(r=0.01)表示当前对感染者的隔离率。当感染者平均每天接触人数为r=0.01时,疫情能够得到很好的控制,最后感染的人群将会消失,但是如果确诊患者平均每天接触人群从0.01逐渐增加到4时,感染的人数将持续大量存在,疫情得到控制将在200 d之后(见图5)。因此,积极响应国家号召,及时做好患病人群的隔离,国家各地区的“汤山医院”的建立,是非常有效的措施。

　　2.2.3、 潜伏者的隔离率对疫情的影响(r2)

　　接下来通过数值仿真的方法研究潜伏者的隔离率(r2)对疫情的影响。实线(r2=0.01)表示当前对潜伏者的隔离率。当潜伏者平均每天接触人数r2=0.1时,感染者人数变化趋势如图6的实线所示。如果潜伏者平均每天接触人数从0.1逐渐增加至5,疫情的将变得无法控制。例如,当潜伏者平均每天接触人数r2=0.1时,第150天时感染的人数将消失,而当潜伏者平均每天接触人数r2=5时,感染的人数将先减少后逐渐增加,疫情将会再次暴发。

　　图2 易感人群、潜伏期人群、感染人群和移出人群的动力变化趋势

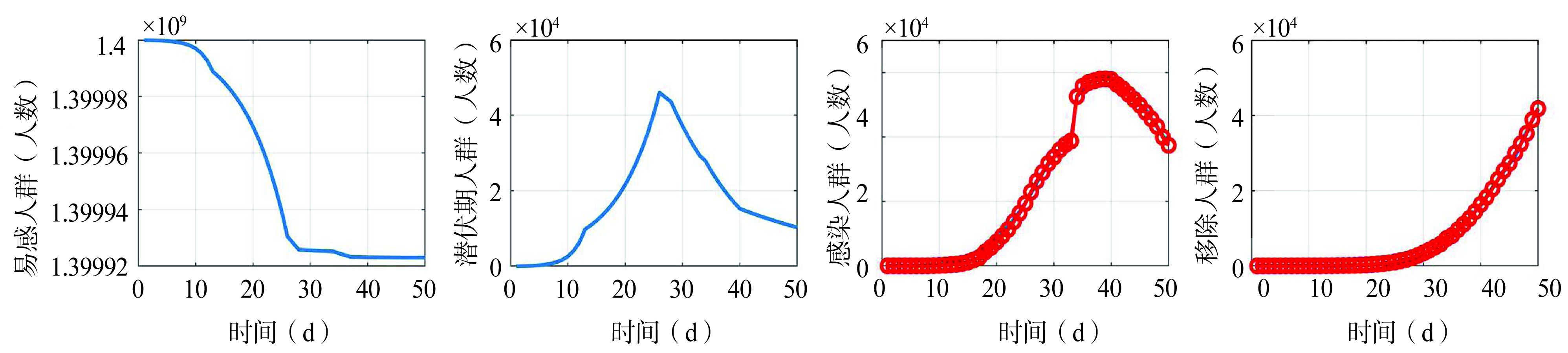
　　Figure 2 The dyamic trends of susceptible, exposed, infected and removed

　　表2 预测2月16到28日的感染人数和移出人数

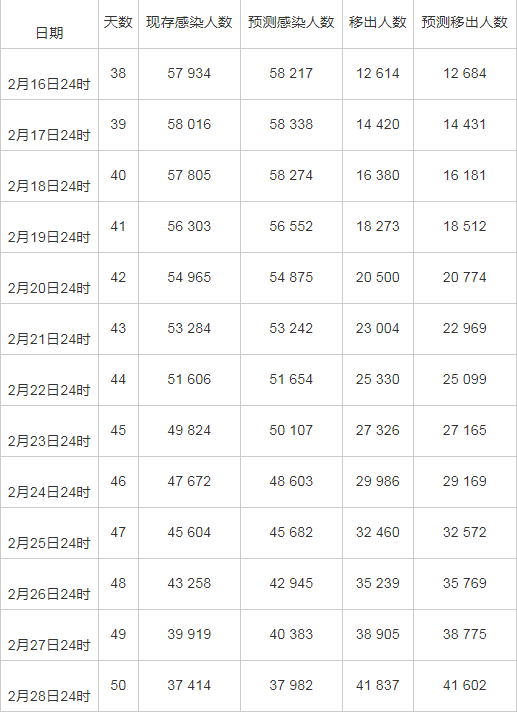
　　图3 当移出率γ从0.03逐渐增加到0.09时感染者人数变化趋势

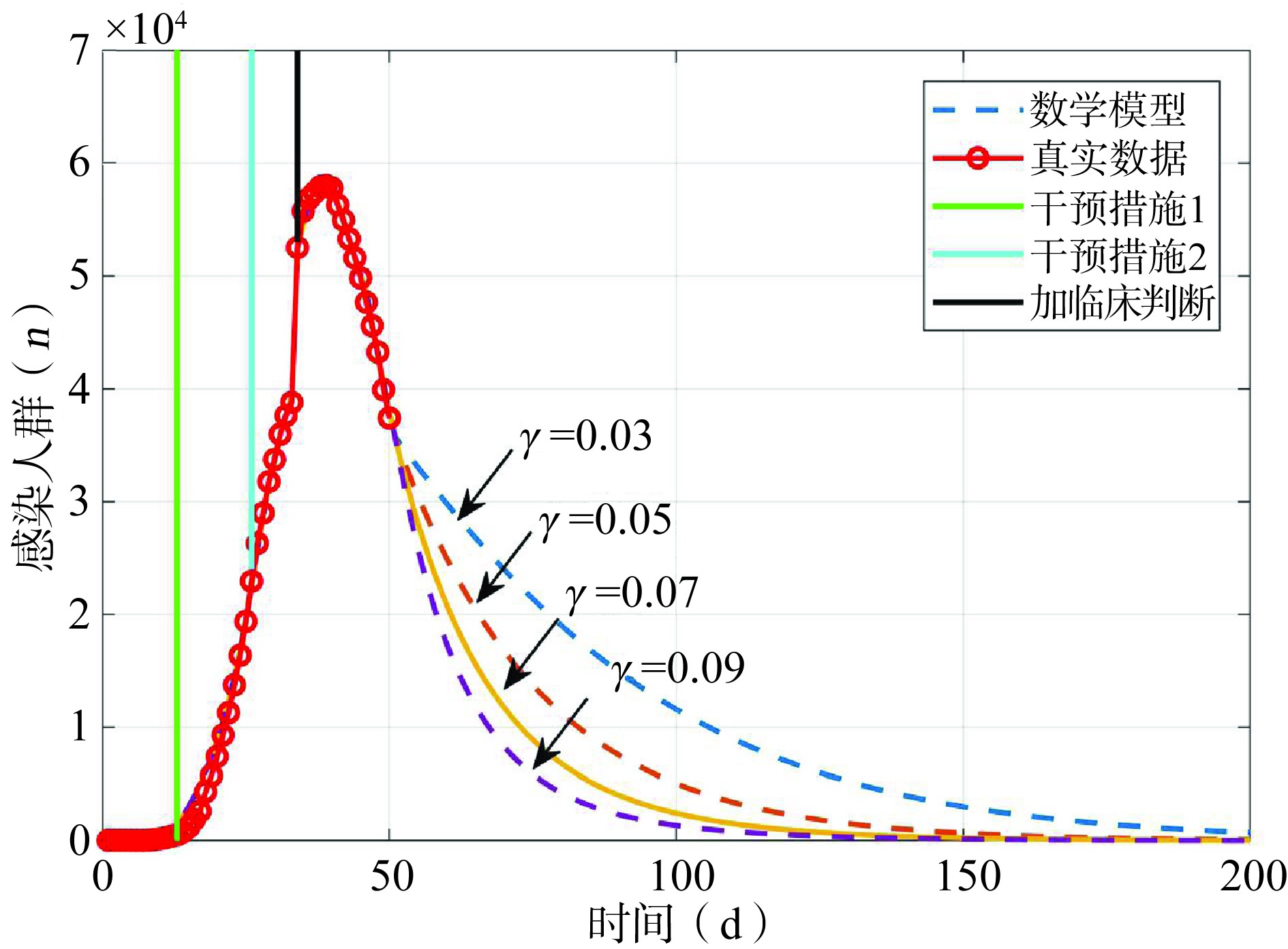
　　Figure 3 The dynamic trend of the infected when removal rate (γ) increased from 0.03 to 0.09

　　图 5 当确诊患者的接触率r从0.01逐渐增加到4时感染者人数变化趋势

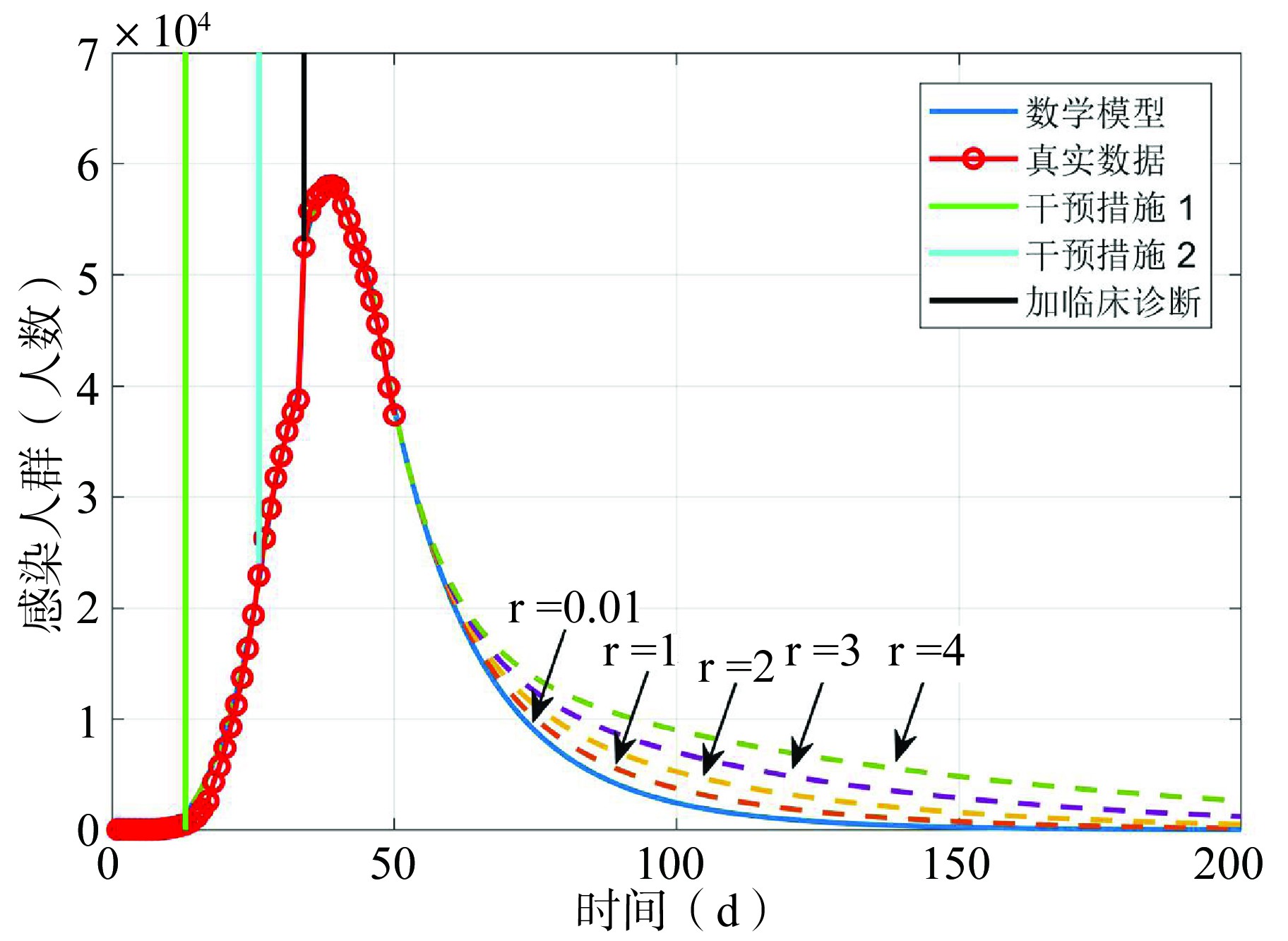
　　Figure 5 The dynamic trend of the infected when contact rate of the infected (r) increased from 0.01 to 4

　　图 4 当移出率γ从0.03逐渐增加到0.09时移出人数变化趋势

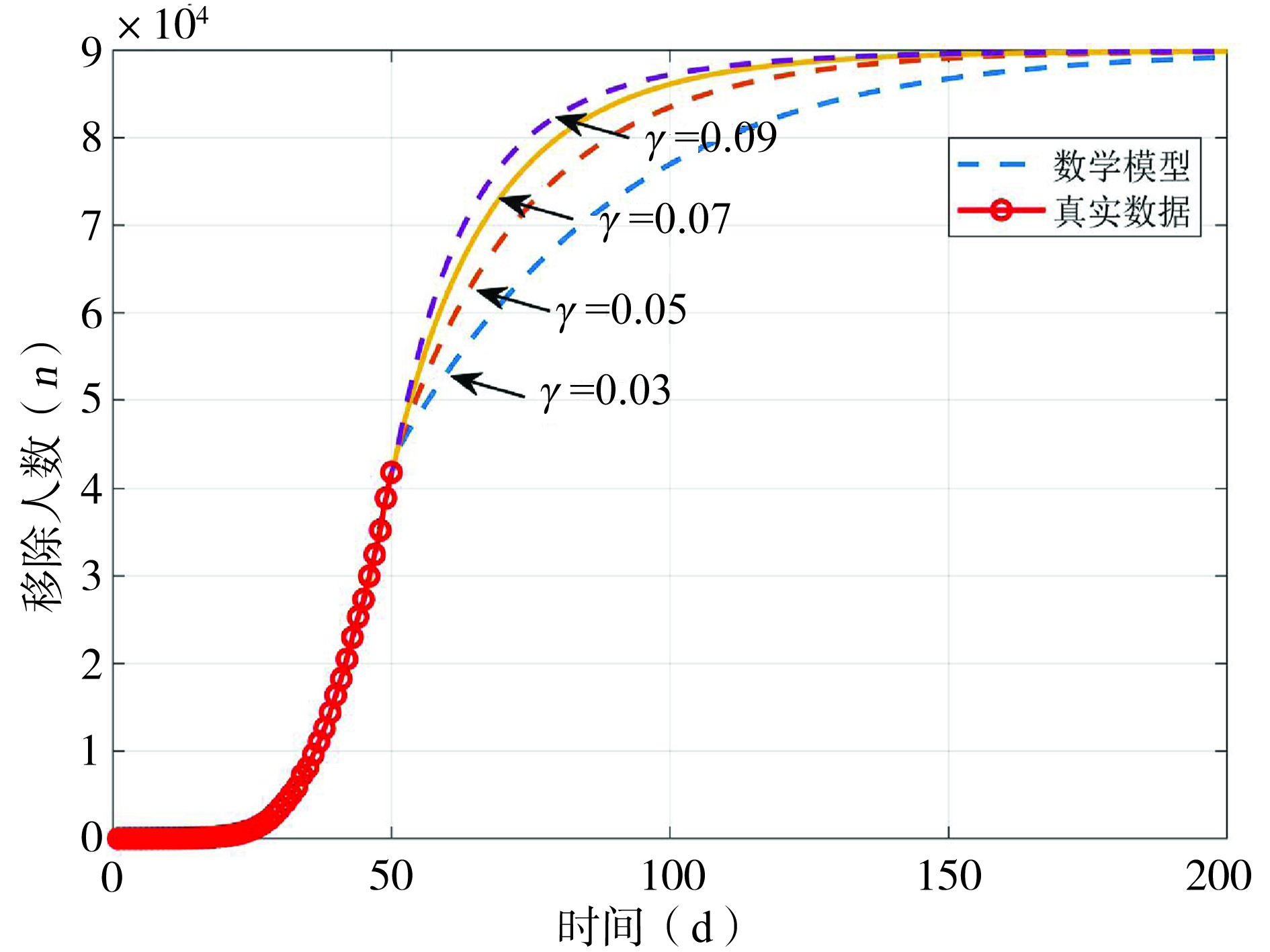
　　Figure 4 The dynamic trend of the removed when removal rate (γ) increased from 0.03 to 0.09.

　　图 6 当潜伏者的接触率r2从0.1增加到5时感染者人数变化趋势

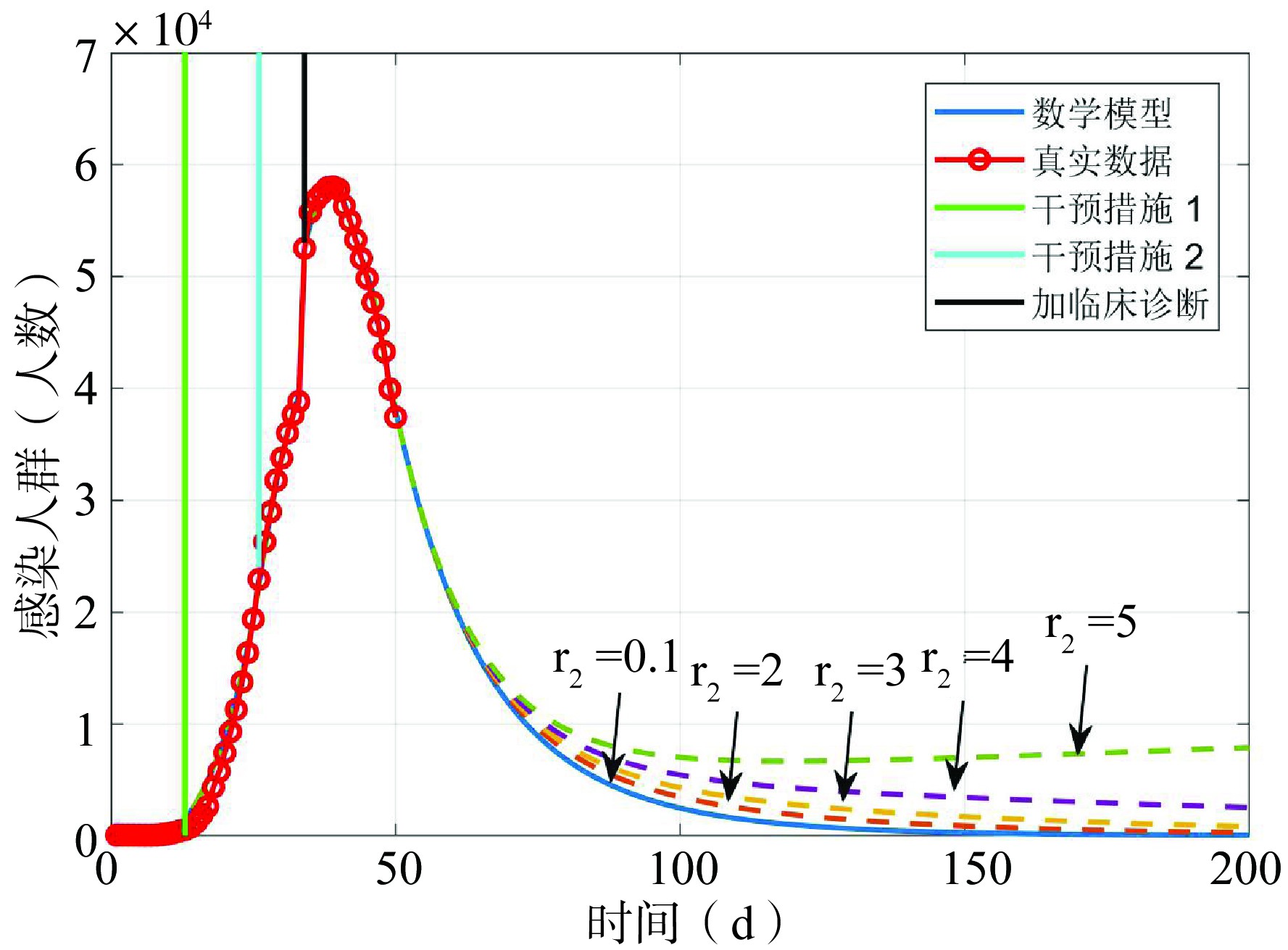
　　Figure 6 The dynamic trend of the infected when contact rate of the exposed (r) increased from 0.1 to 5

　　3、 讨论

　　针对突发的急性传染病疫情,通过建立精确的数学模型,科学预测疾病的发展趋势和传播动态,可为疾病的有效防控提供理论指导。

　　本研究通过SARS-CoV-2的传播机制采用了经典的SEIR模型进行数学建模。基于国家卫健委发布的数据,对模型参数进行估计,并预测了短期内感染人群和移出人群的变化趋势,平均误差率分别为0.67%和0.89%。相较于Natsuko等[13]预测的截至2020年1月18日,将有4 000例感染,而国家卫健委公布的当前感染人数为94人;Gardner等[14]预测,截至2020年1月25日,将有20 000人感染,国家卫健委公布的当前感染人数是1 870人;Ai[7]建立的SEIR模型预测湖北疫情达到峰值的时间是2020年1月28到2月7日之间,并且感染的人数为7 000～9 000,而本次疫情达到峰值的时间是2月18日;本研究所建立的数学模型的主要优势是采用国家卫健委公布的数据进行多阶段分布拟合和参数估计,具有更高的预测准确率,感染人数和移出人数的相关性分别为99.9%和99.8%,预测的误差率分别为0.67%和0.89%。接下来研究了移出率γ,确诊患者的接触率r和潜伏者的接触率r2对本次COVID-19疫情的影响,本研究结果对我国武汉等地区新型冠状病毒肺炎防治工作具有重要的指导意义。

　　本研究基于COVID-19传播机制重新建立SEIR数学模型,结合国家卫健委发布的全国感染人数,对模型参数进行估计,得到了精确的数学模型。通过数学模型的精确分析和有效预测,提示对潜伏期人群和感染人群进行严格隔离,同时不断提高患者的移出率,可有效防控疫情。

　　参考文献

　　[1] Tang B,Wang X,Li Q,et al.Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions [J].J Clin Med,2020,9(2):462-474.DOI:10.2139/ssrn.3525558.
　　[2] Gabriel L,Joseph W.Real-time nowcast and forecast on the extent of the Wuhan CoV outbreak,domestic and international spread[EB/OL].(2020-01-27) [2020-02-12].https://www.med.hku.hk/f/news/3549/7418/Wuhan-coronavirus-outbreak_AN-UPDATE_20200127.pdf.
　　[3] Read JM,Bridgen JR,Cummings DA,et al.Novel coronavirus 2019-nCoV:early estimation of epidemiological parameters and epidemic predictions [J].medRxiv,2020.01.23.20018549.DOI:10.1101/2020.01.23.20018549.
　　[4] Wu JT,Leung K,Leung GM.Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan,China:a modelling study [J].Lancet,2020,395(10225):689-697.DOI:10.1016/S0140-6736(20)30260-9.
　　[5] Chen TM,Rui J,Wang QP,et al.A mathematical model for simulating the transmission of Wuhan novel Coronavirus [J].bioRxiv,2020.01.19.911669.DOI:10.1101/2020.01.19.911669.
　　[6] Chen Y,Cheng J,Jiang Y,et al.A time delay dynamical model for outbreak of 2019-nCoV and the parameter identification [J].arXiv,2002.00418v1.2020.
　　[7] Ai LZ.Modelling the epidemic trend of the 2019-nCOV outbreak in Hubei Province,China [J].medRxiv,2020.01.30.20019828.DOI:https:10.1101/2020.01.30.20019828.
　　[8] Zhou T,Liu QH,Yang ZM,et al.Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV [J].arXiv,2001.10530.
　　[9] Liu T,Hu JX,Kang M,et al.Transmission dynamics of 2019 novel coronavirus (2019-nCoV) [J].bioRxiv,2020.01.25.DOI:10.1101/2020.01.25.919787(preprint).
　　[10] 马知恩.传染病动力学的数学建模与研究 [M].北京科学出版社,2004.Ma ZE.Mathematical modeling and research of infectious disease dynamics [M].Beijing Science Press,2004.
　　[11] Chowell G,Castillo-Chavez C,Fenimore PW,et al.Model parameters and outbreak control for SARS [J].Emerg Infect Dis,2004,10(7):1258-1263.DOI:10.3201/eid1007.030647.
　　[12] Zhang C,Wang M.Origin time and epidemic dynamics of the 2019 novel coronavirus [J].bioRxiv,2020.01.25.919688.DOI:10.1101/2020.01.25.919688.
　　[13] Natsuko I,Ilaria D,Anne C,et.al.Estimating the potential total number of novel Coronavirus cases in Wuhan City,China [EB/OL].(2020-01-17) [2020-02-12].https://www.preventionweb.net/go/70092.
　　[14] Gardner L,Zlojutro A,Rey D,et.al.Modeling the spread of 2019-nCoV [EB/OL].(2020-01-26) [2020-02-12].https://systems.jhu.edu/wp-content/uploads/2020/01/Gardner-JHU_nCoV-Modeling-Report_Jan-26.pdf.