最优化方法在数学建模中的应用

　　摘    要：　计算和建模正在成为数学科学深入发展的强大驱动力，数学建模的思想和方法也被创造性地应用于各行各业和各科学领域。文章介绍了数学建模的含义、基本方法和一般过程，并介绍了最优化方法的相关理论，以及最优化方法在数学建模中的具体应用。

　　关键词 :     数学建模:最优化方法,数学应用;

　　1 、数学建模

　　1.1 、数学建模的含义

　　数学建模（Mathematical Modeling）是近几十年来出现的新词汇，但是运用数学方法解决那些数量规律的实际问题，却是始终伴随着人类社会的产生和发展的[1]。运用数学方法解决实际问题的首要一步是建立研究对象的数学模型，再借助计算机加以计算求解。数学模型，是对于现实世界的一个特定对象，为了一个特定目的，根据特有的内在规律，做出一些必要假设，运用数学符号、数学公式、程序、图形等对问题本质属性做出抽象而又准确的刻画，便于人们更深刻地认识所研究的对象[2]。

　　针对某一对象或问题建立数学模型，能够对客观规律进行量化的准确描述，或根据已有信息估测某特定参数的变化趋势，以便于做出合理决策。

　　1.2 、数学建模的方法与过程

　　数学建模，一般待解决的都是有着实际应用背景的问题，往往还需要相关的详细资料。建立数学模型的方法多种多样，常见方法包括机理分析方法、构造分析方法、直观分析方法、数值分析方法等[3]。

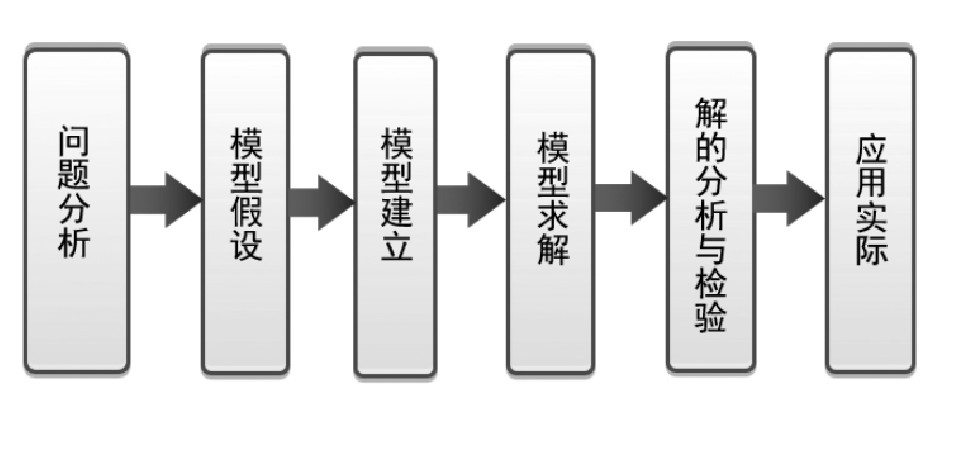
　　数学建模的一般过程如图1所示，其中，问题分析指的是分析待解决的实际问题和已知信息，明确要解决的问题是什么；模型假设指的是对问题进行合理的简化，抓住问题中的主要矛盾，合理地忽略次要矛盾，能够提高建模的效率和成功率；模型建立指的是综合运用数学方法建立实际问题的数学模型；模型求解指的是采用数学知识求解数学模型中的变量，对于较为复杂的模型，模型求解往往需要借助计算机来实现；求解模型后，还需要对求解的物理内涵和实际意义做出必要解释，并说明该模型的适用条件、分析解的误差，等等；最后，还要将所建立模型以及求解结果应用到实际问题中，进行检验和修正，建模工作才算基本完成。

　　图1 数学建模的一般过程

　　2 、最优化方法的概念

　　“优化”是生活中经常使用的词：坐出租车时希望司机不绕弯路、走优化路线；逛超市时考虑各种优惠活动，希望获得最大优惠；企业推出新产品要综合考虑成本与市场吸引力，对资金进行优化配置，等等。这些问题都是“最优化问题”，也是数学建模中的典型问题，解决最优化问题的数学方法就是“最优化方法”。最优化方法的出发点是系统思维，最优化方法的基本思路是在一定的约束条件下，保证各方面资源的合理分配，最大限度地提升系统某一性能或系统整体性能，最终实现最理想结果。

　　运用最优化方法建立并求解数学模型，主要包括以下步骤：

　　(1）明确目标，分析问题背景，确定约束条件，搜集全面的客观数据和信息；

　　(2）建立数学模型，构建变量之间的数学关系，设立目标函数；

　　(3）分析数学模型，综合选择最适合该模型的优化方法；

　　(4）求解模型，通常借助计算机和数学分析软件完成；

　　(5）对最优解进行检验和实施。

　　3 、最优化方法在数学建模中的应用

　　3.1 、梯度下降法

　　梯度下降法是经典的最优化方法之一[4]，其核心思想是高等数学中的导数理论。梯度下降法实现最优化的原理是，每次迭代更新目标函数时，都以该变量导数（即梯度）的反方向作为更新参数的方向，最终解一定会收敛于最优解。这个原理类似于走下坡路时，总是沿着最陡峭的方向向下走，最后就一定会走到坡底。

　　梯度下降法的实现简单，但是求解计算时间长，因此基于梯度下降法发展了很多改进算法，包括随机梯度下降法、小批量梯度下降法等，能够有效改善计算成本高的问题。

　　3.2、 惩罚函数法

　　惩罚函数法，指的是引入惩罚因子和惩罚函数的最优化方法[5]。具体来说，惩罚函数的思想是：将最优化问题中的约束条件视为围墙，而迭代更新的解视为在围墙内运动的粒子，一旦粒子靠近围墙，对应的惩罚因子数值就会增大，导致惩罚函数值增大，反之，粒子远离围墙时，惩罚函数值就减小。建立了这种惩罚机制后，在每次迭代过程中，模型为了“避免被惩罚”，逐渐趋近于约束边界，从而找到了最优解。

　　惩罚函数法对模型的训练虽然“简单粗暴”，但是原理直观、实现门槛低，是实际工程中备受青睐的最优化方法。

　　3.3 、遗传算法

　　不同于梯度下降法和惩罚函数法，遗传算法并非依据导数理论提出的算法[6]，而是一种模拟生物在自然届中进化规律的一种智能算法。自然界的生物进化遵循适者生存和优胜劣汰，即能够适应环境变化或基因变异的个体才能够参与到进化。遗传算法的优化原理与之类似：每一次迭代时，通过计算各个个体的适应度，从中随机地选择两个个体作为父母，繁殖后代，同时诱发子代的染色体变异，重复迭代，当出现最大适应度的子代时，即认为获得了最优解，循环结束。

　　与梯度下降法、惩罚函数法相比，遗传算法以生物进化为原型，收敛性较好，在计算精度要求时，具有计算时间少、鲁棒性高的优势。

　　3.4 、蚁群算法

　　与遗传算法类似，蚁群算法也是受启发于生物的一种最优化方法[7]。生物科学家发现蚂蚁经过的路上都会有一种特殊物质，并且蚁群中的蚂蚁对该物质高度敏感，由于该物质浓度越高，代表着路途长度越短，想要走“捷径”的蚁群们都会选择浓度较高的道路行走，“捷径”经过的蚂蚁越多，特殊物质的浓度就越高，物质浓度积累到一定程度，所有蚂蚁都会被吸引到最佳捷径上来，都能以最快速度找到食物了。蚁群算法解决最优化问题，就是利用了其分布计算和信息正反馈的特点。

　　蚁群算法适合解决参数多、纬度高等复杂问题，但同时容易陷入局部最优解，因此针对该方向的改进算法也是近年来的研究热点。

　　4 、结语

　　最优化问题是实际应用中常见的一类问题，关于最优化方法的讨论与研究也一直是相关领域的热点。为不同的数学模型选择合适的最优化方法，是数学建模领域最有价值的研究方向，不仅促进了数学方法的深入探究，也推动了科学和工程的进步。

　　参考文献

　　[1]赵天绪,阎思让高等数学下[M].北京:高等教育出版社, 2014.

　　[2]房少梅数学建模理论、方法及应用[M].北京:科学出版社，2014.

　　[3]崔建斌在高校理工科高等数学教学中渗透数学建模思想方法探索[J].德州学院学报, 2014(6):102- 105.

　　[4]杨涛,刘文杰，丁宁.基于梯度下降算法的神经网络模型研究[J]网络安全技术与应用。2013(4):75-77.

　　[5]李智勇.半定规划的微分代数算法和系列惩罚算法[D]福州:福建师范大学, 2006.

　　[6]包子阳，余继周基于MATL AB的遗传算法及其在稀布阵列天线中的应用[M].北京:电子工业出版社, 2017.

　　[7]李杰宇,代皓天浅析群智能优化算法的应用[J]科教导刊(电子版) , 2018(2):253.