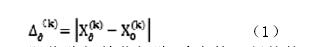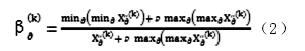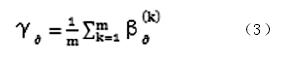问题的提出
20 世纪 90 年代中期以后,我国经济相继面临产业结构升级缓慢、消费市场低迷等问题,城镇化对产业结构升级的推动作用日益受到各界的重视。一般而言,城镇化的发展,依托于工业和服务业不断集聚所形成的产业支撑;与此同时,城市功能提升也为服务业发展提供了空间,而城镇化带来的农村居民身份转换,也会刺激其对教育、医疗、住房和社会保障等公共服务的相应需求。厘清服务业发展和城镇化之间的关系,继而推动二者在互动中快速、协同发展,对于正处于城镇化进程中、致力于推动产业结构调整的中国来说,是一个值得研究的课题。
国外较早研究城镇化与服务业关系的是 Chenery 和 Singlemann.Chenery(1975)提出随着城镇化进程的推进,服务业的重要性凸显,并将逐步取代替代工业成为推动城镇化进程的主要动力。Singelmann(1978) 通 过 对 1920-1970 年间工业化国家劳动力转移和产业结构变化的研究发现城镇化进程加快了农业型经济向服务业型经济转变,这是最早对城镇化进程能促进服务业发展的表述,为其后很多学者研究二者关系提供了分析框架。
郭克莎(2002)认为在城镇化推进过程中,城镇化早期和中期阶段工业发展对城镇化有较直接的带动作用,到了城镇化后期,在非农产业就业比重的增加中主导作用的是服务业就业比重及人数的增长。江小涓、李辉(2004)在研究服务业与中国经济发展的关系中发现,对服务业发展有着关键影响的因素是城市化水平提高。李程骅、郑琼洁(2012)基于江苏省域的经验数据,运用计量经济模型分析服务业与城镇化的动态关系,结果发现服务业对城镇化有正向促进作用,而城镇化尚未明显作用于服务业。近年灰色系统理论被广泛应用在各个领域,亦有不少学者运用灰色关联模型分析服务业与城镇化的关系,崔宏桥和沈颂东(2014)运用灰色关联分析吉林省城镇化与服务业各细分行业的关系,发现生活性服务业、公共服务业对吉林省城镇化有着较明显的推动作用,生产性服务业和休闲服务业对城镇化的推动效果有限。
目前对于城镇化与工业、服务业内在关系问题,无论是从产业结构演化角度还是服务业、工业直接与城镇化互动关系角度,地区内城镇化与服务业、工业之间有稳定的互动关系得到了学者们的公认。
在城镇化发展的初期,城镇化与工业的关系紧密,随着城镇化的不断推进,城镇化与服务业的关系逐渐显现。一般的,工业是城镇化水平提高的主要推动力,继工业化之后服务业则是推动城镇化的后续动力。本文基于区域经济发展异质性视角,以全国区域作为标准,选取北京市和河南省两个在经济发展水平与城镇化发展水平均存在较大差异的区域作为样本,研究服务业、工业与城镇化之间的关系,将二者进行对比分析以期发现不同发展水平的地区城镇化进程推动力的差异及其内在原因。
服务业、工业发展水平与城镇化关系的实证研究
(一)研究方法
因素分析的主要方法是回归分析,回归分析虽然是一种较常用的方法,但大都只用于少因素的、线性的。对于多因素的、非线性的则难以处理。考虑到回归分析方法的局限性和不足,灰色系统理论采用灰色关联模型来进行系统分析。作为一个发展变化的系统,关联度分析是动态过程发展态势的量化分析。由于工业、服务业的发展状况与城镇化水平之间的关系具有很大的不确定性,并且随着政策、经济等因素的变化,具有典型的灰色系统的特征精确的数理模型很难建立,故选用灰色关联模型较合适。灰色关联模型分析定量研究诸研究因素间相关性的强弱及次序,主要根据因素间发展趋势的相似程度。若系统中各因素在发展过程中的相对变化趋势大体一致,则认为二者关联度大,反之,则二者关联度小。主要分析步骤为:
1. 确定参考序列和比较序列。参考序列记作 X0,第 k 时刻的值为 X0(k)。因此,参考序列 X0可表示为 X0={X0(k),k是时间 }.比较序列,记作 X , =1、2…n,则第 k 时刻的值为 X (k)。因此,参考序列 X 可表示为 X ={ X (k),=1、2…n;k 是时间序列 }.
2. 对原始数据序列进行无量纲化处理,得到初始矩阵 X`.在分析时,各序列中的数据可能因量纲不同不便于比较,要去掉数据不同量纲对分析结果的影响。无量纲化的方法常用的有初值化、均值化与区间相对值化。
3. 计算离差序列。利用公式:
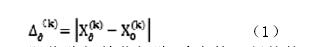
即将除初始化矩阵 X` 中第一行外的其他行与第一行做差,求出相对城镇化率的离差矩阵 X``.
4. 求参考序列与比较序列的关联系数。计算公式如下:
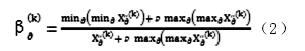
5. 求得关联度 γ 并进行排序。关联系数的数很多,过于分散,不便于分析比较其关联强度,故求各时间段关联系数的平均值,将其量化为一个比较集中的数值。其公式为:
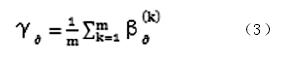
6. 求关联序。用关联度的次序及大小求因素间的关联度。将各因素关联度按大小顺序排列起来,便组成了关联序矩阵,记作 {μ}.
(二)服务业、工业发展水平与城镇化进程的灰色关联分析
根据灰色关联分析模型,本文选取2006-2013 年城镇化率作为参考序列记作:Xθ0,其中 θ=0 表示河南省,θ=1表示全国,θ=2 表示北京市,第 k 时刻的 值 为 Xθ0(k)。 因 此, 参 考 序 列 Xθ0,Xθ0={Xθ0(k),k=1、2、3…8,θ=0、1、2}.
以同期河南省、全国、北京市服务业生产总值占 GDP 的比重、工业生产总值占 GDP 的比重作为比较序列,记作 Yθ={ Yθ(k), =1、2;k=1、2、3…8,θ=0、1、2},其中 =1 表示服务业,=2 表示工业。
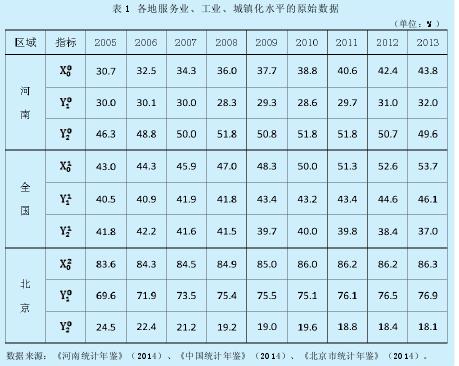
需要说明的是,因为经济数据多数呈稳定增长态势,为使增长趋势更加明显,保证分析结果的可靠性,常选用初值化处理。初值化就是所有数据均用第 1 个数据除,得到新矩阵。样本选择河南省、全国、北京市 2005-2013 年服务业、工业及城镇化的统计数据,原始数据整理如表 1 所示。
(三)实证结果及分析