0 引言
《高等数学》是高职院校课程体系中主要课程之一。近些年,随着社会经济的持续发展,社会科学、经理管理、工程技术、生命科学、自然科学等诸多专业领域都已成为高等数学的“用武之地”.但是严格来讲,高职教育系职业技术教育的分支,其课程教育旨在培养适合一线岗位的技能应用型职业人才。高等数学是一门基础理论课程,课程教学必须“以应用为目的,以必需够用为度”,必须“联系实际,深化概念,注重应用,重视创新,提高素质”,其教学任务主要是使学生掌握基础数学知识,提高其数学文化素养以及对数学基础知识的实际应用能力,通俗地讲就是能够运用所学的数学专业知识去解决实际问题,为就业上岗提供必备的数学基础。
1 背景
1.1 高职学生基本情况 俗话说,父母是孩子的第一个老师,笔者发现,有不少学生所接受的家庭教育都或多或少存在问题,家长急于望子成龙,教育孩子时态度粗暴,造成孩子的逆反心理或依赖心理。从高职学生总体的生源质量来看,学生素质偏低,教育情况令人堪忧。最近几年,随着高校扩招政策的推出,有许多学生擦着建档分数线入的学,他们的数学基础都不太不扎实,对知识的接受能力较差,尤其是对数学课程兴致索然,普遍缺乏学习的积极性,为了应付考试或者为了修学分而不得不学习,两极分化现象比较严重。
1.2 高职高等数学教学现状 随着我国教育改革的推进,对数学课程的要求有所提高,但是课时不增反减。面对校对的学习内容和有限的课时安排,一部分院校难于确定教学计划,为了完成教学任务,教师在设计教学计划时把重点放在完成教学进度上,一些需要精讲、细讲的题目一带而过,最后虽然完成了教学任务,教学质量却大打折扣。
教学过程缺少学生参与的双边活动,内容抽象难以掌握,一部分学生主观上有对学习数学有畏难情绪,兴趣缺失,学习态度不积极。这部分学生对数学的认识不深刻,认为学习数学就是学习一些计算技巧,在学习过程中普遍表现出“轻概念重计算”,根本不会运用数学所学去解决实际问题。此外,教师的教学观念陈旧,思想保守,方法单一,手段落后。目前,一些高等数学专业的教师虽然有丰富的理论知识,但也缺乏实际应用能力,教学内容未能很好地符合高职学生的特点。
2 适应专业需要,改革教学内容
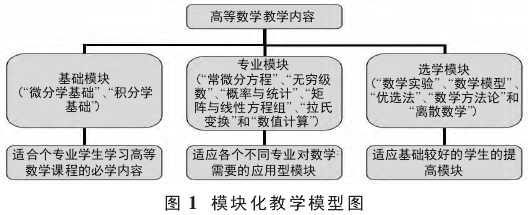
2.1 整合、优化课程体系,模块化教学 要做好高中教育与高职教育之间的衔接,专业课程的教学必须同步开展。教学内容应该侧重基础教育,同时富有一定弹性,使知识结构适应能力培养要求。“富有弹性”的教学模块应该这样设计:要根据专业需要编排教学内容和典型例题,至少涉猎到几个大类专业。教师在教学中可参考现实条件灵活筛选教学内容。具体来说,高职数学课程教学内容应该囊括图 1 所示的几个模块。
“基础模块”是高等数学课程教学中最重要的学习内容,该模块所囊括的都是各专业所需要的共性的知识内容,体现了高职专科数学素质教育、数学思维以及数学知识应用能力的教育要求。基础模块主要分为微分学基础和积分学基础两部分内容,将一元、多元微积分揉在一起进行学习,以节为单元模块在中学数学的基础上延伸出微积分,一般每节安排 2-4 学时和一次课后作业。
“专业模块”是“常微分方程”、“无穷级数”、“概率与统计”“、矩阵与线性方程组”、“拉氏变换”和“数值计算”六个模块的总和。该模式是为了适应各专业对数学的需求而设立的,因而教学内容(如理论知识、案例等内容)须由各专业课教师与数学教师共同编排,并且教学内容必须充分体现出数学知识的“应用性”.在授课过程中,教师的授课方式不一定局限于“填鸭式”理论灌输方式,可以更加灵活的选择实验室授课模式,也可以采用案例教学法,针对某一项技术问题逐步展开教学内容,中间穿插数学基础理论,帮助学生夯实基础。从专业模块的教学内容和教学方式来看,它应该属于跨学科的教学模式。这种全新的教学方式更有助于培养学生的独立思维方式和对知识的综合运用能力。从某些层面来讲,这种“理工结合、多学科交叉融合”的教学模式恰好迎合了当前社会上复合型、应用型的人才需求,对于培养学生的职业能力大有裨益。
针对有一定专业基础的学生开设“选学模块”,在该模块下以讲座形式分设“数学实验”、“数学模型”、“优选法”、“数学方法论”和“离散数学”五个小模块供学生选修。
2.2 注重内容的创新性,准去把握知识传授与能力培养的关系 围绕数学知识的“产生、解决和应用”准确把握继承与发展之间的关系。运用灵活的教学手段活化课程内容,摒弃以往“重定义、公式,轻知识运用”的生硬刻板的理论灌输方式,通过案例教学、实验教学充分阐明数学知识的由来和知识应用的最终目的。针对问题逐步展开教学主题,中间穿插数学史的基础知识,然后详细阐述对问题的处理方式,由此引出基础概念,介绍其来龙去脉,使学生对学习数学的目的有更客观、更充分的认识。在授课过程中穿插数学史内容,能够使学生更了解数学文化,这种理性教育能赋予学生特殊的思维品质,对提高学生的综合素质大有裨益,因此是数学课程中必不可少的内容。
2.3 注重理论与实际的联系 将数学知识与实际需要相结合,又将数学的理论与实际应用相联系。加大在案例教学方面做得比较出色,他们在教师中会侧重数学与实际生活,尤其是像传染病例分析、人口预测、死亡时间鉴定、物体逃逸地球的速度等与现代技术存在密切联系的典型案例,教学时应该尽量使学生对其应用方向有深刻的认识,这样更有利于培养学生对数学知识的综合运用能力。
3 教学方法的改革,实现培养目标
3.1 创设情境,激发兴趣 心理学研究表明,在轻松愉悦的学习环境中学生的学习效率最高。作为教师,在数学教学中应该有意识的为学生创设这样的学习氛围,使其在放松、明快的环境中自觉去探索数学的奥秘。
3.2 结合专业,讲清概念 由于一部分学生欠缺数学常规思维,教师在教授数学概念时,应该根据专业选择能够启发其数学思维的教学案例,课堂上要多鼓励其针对不同的问题或现象进行观察、对比,充分开拓其形象思维。另外,所选的数学案例应该与学生的专业有密切的联系,这样容易帮助其充分理解数学概念的内容和特征。在理解概念的基础上再进行分析与综合运用,从中概括出抽象的数学概念。比如在教授导数概念时,一方面要举出课本上变化率问题中介绍的变速直线运动的速度外,另一方面也要围绕专业特点穿插一些变化率问题,特别是机电类专业课程,应该适当穿插一些质量非均匀分布细杆的线密度、变速圆周运动的角速度、非恒定电流的电流强度等变化率问题。
3.3 减少推导,简化过程 高数课程教学切忌过度强调其严密性,应该根据生源的数学基础合理编排课程内容,培养模式也不应该局限于理论灌输。譬如讲求导的四则运算法则时,授课过程中可以只推导函数乘积的求导公式,就没必要逐一推导和、差、商的求导法则。而函数极值的必要条件、函数单调性定理,只需构造出典型的几何图形进行说明即可,没必要进行复杂的数学证明;在讲授极限的概念时,若采用刻板生硬的“ε-δ 语言进行阐释很难保证学生能够充分理解,建议教师转换成”趋向于“、”无限接近“”、越来越“等俗语进行讲解,这样能够更好的帮助学生消化这一概念。
3.4 运用工具,调动积极性 可以尝试将高职数学的教学与计算机功能相结合。比如定积分和二重积分的概念,可通过生动形象的动画进行阐释;积分、求导数、解微分方程、展开函数的幂级数等概念可通过专用的数学软件展开运算;运用数学软件绘制空间曲面、演示傅立叶级数的生成以及级数部分和逼近函数的情况等数学实验。实验教学的优势在于能够为学生创设一种参与式的学习情境,帮助其更直观的认识数学知识,同时培养学习兴趣,提高对数学知识的应用能力。
以往数学教学常采用以教师为中心的理论灌输式授课方式,教学进度、教学内容全部由教师一手主导,教与学严重脱节,在客观上压制了学生主观能动性的发挥。如今教师的角色发生了转变,在教学中教师不再是绝对的主导者,在授课过程中更多的是扮演辅助者、引导着的角色,对于教学方式、学习进度等学生拥有了更多的选择权,他们是数学课堂的参与者,在课程教学中发挥着主体作用。例如教师采用启发式授课方式就能够大大提高学生的积极性和主动性。在课堂上,每个主要知识都可用引问开始,鼓励学生独立思考问题,带着问题逐步深入学习;研究式教学模式有助于激发学生的求知欲,从而逐步培养起数学兴趣。在数学课教学中,教师可以灵活运用多种教学方法,比如通过创设情境来培养学生的独立思维能力。另外,在章节学习结束后,教师应该有意识的设置综合习题讨论课,引导学生独立思考综合运用数学知识去解决现实问题,在深入思考的基础上鼓励其互相交流,以调动课堂氛围,一改学生被动的学习格局。
4 结语
综上所述,随着高职学制的改革,高职数学对基础课中数学有了不同的要求,要成功实施模块化,想做好高等数学与各专业紧密结合,达到高职教育的教学目的,这就对我们高等数学老师提出了更高的要求。数学教师要对所教专业与数学的联系有较多的了解,充分了解各专业的发展对数学课的要求,掌握各专业所必备的数学知识;教学中做到相互渗透,同时掌握现代化的教学手段,熟练使用计算机及相关软件等,才能用数学自身的魅力唤起学生的学习热情,从而使学生感受到数学知识的丰富和有趣。
参考文献:
[1]王正萍,吴孝芹。高职高等数学教学改革研究与实践[J].科教广汇,2006,12.
[2]李小娥。高等数学教育创新模式的实践与探索[J].天津商务职业学院学报,2014(04)。
[3]王海菊。高等数学教育中存在的主要问题与改进措施[J].教育教学论坛,2013(20)。
[4]李春梅。高职院校高等数学教学现状分析及整改方案[J].中国培训,2016(14)。
[5]谷志元。高职数学课程教学改革之我见[J].职教论坛,2012(05)。