农业科学领域二重积分的运用

　　摘    要：　二重积分是高等数学的重要内容，有着广泛的应用范围。在数学领域中，它可以计算曲面的面积、证明不等式等；在物理学中，可利用二重积分求薄片的质量，转动惯量等。我们考虑二重积分在农业中的应用，从农业的角度给出二重积分的实用例子，从而拓宽学生们的知识视野。

　　关键词：　二重积分; 农业; 应用;

　　Abstract：　Double integral is an important part of higher mathematics and has a wide range of applications.In the field of mathematics,it can calculate the area of curved surface,and prove inequality.In physics,the mass and moment of inertia of thin sheet are calculated by double integral.In this paper,the application of double integral in agriculture is considered,and practical examples of double integral are given from the perspective of agriculture,so as to broaden students' knowledge horizons.

　　Keyword：　double integral; agriculture; application;

　　一、引言

　　作为农科类院校的一门重要基础课程，高等数学在培养适应新世纪社会主义现代化建设需要的高级农科专门人才的教育中意义重大。高等数学不仅是学生学习后续课程的重要基础课程，也是将来走出校门从事理论和实践工作的必备课程，更是培养学生良好的逻辑思维能力的重要途径[1]。教学和实践的结合，从学生的实践中寻找例子，让他们知道学习这门课程的专业应用[2]。从而更加清楚自己的学习，激发学生的兴趣，使学习高等数学变为一件更有意义的事情。

　　二重积分是高等数学中的重要内容，它上承接着定积分，下引出三重积分和曲线积分、曲面积分。它在几何、物理、经济学等多个科学都有极其广泛的应用[3,4]。在几何上，计算曲顶柱体体积，求曲面面积等应用[5]，在物理上，求平面薄片的质量，计算转动惯量等应用，在经济上，求解投资收益问题。本文从农业的角度，给出二重积分的实用例子，从而拓宽我们的知识视野。

　　二、二重积分在农业中的应用

　　（一）禾谷类的面积

　　根据田间试验统计方法测得，禾谷类每一张叶子以叶脉为x轴，叶尖端（原点）至最宽的边缘轨迹大体符合抛物线y2=Ax，而另一半从最宽处至叶基部分边缘轨迹是抛物线y2=A(B-x).

　　例1：一片稻叶叶尖沿叶脉至最宽处的距离是36厘米，最宽处的宽度是1.8厘米，叶子全长60厘米，叶基宽是1.2厘米。求该叶子的面积。
 

　　解：因叶缘轨迹大概是抛物线，将已知的点坐标（36,0.9）和（60,0.6）代入到如上分析的抛物线，则y12=0.0225x,y22=0.019(79.2-x）。叶面积是两个抛物线交的区域，则

　　故该叶子的面积是82.6厘米。

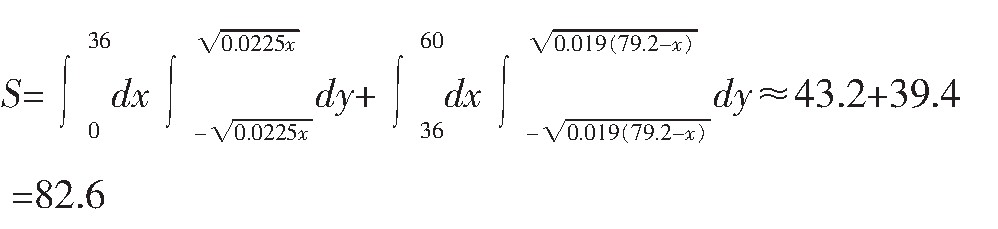
　　（二）果木冠状体积

　　根据极坐标系的二重积分，我们得到

　　例2：今测得某株柿子树的冠状体高度是4米，冠状体在底面的垂直投影半径是2.5米，锥体高是1米，求冠状体的体积。

　　解：根据冠状体的体积公式，得

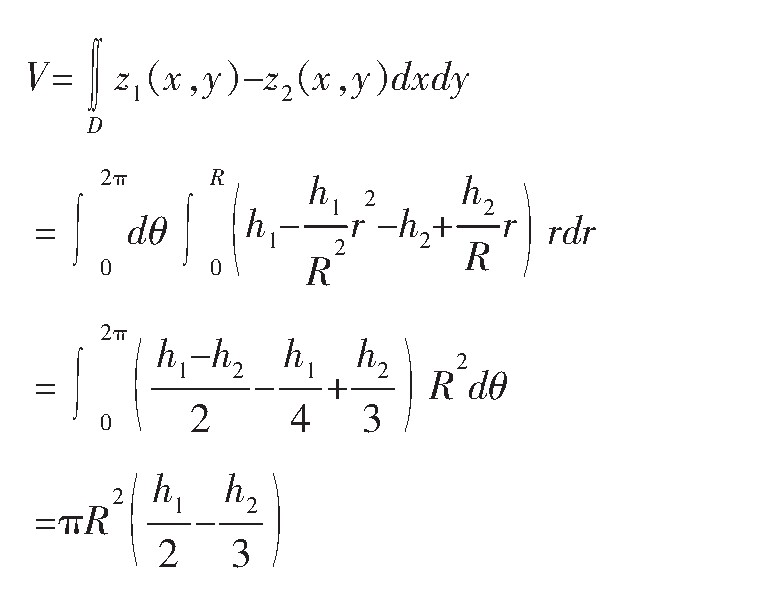
　　（三）作物叶子的光合作用

　　叶子在光照作用下产生叶绿素，向根系和主基输送营养成分。假定叶子的有效面在xoy平面上是一个闭区域，在某一定单位时间内，它在点（x,y）处的光合作用函数是f(x,y）≥0，那么整片叶子的叶绿素可用二重积分表示成

　　例3：设一片叶子占据的区域是D，其中关于y轴对称的一半区域D1由螺线乙上的一段弧与直线围成。在区域D上的光合作用函数是，求叶子在区域D上的叶绿素。

　　解：根据区域D关于y轴对称性和光合作用函数f(x,y)=f(-x,y）关于x是偶函数，得到在区域D上的叶绿素：

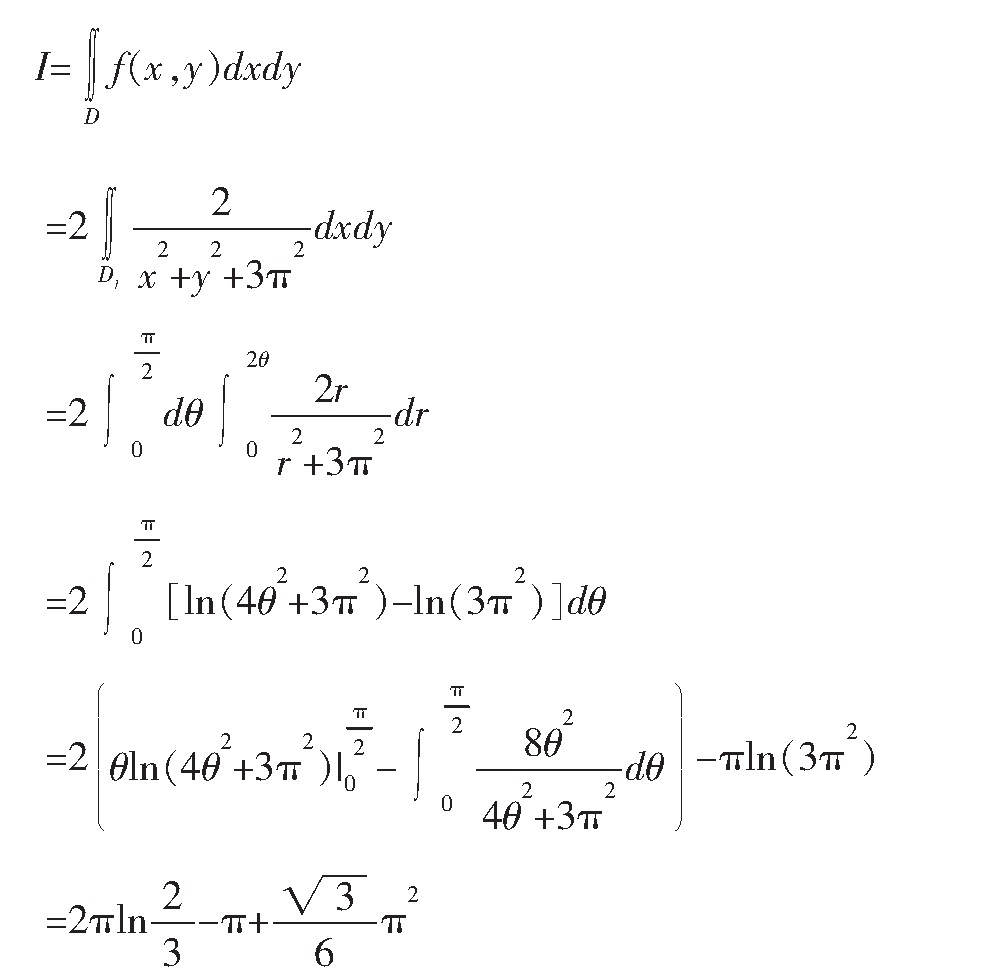
　　三、结语

　　通过以上的讨论，我们了解到二重积分是研究农业科学问题的一个有力工具。在今后的学习和日常活动中，我们需对二重积分做进一步理解和认识，让二重积分这个有力工具在我们农业院校中发挥更大的作用。

　　参考文献

　　[1]刘慧璋.农业高等数学教学存在的问题及其解决[J].农业信息网络,2011（10）.
　　[2]吕海燕,张丹,李海旺.农科高等数学教学方法探索[J].教育教学论坛,2014（3）.
　　[3]梁保松,王建平,陈振.高等数学[M].北京:中国农业出版社,2015.
　　[4]同济大学数学系.高等数学[M].北京:高等教育出版社,2014.
　　[5]郭运瑞.高等数学[M].北京:科学出版社,2012.